POJ 1417 True Liars

2023-10-31 18:41
文章标签 poj true liars 1417

本文主要是介绍POJ 1417 True Liars，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

POJ连炸多日……

题目

岛上有两种人，一种只说假话，一种只说真话。给出两种人的数量和一些你问他们的问题（问A，B是不是说真话），问是否能确定每个人到底是说真话还是说假话。

题解

1.发现a,b相同会回答yes 否则回答no

2.套用并查集模板 画图

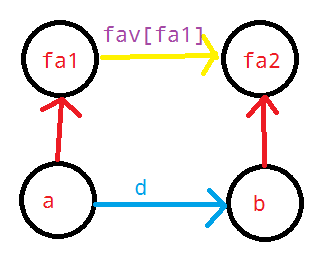
设边权：相同为0，不同为1

猜\(fav[fa1]=fav[a] \) xor \( fav[b] \;\) xor \( d\)，枚举各种情况果然成立……

3.得到一棵树

其实中途会进行路径压缩……

可以统计每棵树中与代表元素相同的个数(A[i])和不同的个数(B[i])（边权为1说明不同，为0说明相同）

然后问题就转换成

\(n = 树的棵数\)

\(X[i] = A[i]\;\;\;or\;\;\;B[i]\;\;\;\left( {1 \le i \le n} \right)\)

\(S[i] = \left\{ {\begin{array}{*{20}{c}}
{X[i]}&{i = 1}\\
{S[i - 1] + X[i]}&{2 \le i \le n}
\end{array}} \right.\)

 

问是否有且仅有1中选择方法使$S[n]=p1$

刚开始用暴力枚举$O(2^n)$ 一定超时……

犯的错误：

注意统计每棵树的时候有可能会错，如

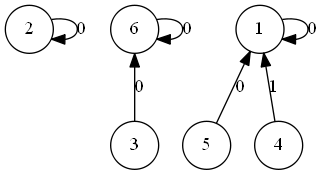
如果按照没有访问根节点就……

犯的错误

 

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<algorithm>
  4 #ifndef max
  5 #define max(a,b) ((a)>(b)?(a):(b))
  6 #endif
  7 #define REP(x,i,j) for(int x=i; x<j; x++)
  8 #define REPE(x,i,j) for(int x=i; x<=j; x++)
  9 #define MAXN 607
 10 using namespace std;
 11 int fa[MAXN];
 12 int fav[MAXN];
 13 int n,p,q;
 14 inline void initu() {
 15     REPE(i,0,n) {
 16         fa[i]=i;
 17         fav[i]=0;
 18     }
 19 }
 20 
 21 inline int findu(int x) {
 22     int t=x, p;
 23     int v=0,vt;
 24     while(t!=fa[t]) {
 25         v^=fav[t];
 26         t=fa[t];
 27     }
 28     while(x!=t) {
 29         vt =v;
 30         p=fa[x];
 31         fa[x]=t;
 32         v^=fav[x];
 33         fav[x]=vt;
 34         x=p;
 35     }
 36     return t;
 37 }
 38 
 39 //inline void uu(int x, int y, int d) {
 40 //    int a=findu(x), b=findu(y);
 41 //    int va=fav[x], vb=fav[y];
 42 //    fa[a]=b;
 43 //    fav[a]=va^vb^d;
 44 //}
 45 
 46 int main() {
 47     int a;
 48     while(~scanf("%d%d%d", &a, &p, &q) && (a || p || q)) {
 49         n=p+q;
 50         initu();
 51         REP(i,0,a) {
 52             int x,y;
 53             char s[4];
 54             scanf("%d%d%s", &x, &y, s);
 55             bool d = s[0]=='n';
 56             int a=findu(x), b=findu(y);
 57             if(a!=b) {
 58                 fa[a]=b;
 59                 fav[a]=fav[x]^fav[y]^d;
 60             }
 61         }
 62         if(p==q) {
 63             printf("no\n");
 64         } else {
 65             bool gen[MAXN]; memset(gen,0,sizeof gen);
 66             int cnt[MAXN][2]; memset(cnt,0,sizeof cnt);
 67             int dp[MAXN][MAXN]; memset(dp,0,sizeof dp);
 68             int cntgen[MAXN]; memset(cntgen,0,sizeof cntgen);
 69             dp[0][0]=1;
 70             int ki = 0;
 71             REPE(i,1,n) {
 72                 int t = findu(i);
 73                 if(!gen[t]){ki++;gen[t]=true;cntgen[ki]=t;}
 74                 cnt[ki][fav[i]]++;
 75             }
 76             REPE(i,1,ki){
 77                 for(int j=p;j>=0;j--){
 78                     if(j-cnt[i][0]>=0&&dp[i-1][j-cnt[i][0]]){
 79                         dp[i][j]+=dp[i-1][j-cnt[i][0]];
 80                     }
 81                     if(j-cnt[i][1]>=0&&dp[i-1][j-cnt[i][1]]){
 82                         dp[i][j]+=dp[i-1][j-cnt[i][1]];
 83                     }
 84                 }
 85             }
 86             if(dp[ki][p]!=1) {
 87                 printf("no\n");
 88                 continue;
 89             } else {
 90                 int ansarr[MAXN], ansarri = 0; memset(ansarr,0,sizeof ansarr);
 91                 for(int i=ki;i>=1;i--) {
 92                     if(p-cnt[i][0]>=0&&dp[i-1][p-cnt[i][0]]){
 93                         for(int j=1;j<=n;j++){
 94                             if(fa[j]==cntgen[i]&&fav[j]==0)ansarr[ansarri++]=j;
 95                         }
 96                         p-=cnt[i][0];
 97                     } else {
 98                         for(int j=1;j<=n;j++){
 99                             if(fa[j]==cntgen[i]&&fav[j]==1)ansarr[ansarri++]=j;
100                         }
101                         p-=cnt[i][1];
102                     }
103                 }
104                 sort(ansarr,ansarr+ansarri);
105                 REP(i,0,ansarri) {
106                     printf("%d\n", ansarr[i]);
107                 }
108                 printf("end\n");
109             }
110         }
111     }
112     return 0;
113 }
WA代码

 

后来抄了个DP，还不知道怎么分析:(

还得多练DP:(

设dp[i][j]为前i组人中说真话的人数为j这种情况的数量，很容易写出转移方程

然后倒过来输出解（因为要判断到底是怎么转移过来的）

 

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<algorithm>
  4 #include<map>
  5 #ifndef max
  6 #define max(a,b) ((a)>(b)?(a):(b))
  7 #endif
  8 #define REP(x,i,j) for(int x=i; x<j; x++)
  9 #define REPE(x,i,j) for(int x=i; x<=j; x++)
 10 #define MAXN 1007
 11 using namespace std;
 12 int fa[MAXN];
 13 int fav[MAXN];
 14 int n,p,q;
 15 
 16 bool gen[MAXN];      
 17 int cnt[MAXN][2];    
 18 int dp[MAXN][MAXN];  
 19 int cntgen[MAXN];    
 20 map<int,int> kitogen;
 21 inline void initu() {
 22     REPE(i,0,n) {
 23         fa[i]=i;
 24         fav[i]=0;
 25     }
 26 }
 27 
 28 inline int findu(int x) {
 29     int t=x, p;
 30     int v=0,vt;
 31     while(t!=fa[t]) {
 32         v^=fav[t];
 33         t=fa[t];
 34     }
 35     while(x!=t) {
 36         vt =v;
 37         p=fa[x];
 38         fa[x]=t;
 39         v^=fav[x];
 40         fav[x]=vt;
 41         x=p;
 42     }
 43     return t;
 44 }
 45 
 46 //inline void uu(int x, int y, int d) {
 47 //    int a=findu(x), b=findu(y);
 48 //    int va=fav[x], vb=fav[y];
 49 //    fa[a]=b;
 50 //    fav[a]=va^vb^d;
 51 //}
 52 
 53 int main() {
 54     int a;
 55     while(~scanf("%d%d%d", &a, &p, &q) && (a || p || q)) {
 56         n=p+q;
 57         initu();
 58         memset(gen,0,sizeof gen);      
 59         memset(cnt,0,sizeof cnt);      
 60         memset(dp,0,sizeof dp);        
 61         memset(cntgen,0,sizeof cntgen);
 62         kitogen.clear();
 63         REP(i,0,a) {
 64             int x,y;
 65             char s[4];
 66             scanf("%d%d%s", &x, &y, s);
 67             bool d = s[0]=='n';
 68             int a=findu(x), b=findu(y);
 69             if(a!=b) {
 70                 fa[a]=b;
 71                 fav[a]=fav[x]^fav[y]^d;
 72             }
 73         }
 74         if(p==q) {
 75             printf("no\n");
 76             continue;
 77         } else {
 78             dp[0][0]=1;
 79             int ki = 0;
 80             REPE(i,1,n) {
 81                 int t = findu(i);
 82                 if(!gen[t]){ki++;gen[t]=true;cntgen[ki]=t;kitogen[t]=ki;}
 83                 cnt[kitogen[t]][fav[i]]++;
 84             }
 85 //            #define DBG(x,...) printf(x, ##__VA_ARGS__)
 86 //            REPE(i,1,ki) {
 87 //                DBG("%d: %d, %d @%d\n", i, cnt[i][0], cnt[i][1], cntgen[i]);
 88 //            }
 89             REPE(i,1,ki){
 90                 for(int j=p;j>=0;j--){
 91                     if(j-cnt[i][0]>=0){
 92                         dp[i][j]+=dp[i-1][j-cnt[i][0]];
 93                     }
 94                     if(j-cnt[i][1]>=0){
 95                         dp[i][j]+=dp[i-1][j-cnt[i][1]];
 96                     }
 97                 }
 98             }
 99             if(dp[ki][p]!=1) {
100                 printf("no\n");
101                 continue;
102             } else {
103                 int ansarr[MAXN], ansarri = 0; memset(ansarr,0,sizeof ansarr);
104                 for(int i=ki;i>=1;i--) {
105                     if(p-cnt[i][0]>=0&&dp[i-1][p-cnt[i][0]]){
106                         for(int j=1;j<=n;j++){
107                             if(fa[j]==cntgen[i]&&fav[j]==0)ansarr[ansarri++]=j;
108                         }
109                         p-=cnt[i][0];
110                     } else if(p-cnt[i][1]>=0&&dp[i-1][p-cnt[i][1]]){
111                         for(int j=1;j<=n;j++){
112                             if(fa[j]==cntgen[i]&&fav[j]==1)ansarr[ansarri++]=j;
113                         }
114                         p-=cnt[i][1];
115                     }
116                 }
117                 sort(ansarr,ansarr+ansarri);
118                 REP(i,0,ansarri) {
119                     printf("%d\n", ansarr[i]);
120                 }
121                 printf("end\n");
122             }
123         }
124     }
125     return 0;
126 }
AC代码

 

转载于:https://www.cnblogs.com/sahdsg/p/10356873.html

这篇关于POJ 1417 True Liars的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/317336。

相关文章

poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

求一段字符串中的最长回文串。 因为数据量比较大，用原来的O（n^2）会爆。 小白上的O(n^2)解法代码：TLE啦~ #include<stdio.h>#include<string.h>const int Maxn = 1000000;char s[Maxn];int main(){char e[] = {"END"};while(scanf("%s", s) != EO
阅读更多...
hdu 2602 and poj 3624(01背包)

hdu 2602 and poj 3624(01背包)

01背包的模板题。 hdu2602代码： #include<stdio.h>#include<string.h>const int MaxN = 1001;int max(int a, int b){return a > b ? a : b;}int w[MaxN];int v[MaxN];int dp[MaxN];int main(){int T;int N, V;s
阅读更多...
poj 1511 Invitation Cards(spfa最短路)

poj 1511 Invitation Cards(spfa最短路)

题意是给你点与点之间的距离，求来回到点1的最短路中的边权和。 因为边很大，不能用原来的dijkstra什么的，所以用spfa来做。并且注意要用long long int 来存储。 稍微改了一下学长的模板。 stack stl 实现代码： #include<stdio.h>#include<stack>using namespace std;const int M
阅读更多...
poj 3259 uva 558 Wormholes(bellman最短路负权回路判断)

poj 3259 uva 558 Wormholes(bellman最短路负权回路判断)

poj 3259： 题意：John的农场里n块地，m条路连接两块地，w个虫洞，虫洞是一条单向路，不但会把你传送到目的地，而且时间会倒退Ts。 任务是求你会不会在从某块地出发后又回来，看到了离开之前的自己。 判断树中是否存在负权回路就ok了。 bellman代码： #include<stdio.h>const int MaxN = 501;//农场数const int
阅读更多...
poj 1258 Agri-Net（最小生成树模板代码）

poj 1258 Agri-Net（最小生成树模板代码）

感觉用这题来当模板更适合。 题意就是给你邻接矩阵求最小生成树啦。~ prim代码：效率很高。172k...0ms。 #include<stdio.h>#include<algorithm>using namespace std;const int MaxN = 101;const int INF = 0x3f3f3f3f;int g[MaxN][MaxN];int n
阅读更多...
poj 1287 Networking（prim or kruscal最小生成树）

poj 1287 Networking（prim or kruscal最小生成树）

题意给你点与点间距离，求最小生成树。 注意点是，两点之间可能有不同的路，输入的时候选择最小的，和之前有道最短路WA的题目类似。 prim代码： #include<stdio.h>const int MaxN = 51;const int INF = 0x3f3f3f3f;int g[MaxN][MaxN];int P;int prim(){bool vis[MaxN];
阅读更多...
poj 2349 Arctic Network uva 10369（prim or kruscal最小生成树）

poj 2349 Arctic Network uva 10369（prim or kruscal最小生成树）

题目很麻烦，因为不熟悉最小生成树的算法调试了好久。 感觉网上的题目解释都没说得很清楚，不适合新手。自己写一个。 题意：给你点的坐标，然后两点间可以有两种方式来通信：第一种是卫星通信，第二种是无线电通信。 卫星通信：任何两个有卫星频道的点间都可以直接建立连接，与点间的距离无关； 无线电通信：两个点之间的距离不能超过D，无线电收发器的功率越大，D越大，越昂贵。 计算无线电收发器D
阅读更多...
poj 1502 MPI Maelstrom（单源最短路dijkstra）

poj 1502 MPI Maelstrom（单源最短路dijkstra）

题目真是长得头疼，好多生词，给跪。 没啥好说的，英语大水逼。 借助字典尝试翻译了一下，水逼直译求不喷 Description： BIT他们的超级计算机最近交货了。（定语秀了一堆词汇那就省略吧再见） Valentine McKee的研究顾问Jack Swigert，要她来测试一下这个系统。 Valentine告诉Swigert：“因为阿波罗是一个分布式共享内存的机器，所以它的内存访问
阅读更多...
uva 10061 How many zero's and how many digits ?（不同进制阶乘末尾几个0）+poj 1401

uva 10061 How many zero's and how many digits ?（不同进制阶乘末尾几个0）+poj 1401

题意是求在base进制下的 n！的结果有几位数，末尾有几个0。 想起刚开始的时候做的一道10进制下的n阶乘末尾有几个零，以及之前有做过的一道n阶乘的位数。 当时都是在10进制下的。 10进制下的做法是： 1. n阶位数：直接 lg（n！）就是得数的位数。 2. n阶末尾0的个数：由于2 * 5 将会在得数中以0的形式存在，所以计算2或者计算5，由于因子中出现5必然出现2，所以直接一
阅读更多...
poj 3159 （spfa差分约束最短路） poj 1201

poj 3159 （spfa差分约束最短路） poj 1201

poj 3159: 题意： 每次给出b比a多不多于c个糖果，求n最多比1多多少个糖果。 解析： 差分约束。 这个博客讲差分约束讲的比较好： http://www.cnblogs.com/void/archive/2011/08/26/2153928.html 套个spfa。 代码： #include <iostream>#include <cstdio>#i
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2