洛谷 P2437 蜜蜂路线 C++ （高精度）题解

题目背景

无

题目描述

一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 mm 开始爬到蜂房 nn，m<nm<n，有多少种爬行路线？（备注：题面有误，右上角应为 n-1n−1）

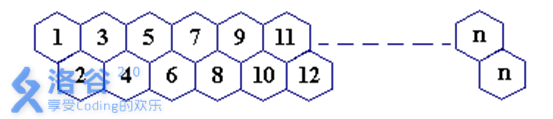
输入格式

输入 m,n 的值

输出格式

爬行有多少种路线

输入输出样例

输入 #1复制

1 14

输出 #1复制

377

说明/提示

对于100%的数据 M,N≤1000

 思路简介：

如果接触多了此类题就会很快的意识到，这肯定是存在规律或者递推式的。如果再对数学敏感一些，会很容易发现从任意一点m到m+1和m+2点的方法都是只有一种。所以不难想到，从任何一点m到另一点n的方法，就等于从m点到n-1的方法+到n-2点的方法。即f[m][n]=f[m]n-1]+f[m][n-2]。

这显然就是斐波那契数列的变式，关键就是怎么将题转化为斐波那契数列的解法。

既然已经确定了递推式，我们可以通过不完全归纳法和特解法来得到答案。

先穷举一部分斐波那契数列，1、1、2、3、5、8、13...

再穷举，当m等于1时候，n依次取值，分析结果，对比和斐波那契数列特殊项对应。发现n=2、3、4、5、6、7的结果，分别对应斐波那契数列第2、3、4、5、6、7项的结果。也可以取m=2，n依次取来验证。所以显然m和n确定的斐波那契数列项数便是第n-m+1项，从而用高精度轻易AC。

高精度AC代码如下：

#include<iostream>
using namespace std;
#define MAX 9999
int f[1001][MAX];
int len;
void fun(int x) {//高精度加法for (int i = 0; i < len; i++) {f[x][i] += f[x - 1][i] + f[x - 2][i];//递推式if (f[x][i] > 9) {f[x][i + 1]++;f[x][i] -= 10;}if (i == len - 1 && f[x][len])len++;}
}
int main(){int m, n;cin >> m >> n;f[1][0] = 1;//斐波那契数列前两项都是1f[2][0] = 1;len = 1;int x = n - m + 1;for (int i = 3; i <=x; i++) {fun(i);
}while (f[x][len - 1] == 0 && len > 1)len--;for (int i = len-1; i >=0; i--)cout << f[x][i];return 0;
}

当然此题也可以利用结构体模拟大整数类，利用运算符重载，快速幂，结合高精度运算等等来解决。话不多说，直接送上神犇的代码。

//本题其实就是求斐波那切数列的第n-m+1项，但由于数据过大，所以需要使用到高精度加法
#include<cstdio>
#include<cstring>	//strlen和memset所需头文件
#include<algorithm>	//reverse所需头文件
#define r register int	//register关键字将变量存储在CPU寄存器中，可以提高效率
struct BigInteger{char str[100001];	//str数组用于存储字符串int num[100001],len;	//num数组为str数组转为int类型的结果，len为str的长度，也就是num的大小inline void output(){	//输出函数，由于是反向模拟加法的，所以也需要反向输出for(r i=len-1;i+1;--i)printf("%d",num[i]);}BigInteger operator+(BigInteger &k){	//开始重载了，加法竖式模拟也不需要多解释len=max(len,k.len);r f=0;for(r i=0;i^len;++i){num[i]+=k.num[i]+f;if(num[i]>9)num[i]-=10,f=1;else f=0;}if(f)num[len++]=1;	//这里是对进位的处理return *this;	//*this返回一个指向类本身的指针}BigInteger(){	//初始化，清零所有变量和数组len=0;memset(str,0,sizeof str);memset(num,0,sizeof num);}BigInteger(int k){	//将BigInteger类型赋为int类型，也可当做强制转换使用memset(str,0,sizeof str);sprintf(str,"%d",k);	//sprintf与printf类似，可以当做将数值打印到字符串中，具体用法请自行度娘（笑）len=strlen(str);	//保存字符串长度std::reverse(str,str+len);	//由于需要反向模拟竖式，所以我们在这里就调用STL的reverse函数将str字符串倒过来for(r i=0;i^len;++i)num[i]=str[i]-48;	//将字符串转为int类型}
};
main(){BigInteger n(1),m(1);	//注意，这里必须初始化为1，否则会出错int a,b,c;scanf("%d%d",&a,&b);c=b-a+1;	//求出是求斐波那切数列的第几项for(r i=1;i^c;++i)	//这里的位运算其实优（zhi）化（shi）意（wei）义（le）不（zhuang）大（bi）if(i&1)n=n+m;	//这里的a^b可当做a<b或a!=b使用,c&1相当于c%2else m=m+n;if(c&1)n.output();	//注意这里，如果c为奇数，我们应该输出n（不是题意中的n！）else m.output();	//反之则c为偶数，我们应该输出m（不是题意中的m！）
}

总之，此题虽然在递归题单里，在数据量不大的时候显然用递归很容易。但此处显然是要利用高精的，所以还是那句话，刷题只要能把题AC和学习到相应的知识就行，而并不在于秀自己的编程技巧。