农场派对题解

本文主要是介绍农场派对题解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

农场派对

---

题目描述
寒假到了，N头牛都要去参加一场在编号为X（1≤X≤N）的牛的农场举行的派对（1≤N≤1000），农场之间有M（1≤M≤100000）条有向路，每条路长Ti（1≤Ti≤100）。
每头牛参加完派对后都必须回家，无论是去参加派对还是回家，每头牛都会选择最短路径，求这N头牛的最短路径（一个来回）中最长的一条路径长度。
输入
第一行三个整数N，M, X；
第二行到第M+1行：每行有三个整数Ai，Bi, Ti ,表示有一条从Ai农场到Bi农场的道路，长度为Ti。

输出
一个整数，表示最长的最短路得长度。

样例输入

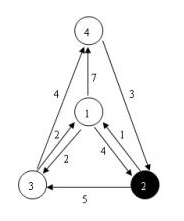
4 8 2
1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3

样例输出

10

---

这是一道最短路问题，可以用Dijkstra、spfa等方法来做

题中除了编号为X的牛以外每头牛有两个动作：1.去参加派对，2.回家。

spfa算法可以找到从一个点出发到其他点的最短距离，这可以解决题目中所要求的 参加派对 的操作，那如何解决 回家 的要求呢？
我们可以使用建立反向图来解决问题（例如将3→4建图建成4→3），建立完反向图再跑一遍spfa就能求编号X的点到其他点的最短距离，这不就是我们想要的 回家 操作吗？

总结一下就是用正向图跑一遍spfa求出除了X牛的各个牛参加派对的最短距离，再用反向图跑一遍spfa求出除了X牛的各个牛回家的最短距离，相加就能找出答案啦。

---

下面是代码

#include<bits/stdc++.h>
using namespace std;struct edge
{int v,w;
};
vector<edge>e[3][1010];//动态数组存边 
queue<int>q;//队列 
int n,m,l,f[3][1010],ans;//f数组表示在正向图和反向图中终点到各点最短距离
bool vis[1010];//vis数组表示各点是否在队列中 void spfa(int k)//k=1时正向图，k=2时反向图 
{memset(vis,0,sizeof vis);//初始化false vis[l]=true;f[k][l]=0;q.push(l);while(!q.empty()){int now=q.front();q.pop();vis[now]=false;for(int i=0;i<e[k][now].size();i++)//遍历从now点出发的各边 {int v=e[k][now][i].v,w=e[k][now][i].w;if(f[k][v]>f[k][now]+w){f[k][v]=f[k][now]+w;if(!vis[v]){vis[v]=true;q.push(v);}}}}
}int main(){cin>>n>>m>>l;memset(f,0x3f3f3f,sizeof f);for(int i=1;i<=m;i++){int u,v,w;scanf("%d %d %d",&u,&v,&w);edge cmp;cmp.v=v;cmp.w=w;e[1][u].push_back(cmp);//存正向图 cmp.v=u;e[2][v].push_back(cmp);//存反向图 }spfa(1);//跑正向图 spfa(2);//跑反向图 for(int i=1;i<=n;i++){//if(i==l)continue;ans=max(f[1][i]+f[2][i],ans);//找最长的 }cout<<ans;return 0;
}

这篇关于农场派对题解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---