2021年全国硕士研究生入学统一考试管理类专业学位联考数学试题——纯题目版

2021 年 1 月份管综初数真题

一、问题求解（本大题共 5 小题，每小题 3 分，共 45 分）下列每题给出 5 个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

1.某便利店第一天售出50种商品，第二天售出45种，第三天售出60种，前两天售出有25种相同，后两天售出商品有30种相同，这三天售出商品至少有( )种.
A.70
B.75
C.80
D.85
E.100

2.三位年轻人的年龄成等差数列，且最大与最小的两人年龄差的10倍是另一人的年龄，则三人中年龄最大的是( ).
A.19
B.20
C.21
D.22
E.23

3.$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{99}+\sqrt{100}}=（）$
A.9
B.10
C.11
D.$3\sqrt{11}-1$
E.$3\sqrt{11}$

4.设p，q是小于10的质数，则满足条件1<$\frac{q}{p}$<2的p，q有( ).
A.2组
B.3组
C.4组
D.5组
E.6 组

5.设二次函数$f(x)=a{x}^2+bx+c$且f(2)=f(0)，则$\frac{f(3)-f(2)}{f(2)-f(1)}=（）$.
A.2
B.3
C.4
D.5
E.6

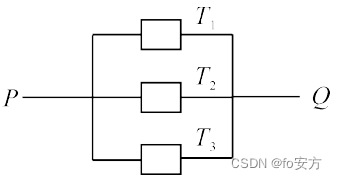
6.如图，由P到Q电路中有三个元件，分别为T， ，T，，T， ，电流能通过T)，T，，T5概率分别为0.9，0.9，0.99.假设电流能否通过三个元件相互独立，则电流能在P.Q之间通过的概率是().
A.0.8019
B.0.9989
C.0.999
D.0.9999
E.0.99999

7.若球体的内接正方体的体积为8m3，则该球体的表面积为( )$m^2$?.
A.4π
B.6π
C.8π
D.12π
E.24π

8.甲.乙两组同学中，甲组有3男3女，乙组有4男2女，从甲、乙两组中各选出2名同学，这4人中恰有1女的选法有( )种.
A.26
B.54
C.70
D.78
E.105

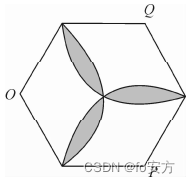
9.如图，正六边形边长为1，分别以正六边形的顶点О、P.Q为圆心，以1为半径作圆弧，则阴影部分的面积为( ).
A.$\pi -\frac{3\sqrt{3}}{2}$
B.$\pi -\frac{3\sqrt{3}}{4}$
C.$\frac{\pi }{2}-\frac{3\sqrt{3}}{4}$
D.$\frac{\pi }{2}-\frac{3\sqrt{3}}{8}$
E.$2\pi -3\sqrt{3}$

10.已知ABCD是圆$x^2+y^2=25$的内接四边形，若A，C是直线x =3与圆$x^2+y^2=25$的交点，则四边形ABCD面积的最大值为( ).
A.20
B.24
C.40
D.48
E.80

11.某商场利用抽奖方式促销，100个奖券中设有3个一等奖，7个二等奖，则一等奖先于二等奖抽完的概率为( ).
A.0.3
B.0.5
C.0.6
D.0.7
E.0.73

12.现有甲，乙两种浓度酒精，已知用10升甲酒精和12升乙酒精可以配成浓度为70%的酒精，用20升甲酒精和8升乙酒精可以配成浓度为80%的酒精，则甲酒精的浓度为( ).
A.72%
B.80%
C.84%
D.88%
E.91%

13.函数$f(x)=x^2-4x-2|x-2|$的最小值为().
A.-4
B.-5
C.-6
D.-7
E.-8

14.从装有1个红球，2个白球，3个黑球的袋中随机取出3个球，则这3个球的颜色至多有两种的概率（ ）
A.0.3
B.0.4
C.0.5
D.0.6
E.0.7

15.甲，乙两人相距330千米，他们驾车同时出发，经过2小时相遇，甲继续行驶2小时24分钟后到达乙的出发地，则乙的车速为().
A.70km/h
B.75km/h
C.80km/h
D.90km/h
E.96km/h

二.条件充分性判断:第16~25小题，每小题3分，共30分.要求判断每题给出的条件( 1)
和条件(2)能否充分支持题干所陈述的结论.A、B、C、D、E五个选项为判断结果，请选择一项符合试题要求的判断.
A:条件( 1)充分，但条件(2)不充分.
B:条件(2)充分，但条件( 1)不充分.
C:条件(1)和(2)单独都不充分，但条件(1)和条件(2)联合起来充分.
D:条件(1)充分，条件(2)也充分.
E:条件(1)和(2)单独都不充分，条件( 1)和条件(2)联合起来也不充分.

16.某班增加两名同学.则该班同学的平均身高增加了.
（1）增加的两名同学的平均身高与原来男同学的平均身高相同.
（2）原来男同学的平均身高大于女同学的平均身高.

17.清理一块场地，则甲乙丙三人能在2天内完成.
（1）甲乙两人需要3天完成.
（2）甲丙两人需要4天完成.

18.某单位进行投票表决，已知该单位的男女员工人数之比为3:2，则能确定是至少有50%的女员工参加
了投票.
（1）赞成投票的人数超过了总人数的40% .
（2）参加投票的女员工比男员工多.

19.设a，b为实数，则能确定lal +lbl的值.
（1）已知la+bl的值.
（2）已知la -bl的值.

20.设a为实数，圆C:$x^2+y^2=ax+ay$，则能确定圆C的方程.
（1）直线x +y=1 与圆C相切.
（2）直线x-y =1与圆C相切.

21.设x ，y为实数，则能确定x≤y.
（1）$x^2\le y-1$.
（2）$x^2+(y-2{)}^2\le 2$.

22.某人购买了果汁、牛奶、咖啡三种物品，已知果汁每瓶12元，牛奶每瓶15元，咖啡每盒35元，则能确
定所买各种物品的数量.
（1）总花费为104元.
（2）总花费为215元.

23.某人开车去上班，有一段路因维修限速通行，则可以算出此人上班的距离.
（1）路上比平时多用了半小时.
（2）已知维修路段的通行速度.

24.已知数列{a}，则数列{a}为等比数列.
（1）$a_n{a}_{n+1}＞0$.
（2）$a_{n+1}^2-2a_n^2-a_n{a}_{n+1}=0$.

25.给定两个直角三角形，则这两个直角三角形相似.
（1）每个直角三角形边长成等比数列.
（2）每个直角三角形边长成等差数列.

参考答案
1-5 BCABB
6-10 DDDAC
11 -15 DEBED
16-20 CECCA
21 -25 DAECD