利用numpy实现GCNs的传递过程实例

0.引言

CNN能够对欧式空间结构的数据进行处理，但无法很好的处理非欧式空间结构的数据，例如知识图谱、社交关系、生物分子结构等。而2016年提出的图卷积网络（Graph Convolutional Networks, GCNs），则可以很好的处理这些数据，并能够取得很好的效果。本文将利用numpy实现一个简易的图卷积网络，进而展示GCN如何从上一层聚集信息，以及该机制如何在图中生成有用的节点特征表示。

注意：如果没有任何GCNs的基础，建议在阅读本文之前，先阅读GCNs介绍

1.再谈GCNs

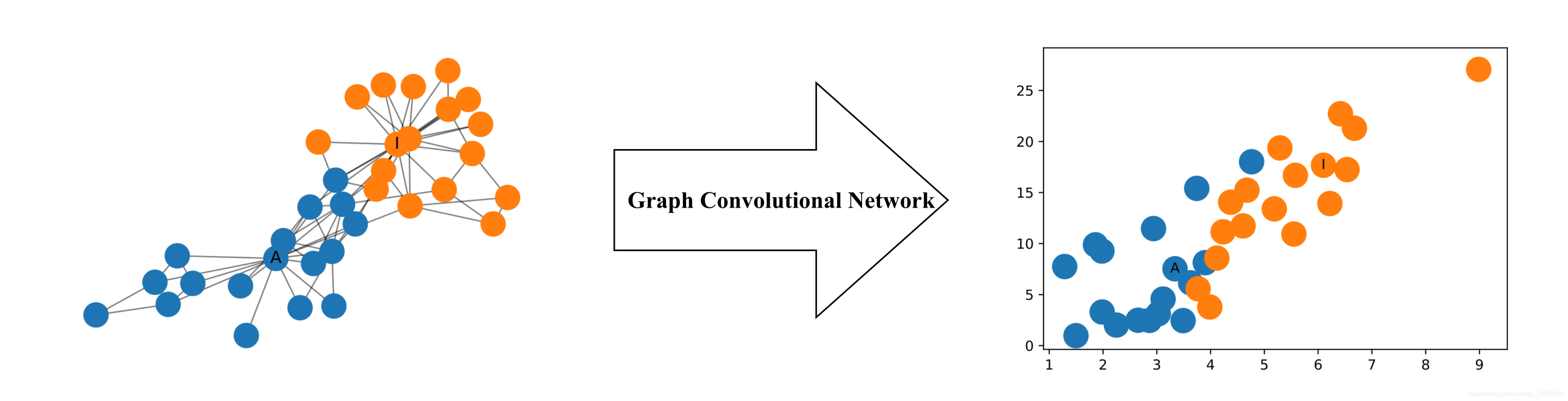
在机器学习中，GCNs是近几年来比较热门的模型，原论文来源于Semi-Supervised Classification with Graph Convolutional Networks。如下图所示，即使是两层的GCNs，其生成的每个节点的二维表征，即使没有经过任何模型的训练，这些二维表征也能够展示出图中节点的相对邻近性的特性。

对于图$G=(V,E)$，我们考虑以下两个量：

• 考虑$G$的特征矩阵$X$。我们令$X$的维度为$N\times D$（$N$表示节点的数量，$D$表示输入特征的数量）
• 考虑$G$的邻接矩阵$A$。我们令$A$的维度为$N\times N$（$N$表示节点的数量）

GCNs的目标是，构建一个非线性函数的映射关系式，这个关系式（或者说网络模型）能够输入$N\times D$维度的特征矩阵$H$，以及$N\times N$维度的邻接矩阵$A$，输出$N\times F$维度的特征矩阵$Z$。按照较为我们熟知的普遍的全连接神经网络的思路，我们定义这个关系式（网络模型）有多层的非线性函数表示，那么有
$$H^{(l)}=f(H^{(l-1)},A)$$
其中，$l=1,2,...,L，H^{(0)}=X，H^{(L)}=Z$（$z$表示节点级输出），$H$表示特征矩阵，$L$表示层数。需要注意的是，对于第$l$层的$H$（也就是第$l$层的特征矩阵），其维度为$N\times M^{(l)}$，那么$M^{(0)}=D，M^{(L)}=F$，该矩阵的行，表示单个节点的特征表示。而具体的模型，差异在如何对$ f(⋅,⋅)$进行选择和对其进行参数化。表示一种可自定义的传播规则，实际上就是一种非线性激活函数，一般采用例如$ReLU、tanh、Sigmoid$等激活函数。也就是说，在每一层，可以利用传播规则$f$将这些特征聚合（激活）成下一层的特征。通过这种方式，我们从CNN对图像特征提取的思路类比就可以发现，越往后面的层，那么其特征表示的信息就会越来越抽象。

现在，假定$f$的传播规则如下所示：
$$f(H^{(l)},A)=\sigma (A{H}^l{W}^l)$$
其中，$\sigma$是一种非线性激活函数，例如$ReLU$，而$W^l$表示第$l$层的权重，则$W^l$的维度为$M^{(l)}\times M^{(l+1)}$，也就是说，$M^{(l+1)}$的大小决定了该下一层特征的维度大小。

2.一个实现GCNs传递过程的小栗子

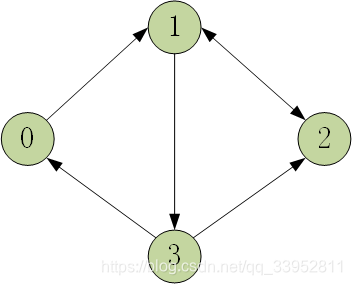
考虑如下图所示的图结构

根据上一小节的介绍，我们现在开始实现一个GCNs传递过程的小栗子，那么，我们现在需要的相关常量和变量有：

1. 图$G=(V,E)$，我们用邻接矩阵$A$来表述$G$，代码利用np.matrix()来实现，同时定义的是其维度为$N\times N$大小，$N=4$个节点。其中，对于邻接矩阵而言，1表示节点$i$到节点$j$可以直达，0表示不可直达。

   import numpy as np
   A = np.matrix([[0, 1, 0, 0],[0, 0, 1, 1], [0, 1, 0, 0],[1, 0, 1, 0]],dtype=float
   )
   

2. 特征矩阵，上一节我们知道，特征矩阵$H$的维度为$N\times M^{(l)}$，这里假定初始化矩阵为$4\times 2$，也就是$M^{(0)}=2$，代码如下：

   H0 = np.matrix([[0,0],[1,1],[2,1],[3,3]],dtype=float
   )#这里的特征值可以进行随机初始化，尽量避免全是0
   

3. 传播规则（非线性函数）$f$，我们设置为$f(H^{(l)},A)=A{H}^{(l-1)}$，也就是一个最一般的恒等函数，那么有：

   H1 = A*H0		#这里的乘积是矩阵乘积，不是点乘（也就是对应位置点的乘积）
   print(H1)
   '''
   [[1. 1.][5. 4.][1. 1.][2. 2.]]
   '''
   

   可以发现，我们定义的这种恒等函数$f=A{H}^{(l-1)}$，实际上就是每个节点周围节点（可达的节点）的特征的和，比如，节点1可达的节点是2和3，对应的特征分别是$(2,1)，(3,3)$，那么下一层节点1的特征就等于了$(5,4)$。

总结下，其实这个栗子很简单，只要有一点点线性代数的知识就能够掌握。

3.局限性以及解决方法

同时，我们还发现这个小栗子的一些问题，也就是GCNs介绍中提到的两个局限性：

1. 没有将节点自身特征进行相加，也就是说，每个节点只考虑周围可达节点的特征，而没有考虑自身节点的特征
2. 邻接矩阵$A$不是标准化的，这样导致的结果是，在不断传播的过程中，特征值会越来越大，也就是“梯度爆炸”的问题。大家可以算一下，对于$H^{(l)}$，在这个栗子中，迭代次数到50次，最终的特征矩阵数值已经到达9次方级别。

对于解决方法，可以考虑下面两个点：

1. 问题1，可以考虑使用$\hat{A}=A+I$来解决，其中$I$表示单位矩阵
2. 问题2，为了让$A$变成标准化的矩阵，也就是需要让每一行（也就是每一个节点）的和为1，我们引入$D^{-1}A$来替换它，其中，$D$是节点度矩阵，是一个对角矩阵。

下面是完整代码

import numpy as npA = np.matrix([[0, 1, 0, 0],[0, 0, 1, 1],[0, 1, 0, 0],[1, 0, 1, 0]],dtype=float
)
H0 = np.matrix([[0, 0],[1, 1],[2, 1],[3, 3]],dtype=float
)D = np.array(np.sum(A, axis=0))[0] #先求出每个节点可达的节点个数
D = np.matrix(np.diag(D))#然后转换为对称矩阵'''改之前'''
New_H = A*H0  #第一层
for i in range(1,100):New_H = A*New_H
print(New_H)'''改之后'''
C = D**-1
New_H = C*A*H0  #第一层
for i in range(1,100):New_H = C*A*New_H
print(New_H)'''
结果：
[[2.20694566e+18 1.74017969e+18][3.35760234e+18 2.64747407e+18][2.20694566e+18 1.74017969e+18][2.90124240e+18 2.28763363e+18]][[1.63636419 1.27272762][1.63636312 1.27272678][0.8181821  0.63636381][2.45454538 1.90909121]]
'''

可以发现，明显解决了梯度爆炸的问题，原理其实也很简单，在每次迭代的时候，每一个节点的每个特征值都乘了一个对应的权重值，权重值的和为1，避免了不断累加导致的梯度爆炸的问题。（感觉有点类似ResNet提出残差块的意味，但是这种方法对于图结构而言则更加的简单且巧妙）

4.回到我们的原始话题

回到原来的话题，我们的目标是构建一个非线性函数的映射关系式，这个关系式（或者说网络模型）能够输入$N\times D$维度的特征矩阵$H$，以及$N\times N$维度的邻接矩阵$A$，输出$N\times F$维度的特征矩阵$Z$。
$$f(H^{(l)},A)=\sigma (A{H}^l{W}^l)$$
基于改进后的方案，我们再重新定义所有的变量：

1. 图$G=(V,E)$，我们用邻接矩阵$A$来表述$G$

   import numpy as np
   A = np.matrix([[0, 1, 0, 0],[0, 0, 1, 1], [0, 1, 0, 0],[1, 0, 1, 0]],dtype=float
   )
   

2. 度矩阵$D$

   D = np.array(np.sum(A, axis=0))[0] 	#先求出每个节点可达的节点个数
   D = np.matrix(np.diag(D))			#然后转换为对称矩阵
   

3. 特征矩阵$H$

   H0 = np.matrix([[0,0],[1,1],[2,1],[3,3]],dtype=float
   )	#这里的特征值可以进行随机初始化，尽量避免全是0
   

4. 权重值$W$，权重值的维度也可以决定下一步维度的变化，在这里维度设置$2\times 2$，维度保持不变

   W = np.matrix([[1, -1],[-1, 1]]
   )
   

5. 传播规则（非线性函数）$f$，设为$f(H^{(l)},A)=\sigma (D^{-1}A{H}^l{W}^l)$，$\sigma$设为$ReLU$函数：

   def func_relu(X:np.matrix):# 负数设为0，正数不变X[X<0] = 0return X
   

这样，我们就定义好了一个传播规则，试一下

import numpy as np
A = np.matrix([[0, 1, 0, 0],[0, 0, 1, 1],[0, 1, 0, 0],[1, 0, 1, 0]],dtype=float
)
H0 = np.matrix([[0, 0],[1, 1],[2, 1],[5, 3]],dtype=float
)
W = np.matrix([[1, -1],[-1, 1]]
)
def func_relu(X:np.matrix):X[X<0] = 0return XD = np.array(np.sum(A, axis=0))[0] #先求出每个节点可达的节点个数
D = np.matrix(np.diag(D))#然后转换为对称矩阵C = D**-1*AH1 = func_relu(C*H0*W)
H2 = func_relu(C*H1*W)
H3 = func_relu(C*H2*W)print(H3)
'''
[[0.5   0.   ][0.375 0.   ][0.25  0.   ][2.25  0.   ]]
'''

5.拿出一个栗子——Zachary的空手道俱乐部

接下来，我们将利用Zachary的空手道俱乐部这个数据集，来具体向大家展示，GCNs的一个实际应用的栗子。

Zachary空手道俱乐部是一个常用的社交网络，节点代表空手道俱乐部的成员，边代表成员之间的相互关系。当Zachary在空手道俱乐部时搞研究时，管理员和教练之间发生了冲突，导致俱乐部一分为二，即两个派别（或者说是类别）。下图是网络的图表示，节点根据俱乐部的哪个部分进行标记。管理员和教练分别被标记为“A”和“I”。

我们的目标是对这些节点，利用欧式空间方式（1维、2维甚至多维的格式）进行表征，以便能够快速区分节点对应的不同派别。

from networkx import to_numpy_matrix,karate_club_graph
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))'''随机初始化参数'''
W_1 = np.random.normal(loc=0.5, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(loc=0.5, size=(W_1.shape[1], 2))'''堆叠GCN层。我们在这里只使用单位矩阵作为特征表征，也就是说，每个节点被表示为一个热门编码的类别变量。'''
def gcn_layer(A_hat, D_hat, X, W):def func_relu(X: np.matrix):X[X < 0] = 0return Xreturn func_relu(D_hat**-1 * A_hat * X * W)
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2'''提取特征表征'''
feature_representations = {node: np.array(output)[node]for node in zkc.nodes()
}def plot_graph(G, weight_name=None):'''G: a networkx Gweight_name: name of the attribute for plotting edge weights (if G is weighted)'''plt.figure()pos = nx.spring_layout(G)edges = G.edges()weights = Noneif weight_name:weights = [int(G[u][v][weight_name]) for u, v in edges]labels = nx.get_edge_attributes(G, weight_name)nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)nx.draw_networkx(G, pos, edges=edges, width=weights);else:nodelist1 = []nodelist2 = []for i in range(34):if zkc.nodes[i]['club'] == 'Mr. Hi':nodelist1.append(i)else:nodelist2.append(i)nx.draw_networkx_nodes(G, pos, nodelist=nodelist1, node_size=300, node_color='r',with_label=True)nx.draw_networkx_nodes(G, pos, nodelist=nodelist2, node_size=300, node_color='b',with_label=True)nx.draw_networkx_edges(G, pos, edgelist=edges, alpha=0.4, with_label=True)plt.show()plot_graph(zkc)for i in range (34):if zkc.nodes[i]['club'] == 'Mr. Hi':plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,color = 'b',s = 100)else:plt.scatter(np.array(output)[i,0],np.array(output)[i,1] ,color = 'r',s = 100)
# plt.scatter(np.array(output)[:,0],np.array(output)[:,1])
plt.show()
'''注意，在这个例子中，随机初始化的权值很可能作为ReLU函数的结果在x轴或y轴上给出0值，因此需要多试几次。'''

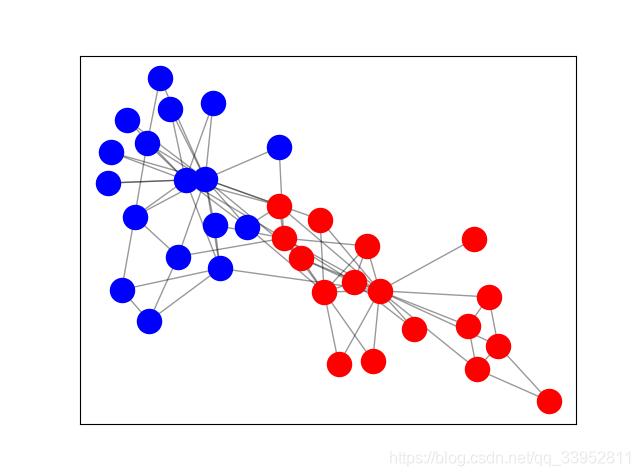
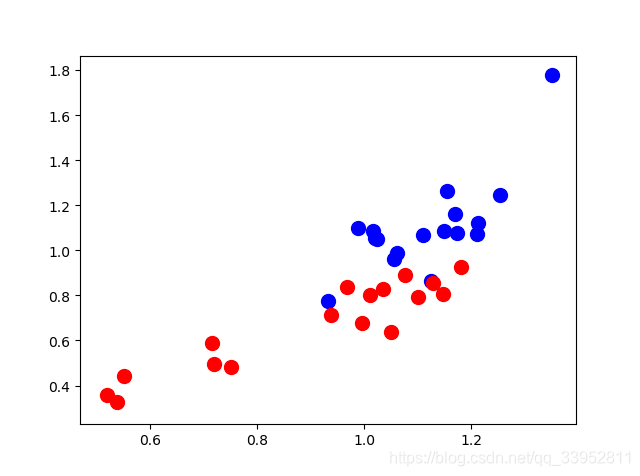
上图是空手道俱乐部的原始图结构表示，红色和蓝色分别代表两个派别。同时，我们的目标是对这些节点，利用欧式空间方式（1维、2维甚至多维的格式）进行表征，以便能够快速区分节点对应的不同派别。同时，下图是还没有经过GCNs模型训练就得到的结果，参考代码，具体而言，最终的输出是$34\times 2$维的数，实际上在笛卡尔坐标系上进行展示就能够能明显的看到，两个派别的具有很强的区分性。

6.总结

在这篇文章中，我们对图卷积网络进行了一个简要介绍，并说明了GCN中每一层节点的特征表征是如何基于其邻域进行聚合的。并通过numpy、networks相关工具包实现了GCNs传递过程的小栗子和一个实例，展示了其强大之处：即使是随机初始化的GCNs，未经过训练，也能Zachary的空手道俱乐部中分离出不同的派别。

参考：

1.https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780

2.networks绘图 https://blog.csdn.net/qq_19446965/article/details/106745837

3.club绘图参考https://blog.csdn.net/qq_36793545/article/details/84844867