1、电路综合原理与实践---电抗函数的综合原理

本文主要是介绍1、电路综合原理与实践---电抗函数的综合原理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、电路综合原理与实践—电抗函数的综合原理

进行电路设计的时候，总是有人会问，哎你这个匹配电路怎么设计的，基于什么原理啊。我总回答的支支吾吾没有底气，实际我想说，我什么理论都没有，弄个几段微带线然后用ADS优化一下就出来了。不知道大家是不是也这样，毕竟我不是专门研究电路理论的嘛，不会也很正常是不是噻。

开个玩笑，在之前我们简要介绍了匹配电路的设计方法，主要包括：
1、基于Smith圆图进行匹配：06、ADS使用记录之分布式参数匹配
2、使用低通滤波匹配电路：25、基于原型的切比雪夫低通滤波器匹配设计理论
26、ADS使用记录之基于低通滤波匹配的超宽带功率放大器设计
其中的微带线等效原理在下面这个教程中介绍过：24、基于原型的切比雪夫低通滤波器设计理论（插入损耗法）（给出了matlab代码，计算集总参数的等效微带线电路非常方便）

其实很多里面都用到了上面两个方法，如果想进一步学习可以参考博主其他的教程哦。

在此介绍第三种电路设计方法，就是网络综合法。可能有人对此听说不多，实际上是很古老的原理了，但是实际上现在很多论文的电路设计都是基于此方法。其实际上是基于策动点阻抗（导纳）函数进行网络综合，而策动点阻抗（导纳）函数如何得来呢，那就是使用简化实频技术（SRFT）。简化实频技术之后会介绍，在此先介绍基于策动点阻抗（导纳）函数进行网络综合的方法。

1、基于Smith圆图进行匹配与使用低通滤波匹配电路的劣势

基于Smith圆图进行匹配劣势非常大，它不是一个专门用于宽带电路设计的方法，做窄带的适合匹配一下还行。而且就算能使用低Q值进行匹配，除中心频率处的阻抗实际上我们是无法控制的，还需要进一步进行调谐。

基于低通滤波匹配技术进行匹配实际上适用于宽带的设计，然而其依然有两个劣势，那就是将实数阻抗匹配到复数阻抗效果可能不理想，还需要进一步进行调谐。可以参考这篇文章里面的效果：25、基于原型的切比雪夫低通滤波器匹配设计理论。其次这种技术严格意义上没办法控制谐波，因此可能还需要额外的设计或者调谐，当时这是对于PA的设计来说的。

但是基于简化实频技术（SRFT）的网络综合法可以避免这些问题，指哪儿打哪儿。

此处推荐学习网络综合法的教科书，那就是吴宁老师的电网络分析与综合吴宁老师的电网络分析与综合PDF。在此推荐简化实频技术（SRFT）的教科书，那就是Pierre Jarry; Jacques N. Beneat的Microwave_Amplifier_and_Active_Circuit_Design_Using_the_Real_Frequency_Technique，这本书没有中文版本使用简化实频进行电路设计的教科书。下面开始对网络综合理论进行介绍。

2、电抗函数的实现原理

此处参考吴宁老师的电网络分析与综合吴宁老师的电网络分析与综合PDF。严格意义上来讲，一个网络实现怎么样匹配效果，可以完全由策动点阻抗函数来决定。在此介绍通过策动点阻抗来进行网络综合的方法。

1、福斯特实现
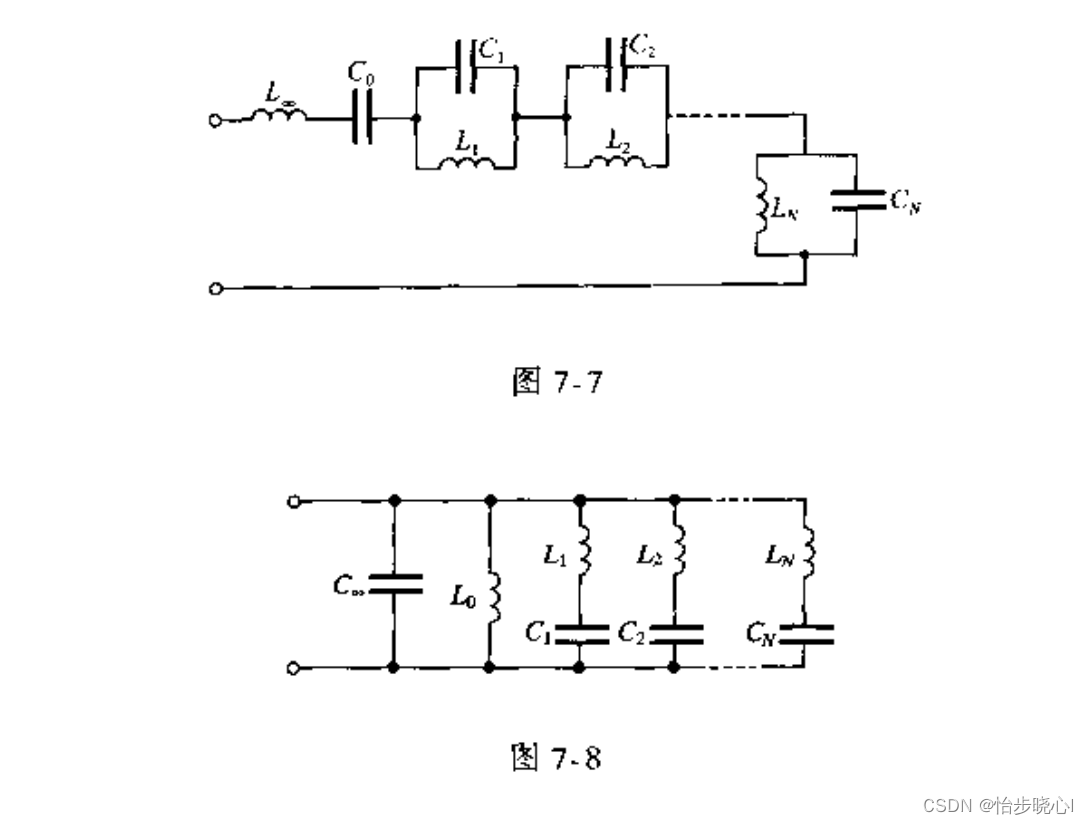
福斯特实现分为Ⅰ型和Ⅱ型，本质上是一样的。其基本结构是电容和电感串并联，典型电路如下所示，第一个是福斯特Ⅰ型，第二个是福斯特Ⅱ型。
在这里插入图片描述
2、考尔实现
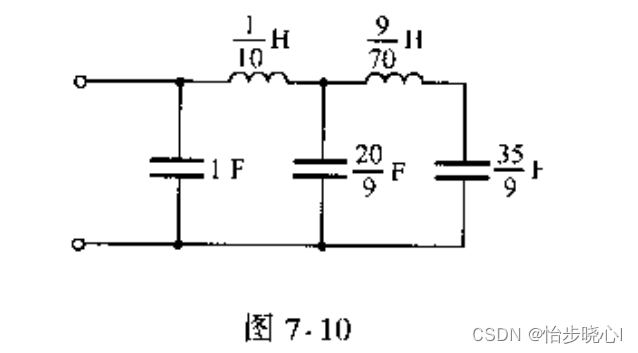
考尔实现分为Ⅰ型和Ⅱ型，本质上是一样的。其基本结构是电容和电感串并交替，典型电路如下所示。其中上面那个是考尔Ⅰ型，其特征为并联电容器。下面那个是考尔Ⅱ型，其特征为并联电感器。
在这里插入图片描述

3、电抗函数的Matlab综合

此处以吴宁老师的电网络分析与综合PDF书中的例7-6为例，其原题为：
在这里插入图片描述

在此使用Matlab编程进行电路的直接求解，求解的部分代码如下，代码会在最后给出全部工程：

clear 
clcsyms s;Zsym = (s^4 + 10*s^2 +9)/(s^3 + 2*s);
pretty(Zsym)[Zn, Zd] = sym2nd(Zsym);% Note: THe inputs to NetSynth are flipped and it is marked as being in
% admittance mode
synth = NetSynth(Zd, Zn);
synth.is_admit = true;synth.generate('Cauer1');
% synth.generate('Cauer2');
% synth.generate('Foster1');
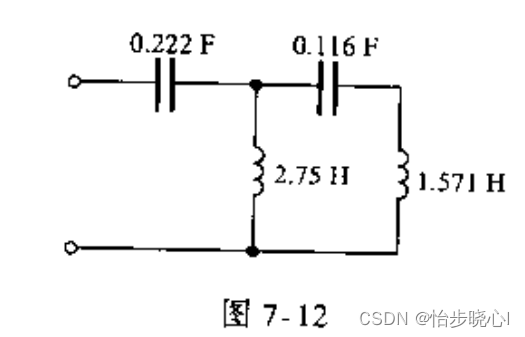
% synth.generate('Foster2');disp(synth.circ.str());

考尔Ⅰ型
上述代码进行的是考尔Ⅰ型的综合代码，求解得到的网络拓扑结果如下：

+------+-----------+--------+--------+-----+-----------+
| Ref. |   Value   | Node 1 | Node 2 |  Z0 | Stub Type |
+------+-----------+--------+--------+-----+-----------+
|    L1|         1H|      IN|      n1|  N/A|        N/A|
|    C1|     0.125F|      n1|     GND|  N/A|        N/A|
|    L2|    9.1429H|      n1|      n2|  N/A|        N/A|
|    C2|  0.097222F|      n2|      n3|  N/A|        N/A|
+------+-----------+--------+--------+-----+-----------+

由此得到的综合出的考尔Ⅰ的电路图如下所示：
在这里插入图片描述
考尔Ⅱ型
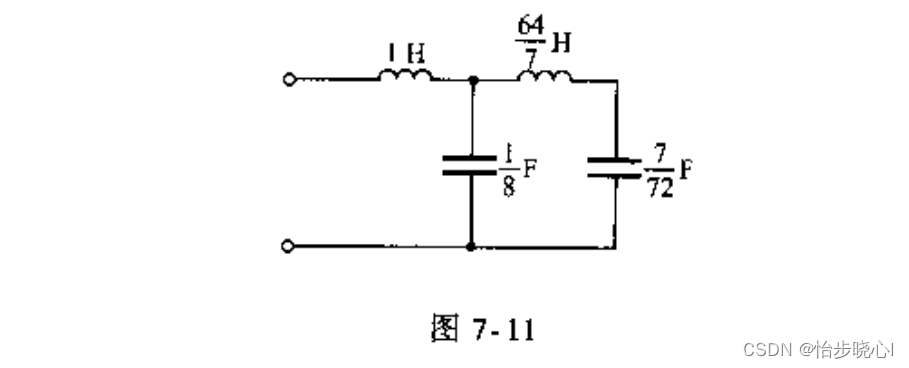
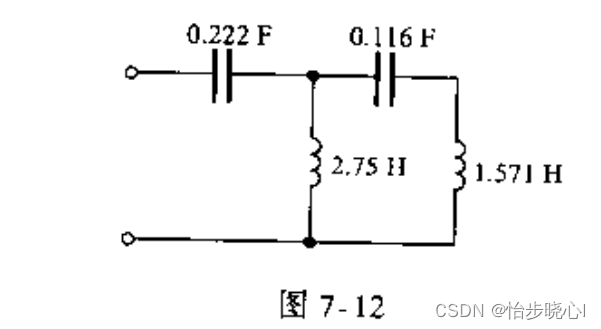
修改一下上面的注释，使用考尔Ⅱ型进行综合得到的电路拓扑参数如下所示：

+------+----------+--------+--------+-----+-----------+
| Ref. |   Value  | Node 1 | Node 2 |  Z0 | Stub Type |
+------+----------+--------+--------+-----+-----------+
|    C1|  0.22222F|      IN|      n1|  N/A|        N/A|
|    L1|     2.75H|      n1|     GND|  N/A|        N/A|
|    C2|   0.1157F|      n1|      n2|  N/A|        N/A|
|    L2|   1.5714H|      n2|      n3|  N/A|        N/A|
+------+----------+--------+--------+-----+-----------+