本文主要是介绍tamarin-manual(一到五)20230926271007,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
简介
Tamarin power 是一种功能强大的工具,用于对安全协议进行符号建模和分析。它以安全协议模型为输入,指定了以不同角色(如协议启动者、响应者和受信任的密钥服务器)运行协议的代理所采取的行动,敌手的指定以及协议期望属性的指定。然后,Tamarin 可用于自动构建一个证明,即即使协议角色的任意多个实例并行交错,加上敌手的行动,协议也能满足其指定的属性。在本手册中,我们将概述这一工具及其使用方法。
Tamarin 为安全协议建模和推理提供一般支持。使用基于多集重写规则(multiset rewriting rules)的表达式语言(expressive language)来指定协议和敌手。这些规则定义了一个带标记的转换系统,其状态由敌手知识的符号表示、网络信息、新生成值信息和协议状态组成。敌手和协议通过更新网络信息和生成新信息进行交互。Tamarin 还支持某些加密运算符的等式规范,如 Diffie-Hellman 指数化和双线性配对。安全属性被建模为轨迹属性,根据转换系统的轨迹或两个转换系统的观测等价性进行检查。
Tamarin 提供两种构建证明的方法。它有一个高效的全自动模式,将演绎和等式推理与启发式方法相结合,以指导证明搜索。如果该工具的自动证明搜索结束,它将返回正确性证明(针对数量不限的角色实例和新值)或反例,反例代表违反所述属性的攻击。不过,由于安全协议的正确性是一个无法判定的问题,因此该工具可能无法在给定的验证问题上终止。因此,用户可能需要借助 Tamarin 的交互模式来探索证明状态、检查攻击图,并将手动证明指导与自动证明搜索无缝结合起来。
(Schmidt 2012) 和 (Meier 2012) 的论文对Tamarin的基础进行了正式论述。我们在此仅作简要(技术)总结。对于定义加密算子的等式理论 E、定义协议的多集重写系统 R 和定义迹属性的公式ϕ,Tamarin 可以检查 R modulo E 的迹的有效性或可满足性。通常,有效性检查简化为检查否定式的可满足性。在这里,约束求解用于对具有满足迹线的执行进行穷举式符号搜索。搜索的状态是约束系统。例如,一个约束可以表示在执行中出现了某个多集重写步骤,或者一个步骤出现在另一个步骤之前。我们还可以直接使用公式作为约束,来表达某些行为不会在执行中出现。限制缩减规则的应用,如简化或情况区分,相当于增量构建满足要求的轨迹。如果无法应用更多规则,也找不到令人满意的轨迹,那么就不存在令人满意的轨迹。对于符号推理,我们利用有限变体特性(Comon-Lundh 和 Delaune,2005 年)将相对于 R 的 E 模推理简化为相对于 R 变体的 AC 模推理。
本手册是为希望使用 Tamarin 对安全协议进行建模和分析的研究人员和从业人员编写的。我们假定读者熟悉基本密码学和安全协议的基本工作原理。我们的重点是解释 Tamarin 的用法,以便新用户能够下载、安装和使用该系统。我们并不试图描述 Tamarin 的形式基础,读者可参阅相关论文和科学论文了解这些细节。
实践证明,Tamarin 工具非常成功。它支持跟踪和观察等价性、自动和交互模式,并内置了对等价理论的支持,如模拟 Diffie-Hellman 密钥交换的等价理论。它支持(有限的)归纳形式,并能高效地并行搜索证明。它已被应用于不同领域的众多协议,包括:
基于 Diffie-Hellman 指数的高级密钥协议,如根据 eCK(扩展的 Canetti Krawczyk)模型验证 Naxos;见(Schmidt 等人,2012 年)。
抗攻击公钥基础设施(ARPKI)(Basin 等人,2014 年)。
传输层安全(TLS)(Cremers 等人,2016 年)
及其他
在下一节 "安装 "中,我们将介绍如何安装 Tamarin。然后,我们建议初次使用 Tamarin的用户阅读 "第一个示例 "部分,该部分详细描述了一个简单的协议分析,但不涉及技术细节。接下来,我们将系统地介绍用户所需的技术背景,首先在 "加密信息 "一节中介绍加密信息,然后在第 5 节和第 6 节中介绍两种不同的建模方法,包括使用规则的协议规范和使用流程的协议规范。然后在 "属性规范 "一节中介绍属性规范。
然后,我们将在 "预计算 "一节中继续介绍预计算,并在 "建模问题 "一节中介绍可能的建模问题。之后,我们将在 "高级功能 "一节中为有经验的用户介绍高级功能。我们在 "案例研究 "一节中列出了已完成的案例研究。工具链部分介绍了其他输入工具链。在 "局限性 "一节中介绍了局限性。本手册的最后,我们在 "联系信息和进一步阅读 "中提供了联系信息和进一步阅读。
安装
在 macOS 或 Linux 上安装
在 macOS 或 Linux 上安装 Tamarin 的最简单方法是使用 Homebrew:
brew install tamarin-prover/tap/tamarin-prover
它单独打包用于
- Arch Linux: pacman -S tamarin-prover
- Nixpkgs: nix-env -i tamarin-prover
- NixOS:将 tamarin-prover 添加到你的environment.systemPackages 中。
您也可以直接从 GitHub 下载二进制文件,然后自己手动安装依赖项,或从源代码编译。
在 Windows 10 上安装
(在Ubuntu上安装总出现各种错误,就放弃了,最后在Windows上成功安装)
您可以使用 Windows Subsystem for Linux(WSL)在 Windows 10 下安装 Tamarin(带图形用户界面)。出于性能和兼容性考虑,我们建议使用 WSL2 和 Ubuntu。安装好 WSL 和 Ubuntu 后,启动 Ubuntu 应用程序,按照上述 Linux 安装说明安装 Tamarin。然后就可以在 Ubuntu 应用程序中使用常规命令运行 Tamarin。要使用交互式模式,请在应用程序内启动 Tamarin,并将常用的 Windows 浏览器连接到 http://127.0.0.1:3001。在 Ubuntu 应用程序中,您可以通过 /mnt/c 访问 Windows 文件,例如 C: 驱动器上的文件。
从源代码编译
除非你正在为 Tamarin 开发新功能,或者你想使用未发布的功能,否则你不需要从源代码编译 Tamarin。不过,如果你确实想从源代码中安装它,你可以使用以下方法:
手动安装依赖项
Tamarin 需要 Haskell Stack 才能构建,GraphViz 和 Maude(2.7.1 或更新版本)才能运行。最简单的安装方法是
brew install tamarin-prover/tap/maude graphviz haskell-stack
或者,您也可以自己安装:
- Haskell Stack 按照 Stack 安装页面给出的说明进行安装。如果使用软件包管理器安装堆栈(尤其是在 Ubuntu上),则必须在安装后运行堆栈升级,因为该版本的堆栈通常已经过时。
- Graphviz Graphviz 应可使用标准软件包管理器或直接从 http://www.graphviz.org/ 获取。
- 您可以使用软件包管理器安装 Maude(确保版本为 2.7.1 或更新)。你也可以从 [Maude 网站] (http://maude.cs.illinois.edu/w/index.php/Maude_download_and_installation) 手动安装 Maude。在这种情况下,应确保 PATH 包括安装路径,以便调用 maude 运行正确的版本。请注意,尽管 Maude 可执行文件是可移动的,但 prelude.maude 文件必须位于启动 Maude 的同一文件夹中。
编译
查看源代码
git clone https://github.com/tamarin-prover/tamarin-prover.git
就可以编译当前的开发版本了。如果您想使用主版本,只需运行 git checkout master 即可。
无论哪种情况,你都可以在新目录中运行 make default,它将为你的系统安装合适的 GHC( Glasgow Haskell 编译器),包括所有依赖项。tamarin-prover 可执行文件将被复制到 ~/.local/bin/tamarin-prover。请注意,这个过程将耗时 30 到 60 分钟,因为所有依赖项(大约 120 个)都要从头开始编译。如果你后来拉取了更新版本的 Tamarin(或从主分支切换到/从主分支),那么只需重新编译工具本身,这最多需要几分钟时间。
在远程机器上运行 Tamarin
如果您可以使用速度更快的台式机或服务器,但更喜欢在笔记本电脑上使用 Tamarin,您也可以这样做。这样,该工具的CPU/内存密集型推理部分就会在速度更快的机器上运行,而您只需在本地运行图形用户界面,即您选择的网络浏览器。为此,您可以使用以下命令将您的端口 3001 转发到服务器的端口 3001,并适当替换 SERVERNAME。
ssh -L 3001:localhost:3001 SERVERNAME
如果您这样做,我们建议您在屏幕环境中运行服务器上的 Tamarin 实例,即使网络连接中断,该实例也会继续运行,因为您可以稍后重新连接到网络。否则,任何网络故障都可能要求你重启 Tamarin 并重新开始验证。
Tamarin 代码编辑器
在 Tamarin Prover 项目中包含的 etc 文件夹下,有适用于 VIM、Sublime Text 3、Emacs 和 Notepad++ 的插件。下面我们将详细介绍安装首选插件所需的步骤。
VIM
使用 Vim 插件管理器
本示例将使用 Vundle 直接从该版本库安装插件。以下说明应可翻译成其他插件管理器。
- 确保你安装了 Vundle(或你喜欢的插件管理器)
- 在 .vimrc 中输入以下内容或类似说明:
Plugin 'tamarin-prover/editors'
- 重启 Vim 或重新加载配置
- 运行 Vim 命令 :
PluginInstall(或类似命令)
您可以通过:PluginUpdate安装更新。
手动安装(不推荐)
如果使用此方法安装 Vim 支持文件,则需要自行更新文件。
- 创建
~/.vim/目录(如果尚未存在),这是$VIMRUNTIME的典型位置 - 将
etc/vim的内容复制到~/.vim/,包括文件夹。
Sublime Text 3
editor-sublime 是为 Sublime Text 3 编辑器开发的一个插件。该插件具有以下功能: - 基本语法 - 理论、规则、限制和定理片段
editor-sublime 有两种安装方式:
第一种也是首选的方法是使用 PackageControl.io。现在可以通过 sublime 软件包管理器安装 editor-sublime。请参阅安装和使用文档,然后搜索并安装 TamarinProver。
或者也可以从源代码安装。对于 Linux / macOS,也可按照此流程安装。我们假设您已安装了 git 工具。
- 将目录更改为 Sublime Text 软件包目录:
macOS:cd ~/Library/Application\Support/Sublime\ Text\ 3/Packages/
Linux:cd ~/.config/sublime-text-3/Packages/ - 将该目录克隆到 Packages 文件夹中。
SSH:git clone git@github.com:tamarin-prover/editor-sublime.git
HTTPS:git clone https://github.com/tamarin-prover/editor-sublime.git - 关闭并重新打开 Sublime,在右下角的语法列表中,"Tamarin "应出现在列表中。
请注意,该插件正在积极开发中,因此其中一些功能仍以原型方式实现。如果您在运行插件的任何部分时遇到任何问题或有任何疑问,请访问该项目的 GitHub 页面。
Notepad++
使用 notepad_plus_plus_spthy.xml 文件,按照 Notepad++ Wiki中的步骤操作。
Emacs
spthy.el 实现了 SPTHY 主模式。你可以用 M-x load-file 加载它,或者用你喜欢的方式将它添加到你的 .emacs 中。
Atom
language-tamarin 软件包为 Atom 提供 Tamarin 语法高亮。要安装它,请运行 apm install language-tamarin
FAQ
如何使用Homebrew卸载 Tamarin?
要卸载(并 "取消 " Tamarin homebrew tap),请执行以下操作
- brew uninstall tamarin-prover- brew untap tamarin-prover/tap
这个homebrew-science tap是怎么回事?
Tamarin 以前是在现已关闭的homebrew-science tap(homebrew-science tap)中发布的。如果你已经通过 Homebrew 安装了它,可能需要先卸载并取消该版本:
brew uninstall tamarin-prover
brew untap homebrew/science
更新/拉动/释放后,Tamarin 不再编译。
请尝试运行堆栈升级和堆栈更新。过期的堆栈版本会导致编译错误。
第一个例子
初始示例
我们将从一个简单的协议例子开始,该协议只包含两条信息,这里用所谓的 Alice-and-Bob 符号来表示:
C -> S: aenc(k, pkS)
C <- S: h(k)
在这个协议中,客户端 C 生成一个新的对称密钥 k,用服务器 S 的公钥 pkS 加密(aenc 表示非对称加密),然后发送给 S。
这个简单的协议是人为的,只能满足很弱的安全保证。我们将用它来说明一般的 Tamarin 工作流程,证明从客户端的角度来看,只要服务器不被入侵,新生成的密钥就是秘密的。默认情况下,对手是一个控制网络的 Dolev-Yao 对手,可以删除、注入、修改和拦截网络上的信息。
协议的 Tamarin 模型及其安全属性在文件 FirstExample.spthy 中给出(.spthy 代表安全协议理论),可在本教程的 github 仓库(https://github.com/tamarin-prover/manual)中的代码文件夹中找到。Tamarin 文件以 theory 开头,后跟理论名称,此处为 FirstExample。
theory FirstExample
begin
在关键字 begin 之后,我们首先声明协议使用的加密基元。之后,我们声明了协议模型的多集重写规则,最后我们写下了需要证明的属性(在 Tamarin 框架中称为lemmas),这些属性指定了协议所需的安全属性。请注意,我们还插入了注释以构建理论结构。
接下来,我们将详细解释协议模型。
密码基元
我们采用的是安全协议的符号模型。这意味着我们将信息建模为术语,由满足描述其属性的基础等式理论的函数构建而成。这将在密码信息部分详细解释。
在本例中,我们使用 Tamarin 内置的散列和非对称加密函数,声明如下:
builtins: hashing, asymmetric-encryption
这些内置函数为我们提供了
- 表示加密散列函数的一元函数
h - 二进制函数
aenc,表示非对称加密算法 - 表示非对称解密算法的二进制函数
adec - 表示与私钥相对应的公钥的一元函数
pk
此外,内置密钥还规定,使用正确的私人密钥对密文进行解密后,将返回初始明文,即 adec(aenc(m, pk(sk)), sk) 被还原为m。
公钥基础设施建模
在 Tamarin 中,协议及其环境使用多集重写规则建模。这些规则对系统的状态进行操作,而系统的状态是以事实的多集(即一个包)来表示的。事实可以看作是存储状态信息的谓词。例如,事实 Out(h(k)) 表示协议在公共频道上发送了信息 h(k),事实 In(x) 表示协议在公共频道上接收了信息 x。
本例从公钥基础设施(PKI)模型开始。同样,我们使用事实来存储其参数所给出的状态信息。规则有前提和结论,以箭头符号-->分隔。执行规则要求前提中的所有事实都存在于当前状态中,执行的结果是,结论中的事实将被添加到状态中,而前提则被移除。现在我们来看看第一条规则,它模拟了公钥的注册:
rule Register_pk:[ Fr(~ltk) ]-->[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]
这里唯一的前提是 Fr 事实的实例。Fr 事实是一个内置事实,表示一个新生成的名称。这种机制用于模拟随机数,如 nonces 或密钥(详见《模型规范》)。
在 Tamarin 中,变量的排序用前缀表示:
- ~x 表示 x:fresh
- $x 表示 x:pub
- %x 表示 x:nat
- #i 表示 i:temporal
- m 表示 m:msg
此外,字符串常量 "c "表示 pub 中的公共名称,这是一个固定的全局常量。我们有一个最高排序 msg 和该最高排序的三个不可比子排序 fresh、pub 和 nat。排序 temporal 的时间点变量是不相连的。
因此,上述规则可以解读如下。首先,生成一个新名称 ~ltk(排序为 fresh),即新的私钥,并为我们要生成密钥对的代理非确定地选择一个公钥名称 A。然后,生成事实 !Ltk($A,~ltk)(感叹号 ! 表示事实是持久的,即可以任意频繁地使用),表示代理 A 与其私钥 ~ltk 之间的关联,并生成事实 !Pk($A,pk(~ltk)),表示代理 A 与其公钥 pk(~ltk) 之间的关联。
在本例中,我们允许对手使用以下规则检索任何公钥。本质上,它读取一个公钥数据库条目,并使用内置事实 Out 将公钥发送到网络,Out 表示向网络发送信息(更多信息请参阅 "模型规范 "部分)。
rule Get_pk:[ !Pk(A, pubkey) ]-->[ Out(pubkey) ]
我们用以下规则来模拟长期私钥的动态泄露。直观地说,它读取一个私钥数据库条目并将其发送给对手。这条规则有一个可观测的 LtkReveal 行动,说明代理 A 的长期密钥已被泄露。行动事实就像事实一样,但与其他事实不同的是,它不出现在状态中,而只出现在轨迹上。安全属性是在轨迹上指定的,下面将使用 LtkReveal 动作来确定哪些代理被入侵。该规则现在有前提、结论和箭头内的行动事实:--[ ACTIONFACT ]->:
rule Reveal_ltk:[ !Ltk(A, ltk) ]--[ LtkReveal(A) ]->[ Out(ltk) ]
协议建模
回顾一下我们要模拟的协议的爱丽丝和鲍勃符号:
C -> S: aenc(k, pkS)
C <- S: h(k)
我们用以下三条规则来模拟它。
// Start a new thread executing the client role, choosing the server
// non-deterministically.启动一个新线程,执行客户端角色,非确定地选择服务器 非确定地选择服务器。
rule Client_1:[ Fr(~k) // choose fresh key选择新鲜的密钥, !Pk($S, pkS) // lookup public-key of server查找服务器的公钥]-->[ Client_1( $S, ~k ) // Store server and key for next step of thread为下一步线程存储服务器和密钥, Out( aenc(~k, pkS) ) // Send the encrypted session key to the server向服务器发送加密会话密钥]rule Client_2:[ Client_1(S, k) // Retrieve server and session key from previous step从上一步读取服务器和会话密钥, In( h(k) ) // Receive hashed session key from network从网络接收散列会话密钥]--[ SessKeyC( S, k ) ]-> // State that the session key 'k'[] // was setup with server 'S'说明会话密钥 "k "是与服务器 "S "设置的// A server thread answering in one-step to a session-key setup request from
// some client.服务器线程一步到位地响应某个客户端的会话密钥设置请求
rule Serv_1:[ !Ltk($S, ~ltkS) // lookup the private-key查找私钥, In( request ) // receive a request收到请求]--[ AnswerRequest($S, adec(request, ~ltkS)) ]-> // Explanation below说明如下[ Out( h(adec(request, ~ltkS)) ) ] // Return the hash of the// decrypted request.返回已解密请求的哈希值
在这里,第一条规则模拟客户端发送信息,第二条规则模拟客户端接收响应。第三条规则是服务器的模型,在一条规则中既接收信息又作出回应。
这里有几种解释。首先,Tamarin 使用 C 风格注释,因此 /* 和 */ 之间的所有内容或 // 后面的行都是注释。其次,我们使用一个动作记录服务器收到的会话密钥设置请求,以便稍后为客户端正式确定身份验证属性。
安全性能建模
安全属性是根据协议执行过程中的行为事实轨迹定义的。
我们有两个属性需要评估。在 Tamarin 框架中,要评估的属性用lemmas 表示。第一个是关于从客户端角度看会话密钥的保密性。Lemma Client_session_key_secrecy(客户会话密钥保密)说的是,除非对手对服务器 S 进行了长期密钥揭示,否则不可能出现客户与服务器 S 设置了会话密钥 k 而对手得知了 k 的情况。这就是,对于客户与服务器 S 设置的所有会话密钥 k,必须有一个服务器回应了请求,或者对手先前在 S 上执行了长期密钥揭示。
lemma Client_session_key_secrecy:" /* It cannot be that a 这不可能是一个 */not(Ex S k #i #j./* client has set up a session key 'k' with a server'S' 客户机与服务器'S'设置了会话密钥'k'。*/SessKeyC(S, k) @ #i/* and the adversary knows 'k' 而对手知道'k'*/& K(k) @ #j/* without having performed a long-term key reveal on 'S'. 而没有对 "S "进行长期按键揭示。*/& not(Ex #r. LtkReveal(S) @ r))"lemma Client_auth:" /* For all session keys 'k' setup by clients with a server 'S' 对于客户与服务器 "S "设置的所有会话密钥 "k*/( All S k #i. SessKeyC(S, k) @ #i==>/* there is a server that answered the request有一个服务器响应了请求 */( (Ex #a. AnswerRequest(S, k) @ a)/* or the adversary performed a long-term key reveal on 'S'before the key was setup. 或对手在密钥设置之前对'S'进行了长期密钥揭示*/| (Ex #r. LtkReveal(S) @ r & r < i)))"
请注意,我们还可以将认证属性强化为注入式认证。我们的表述比注入式验证的标准表述更强,因为它是基于唯一性而不是计数。对于大多数保证注入式验证的协议,我们也可以证明这种唯一性声明,因为它们在适当的新鲜数据上达成了一致。这一点在 Lemma Client_auth_injective 中有所说明。
lemma Client_auth_injective:" /* For all session keys 'k' setup by clients with a server 'S' 对于客户与服务器 "S "设置的所有会话密钥 "k*/( All S k #i. SessKeyC(S, k) @ #i==>/* there is a server that answered the request */( (Ex #a. AnswerRequest(S, k) @ a/* and there is no other client that had the same request */& (All #j. SessKeyC(S, k) @ #j ==> #i = #j))/* or the adversary performed a long-term key reveal on 'S'before the key was setup. */| (Ex #r. LtkReveal(S) @ r & r < i)))"
为了确保我们的 Lemmas 不会因为模型不可执行而空洞地成立,我们还包含了一个可执行性 Lemma,表明模型可以运行完成。正如下面的 Lemma Client_session_key_honest_setup(客户_会话_密钥_诚实_设置)所示,该 Lemma 是以普通 Lemma 的形式给出的,但使用了 exists-trace 关键字。这个关键字表示,如果存在公式成立的轨迹,则该 Lemma 为真;这与前面的 Lemmas 不同,前面的 Lemmas 要求公式在所有轨迹上都成立。在对协议建模时,这种存在性证明是有用的正确性检查。
lemma Client_session_key_honest_setup:exists-trace" Ex S k #i.SessKeyC(S, k) @ #i& not(Ex #r. LtkReveal(S) @ r)"
图形用户界面
现在如何证明您的推导是正确的?如果执行命令行
tamarin-prover interactive FirstExample.spthy
然后你将在命令行中看到以下输出:
GraphViz tool: 'dot'checking version: dot - graphviz version 2.39.20150613.2112 (20150613.2112). OK.
maude tool: 'maude'checking version: 2.7. OK.checking installation: OK.The server is starting up on port 3001.
Browse to http://127.0.0.1:3001 once the server is ready.Loading the security protocol theories './*.spthy' ...
Finished loading theories ... server ready at http://127.0.0.1:300121/Jun/2016:09:16:01 +0200 [Info#yesod-core] Application launched @(yesod_83PxojfItaB8w9Rj9nFdZm:Yesod.Core.Dispatch ./Yesod/Core/Dispatch.hs:157:11)
此时,如果出现任何语法或格式错误(例如,如果同一事实被用于不同的 arities,则会显示错误),这些错误也会被显示出来。有关如何处理此类错误的详细信息,请参见 "建模问题 "部分。
不过,在我们的示例中不存在此类错误,因此上述命令将启动一个网络服务器,加载与 FirstExample.spthy 位于同一目录下的所有安全协议理论。将浏览器指向
http://localhost:3001
您将看到以下欢迎界面:
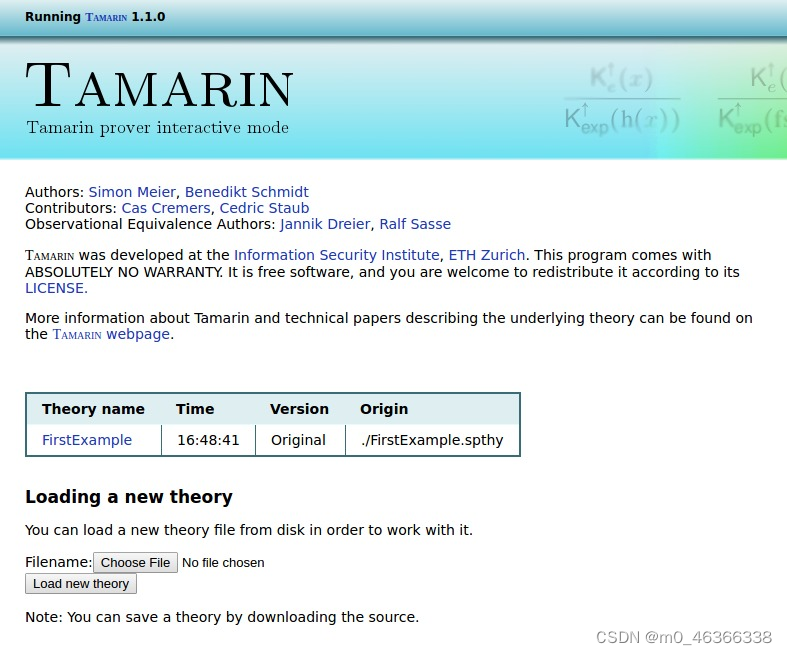
中间的表格显示了所有已加载的理论。你可以点击某个理论进行探索并证明你的安全属性,也可以使用底部的上传表单上传更多理论。请注意,如果以这种方式使用图形用户界面载入更多理论,将不会显示任何警告,因此我们建议从相应目录下的命令行启动 Tamarin。
如果你点击已加载理论表中的 "FirstExample "条目,应该会看到如下内容:
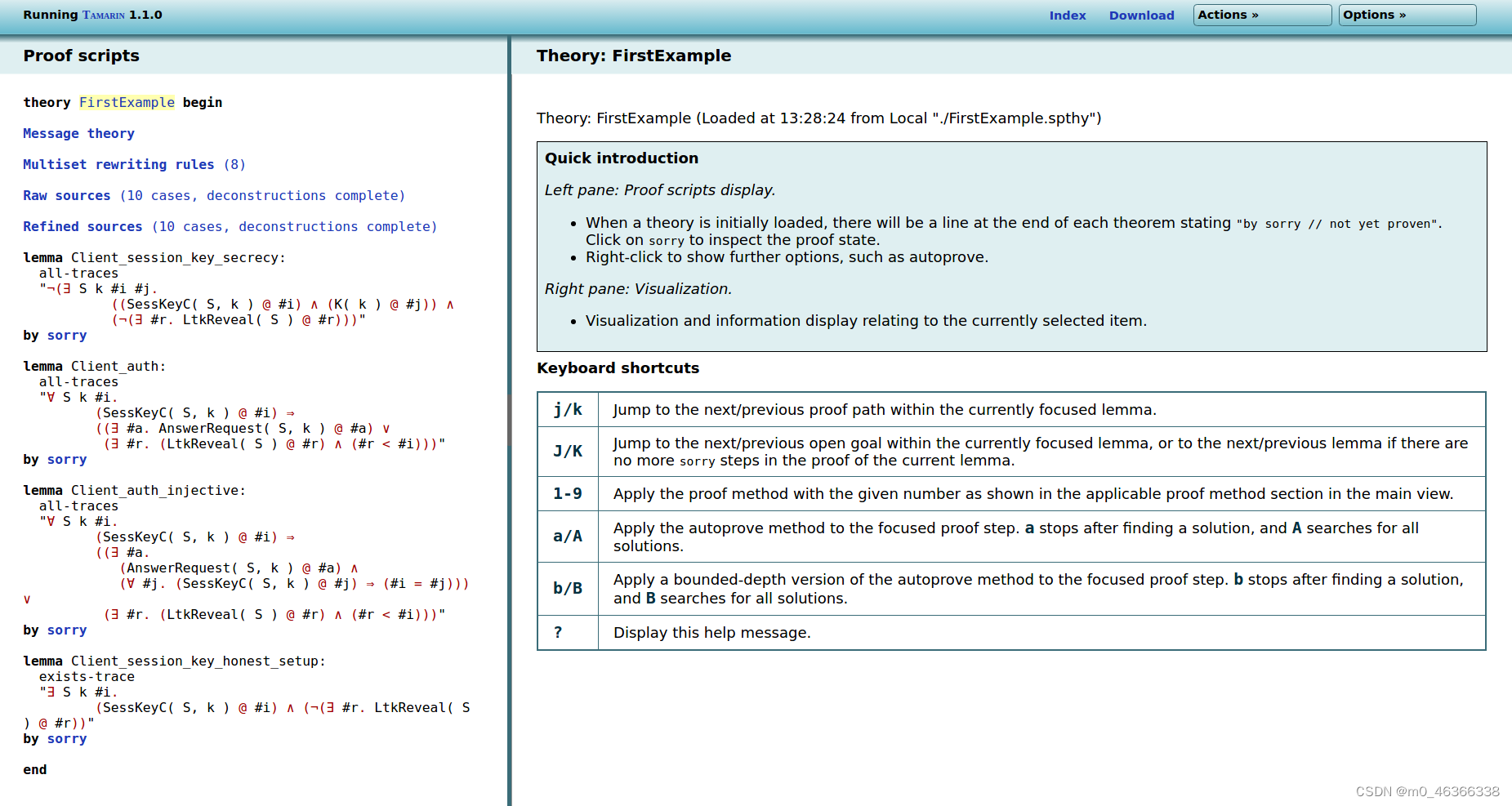
左侧是理论:与描述对手的信息理论、描述协议的多集重写规则和限制、原始和精炼来源的链接,后面是要证明的公理。我们将在下文中逐一解释。
右侧是可用命令和键盘快捷键的快速摘要,您可以使用它们在理论中进行导航。右上角有一些链接: 索引(Index)可以返回欢迎页面;下载(Download)允许您下载当前理论(包括部分证明,如果存在的话);操作(Actions)和显示源代码(Show source)子按钮可以显示理论的源代码;选项(Options)允许您配置图形可视化的详细程度(示例见下文)。
如果点击左侧的 "信息 "理论,您会看到以下内容:

在右侧,您现在可以看到信息理论,首先是所谓的签名,它由所有函数和方程组成。这些函数既可以是用户自定义的,也可以是使用内置函数导入的,就像我们的例子一样。请注意,Tamarin 会自动添加一个函数对来创建线对,并添加函数 fst 和 snd 以及两个方程来访问线对的第一部分和第二部分。有一种使用 < 和 > 来表示函数对的简写方法,例如这里使用的 fst(<x.1,x.2>)。
下面是构造规则。这些规则描述了对手可以应用的函数。例如,请看下面的规则:
rule (modulo AC) ch:[ !KU( x ) ] --[ !KU( h(x) ) ]-> [ !KU( h(x) ) ]
直观地说,这条规则表示如果对手知道 x(由前提中的事实 !KU(x)表示),那么他就可以计算 h(x)(由结论中的事实 !KU(h(x))表示),即 x 的哈希值。
最后是解构规则。这些规则描述了对手可以通过应用函数从更大的术语中提取哪些术语。举例来说,可以考虑以下规则:
rule (modulo AC) dfst:[ !KD( <x.1, x.2> ) ] --> [ !KD( x.1 ) ]
简而言之,这条规则是说,如果对手知道一对 <x.1,x.2>(用事实 !KD( <x.1, x.2> ) 表示),那么他就可以从中提取第一个值 x.1(用事实 !KD( x.1 ) 表示)。这是将 fst 应用于数据对,然后使用方程 fst(<x.1, x.2>) = x.1 的结果。!KD( ) 和 !KU( ) 之间的确切区别目前并不重要,下文将对此进行解释。作为第一近似值,两者都代表了对手的知识,区别只是为了让工具的推理更有效率。
现在点击左侧的多集重写规则。
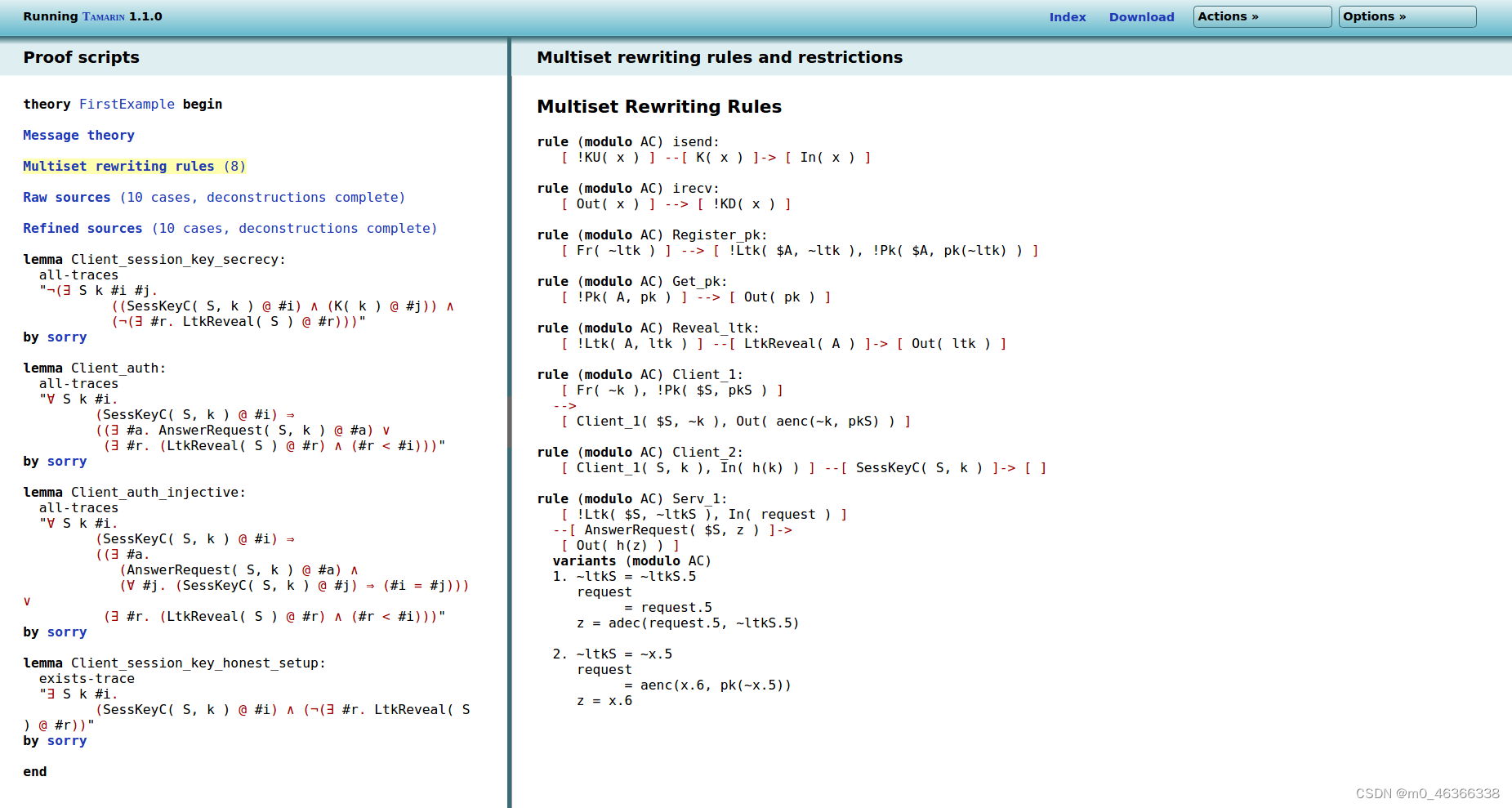
屏幕右侧是协议的重写规则,外加两条附加规则:isend 和 irecv2。这两条额外的规则为协议的输出和输入与对手演绎提供了接口。isend 规则接收一个事实 !KU(x),即对手知道的一个值 x,并将其传递给协议输入 In(x)。规则 irecv 接收协议输出 Out(x),并将其传递给对手的知识(由 !KD(x) 事实表示)。请注意,来自协议的规则 Serv_1 有两个变体(模数 AC)。这一点的确切含义现在并不重要(它源于 Tamarin 处理方程的方式),将在加密信息部分进行解释。
现在点击 “精炼来源”(10 个案例,解构完成),可以看到以下内容:
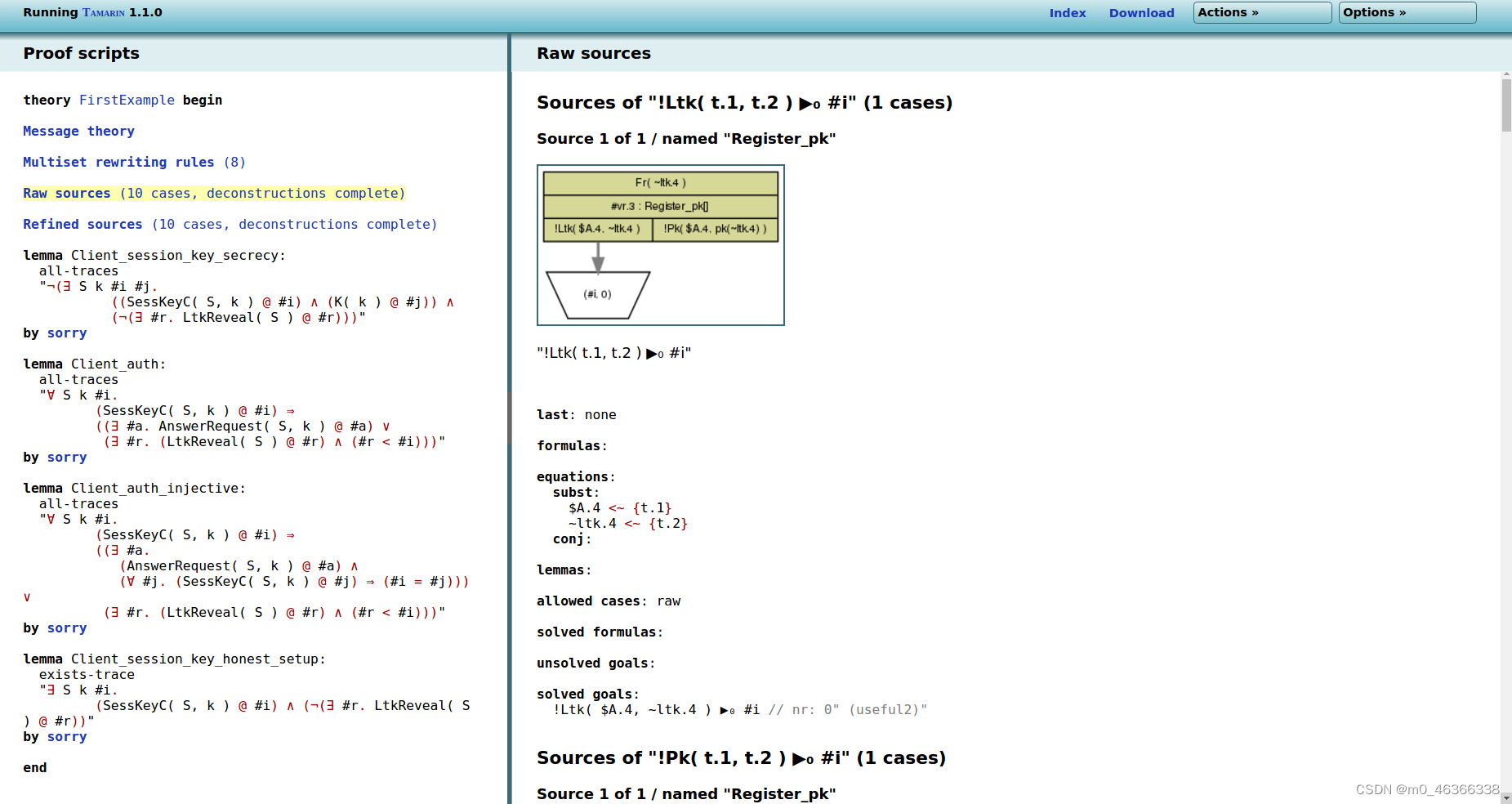
为了提高内部推理的效率,Tamarin 预先计算了案例区分。案例区分给出了某一事实的所有可能来源,即产生这一事实的所有规则(或规则组合),然后可用于 Tamarin 的后向搜索。这些情况区分用于避免重复计算相同的内容。右侧是 FirstExample 理论的预计算结果。
例如,塔马林在这里告诉我们,事实 !Ltk( t.1, t.2 ) 有一个可能的来源,即规则 Register_pk。图片显示了代表执行情况的(不完整)图。绿色方框代表 Register_pk 规则的实例,底部的梯形代表 !Ltk( t.1, t.2 ) 事实的 “汇”。这里的案例区分只包括一个规则实例,但案例区分内部可能有多个规则实例和多个案例,如下图所示。
图片下方给出的技术信息目前并不重要,它提供了关于如何计算案例区分的详细信息,以及是否还有其他约束条件(如等式或替换)需要解决。
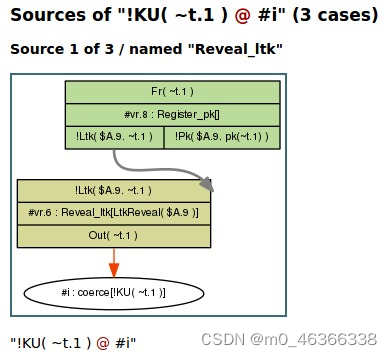
在这里,事实 !KU( ~t.1 ) 有三个来源,第一个是规则 Reveal_ltk,它需要规则 Register_pk 的实例来创建必要的 !Ltk 事实。其他两个来源如下。
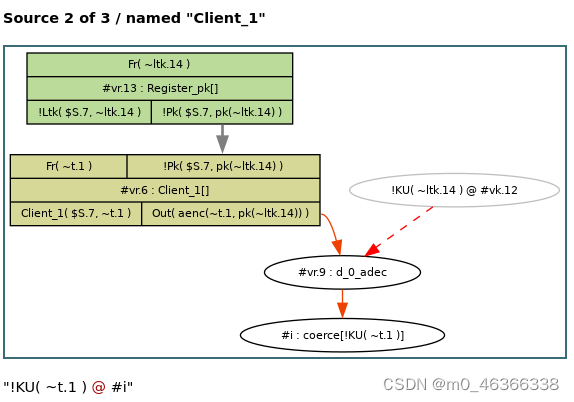

现在我们来看看如何在互动模式下证明公例。为此,请在左侧框架中的第一个 Lemma 之后点击 “抱歉”(表示尚未开始证明),以获得如下界面:
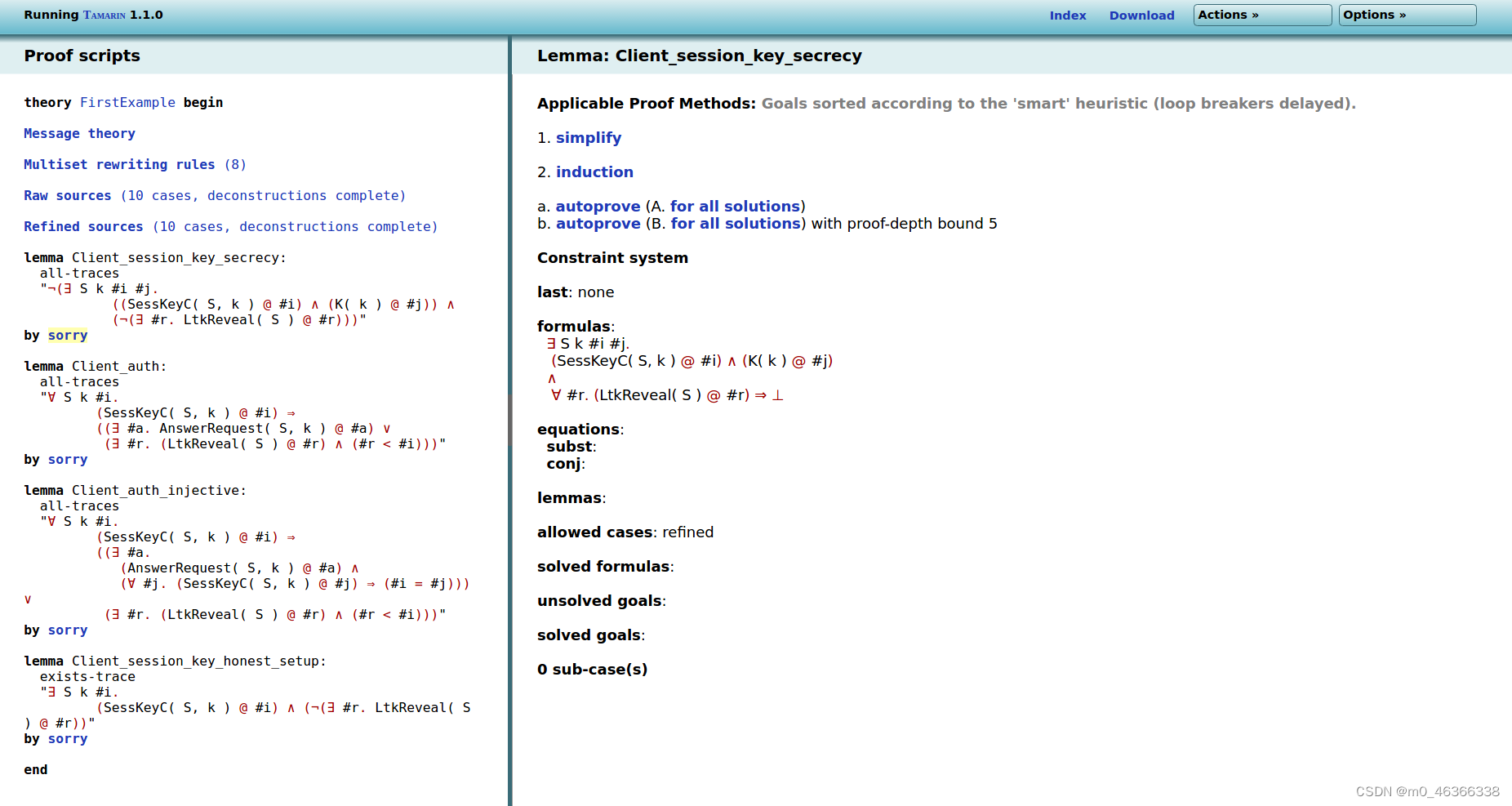
Tamarin 使用约束解法证明公例。也就是说,它会不断完善它所掌握的有关属性和协议的知识(称为约束系统),直到它能得出结论认为该属性在所有可能的情况下都成立,或者找到该定理的反例为止。
在右图中,我们可以看到最上面是可能的证明步骤,下面是约束系统的当前状态(由于尚未开始证明,所以是空的)。证明总是从简化步骤 (1. simplify) 或归纳设置步骤 (2. induction) 开始,前者将 Lemma 转化为需要解决的初始约束系统,后者则通过对轨迹长度的归纳生成证明 Lemma 所需的约束。在此,我们使用默认策略,即通过点击 1:

现在,Tamarin 已将该两难式转化为一个约束系统。由于 Tamarin 正在寻找该lemma 的反例,因此它会寻找包含 SessKeyC( S, k ) 和 K( k ) 操作,但没有使用 LtkReveal( S ) 的协议执行。这在图中可视化如下。获得 SessKeyC( S, k ) 操作的唯一方法是使用左侧的 Client_2 规则实例,而 K( k ) 规则在右侧使用圆方框表示(对手推理总是使用圆方框可视化)。就在图的下方,公式formulas: ∀ #r. (LtkReveal( S ) @ #r) ⇒ ⊥
现在,任何 LtkReveal( S ) 的出现都会导致矛盾。
要完成证明,我们可以手动选择下一步要解决的约束条件,或者调用自动证明命令,该命令会根据启发式选择下一步。在这里,我们有两个约束需要解决: Client_1( S, k ) 和 KU( k ),它们都是当前未完成的约束系统中规则的前提。
请注意,图形用户界面中的证明方法是根据与自动证明命令相同的启发式排序的。任何通过选择第一种证明方法找到的证明都将与自动证明命令构建的证明相同。不过,由于一般问题是不可判定的,因此算法可能不会对每个协议和属性都终止。
在本例中,无论是多次点击第一个约束条件,还是使用自动求证器,我们都以下面的最终状态结束,其中构建的图包含 LtkReveal( S ),从而导致矛盾:
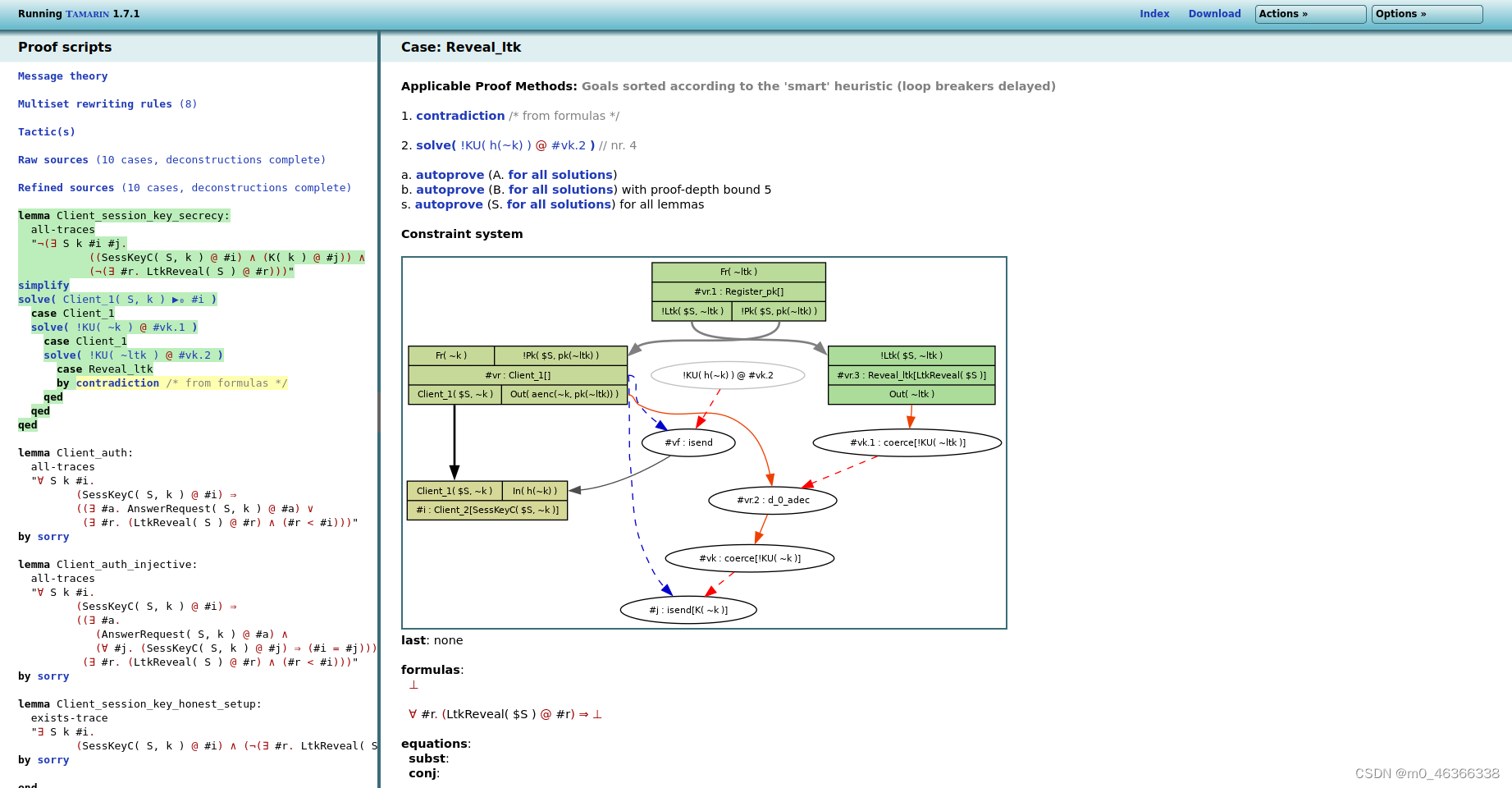
由于该 Lemma 已被成功证明,因此用绿色表示。如果我们发现了反例,则会用红色标出。你可以用同样的方法证明其他定理。
正如你可能已经注意到的,箭头可以有很多不同的类型,它们的颜色也各不相同。
有普通(实心)箭头(黑色或灰色),用来表示协议事实的起源(线性或持久事实)。还有实心红色橙色箭头,表示对手从收到的信息中提取值的步骤。
然后是虚线箭头,表示两个操作之间的排序限制,其颜色表示限制的原因:
- 黑色虚线箭头表示源于公式的排序约束,例如源于当前的 Lemma 或限制条件。
- 深蓝色表示由新鲜值推导出的排序约束:因为新鲜值是唯一的,所以所有使用新鲜值的规则实例都必须出现在创建该值的实例之后。
- 红色虚线箭头用于表示对手合成值的步骤。
- 深橙色代表 Tamarin 的正常形式条件所隐含的排序约束。
- 紫色表示源自注入式事实实例的排序约束,参见注入式实例。
虚线边可以同时使用多种颜色,这意味着同时存在多个排序约束。
例如,黑蓝相间的虚线箭头表示有两个约束条件:一个是从公式中推导出来的,另一个是从规则实例中出现的新值中推导出来的。
最后,在中间证明步骤中,还可能出现绿色虚线箭头,这在 Tamarin 的证明搜索过程中用来表示不完整的对手推导步骤。
请注意,默认情况下 Tamarin 不会显示所有规则和箭头,以简化图形,但可以通过页面右上角的选项按钮进行调整。
在命令行上运行 Tamarin
tamarin-prover FirstExample.spthy
该调用会解析 FirstExample.spthy 文件,检查其完备性,并漂亮打印理论。签名声明和方程可以在漂亮打印的理论顶端找到。
使用自动证明器证明理论中包含的所有定理,只需在调用中添加 --prove 标志即可;即
tamarin-prover FirstExample.spthy --prove
这将首先输出约束求解器的一些日志,然后输出 FirstExample 安全协议理论及其附带的(反)证明:
summary of summaries:analyzed: FirstExample.spthyClient_session_key_secrecy (all-traces): verified (5 steps)Client_auth (all-traces): verified (11 steps)Client_auth_injective (all-traces): verified (15 steps)Client_session_key_honest_setup (exists-trace): verified (5 steps)
可以通过多个–prove 标志和指定一个公共前缀后跟一个通配符来选择词素,例如:–prove=Client_auth*。注意:在大多数 shell 中,“*“需要转义为”*”。
警告后退出
正如 "图形用户界面 "中提到的,在较大的模型中,我们可能会漏掉格式错误(在编写 Tamarin 文件和运行 tamarin-prover 时):在许多情况下,网络服务器会正确启动,这使得我们更难注意到规则或词法中的错误。
为确保所提供的 .spthy 文件没有任何错误或警告(并在出现错误时停止预处理和其他计算),最好在命令行中使用 --quit-on-warning 标志。例如
tamarin-prover interactive FirstExample.spthy --quit-on-warning
这将阻止 Tamarin 的计算继续进行,并将导致 Tamarin 停止计算的错误或警告留在终端上。
完整示例
/*
Initial Example for the Tamarin Manual
======================================Authors: Simon Meier, Benedikt Schmidt
Updated by: Jannik Dreier, Ralf Sasse
Date: June 2016This file is documented in the Tamarin user manual.*/theory FirstExample
beginbuiltins: hashing, asymmetric-encryption// Registering a public key
rule Register_pk:[ Fr(~ltk) ]-->[ !Ltk($A, ~ltk), !Pk($A, pk(~ltk)) ]rule Get_pk:[ !Pk(A, pubkey) ]-->[ Out(pubkey) ]rule Reveal_ltk:[ !Ltk(A, ltk) ]--[ LtkReveal(A) ]->[ Out(ltk) ]// Start a new thread executing the client role, choosing the server
// non-deterministically.
rule Client_1:[ Fr(~k) // choose fresh key, !Pk($S, pkS) // lookup public-key of server]-->[ Client_1( $S, ~k ) // Store server and key for next step of thread, Out( aenc(~k, pkS) ) // Send the encrypted session key to the server]rule Client_2:[ Client_1(S, k) // Retrieve server and session key from previous step, In( h(k) ) // Receive hashed session key from network]--[ SessKeyC( S, k ) ]-> // State that the session key 'k'[] // was setup with server 'S'// A server thread answering in one-step to a session-key setup request from
// some client.
rule Serv_1:[ !Ltk($S, ~ltkS) // lookup the private-key, In( request ) // receive a request]--[ AnswerRequest($S, adec(request, ~ltkS)) ]-> // Explanation below[ Out( h(adec(request, ~ltkS)) ) ] // Return the hash of the// decrypted request.lemma Client_session_key_secrecy:" /* It cannot be that a */not(Ex S k #i #j./* client has set up a session key 'k' with a server'S' */SessKeyC(S, k) @ #i/* and the adversary knows 'k' */& K(k) @ #j/* without having performed a long-term key reveal on 'S'. */& not(Ex #r. LtkReveal(S) @ r))"lemma Client_auth:" /* For all session keys 'k' setup by clients with a server 'S' */( All S k #i. SessKeyC(S, k) @ #i==>/* there is a server that answered the request */( (Ex #a. AnswerRequest(S, k) @ a)/* or the adversary performed a long-term key reveal on 'S'before the key was setup. */| (Ex #r. LtkReveal(S) @ r & r < i)))"lemma Client_auth_injective:" /* For all session keys 'k' setup by clients with a server 'S' */( All S k #i. SessKeyC(S, k) @ #i==>/* there is a server that answered the request */( (Ex #a. AnswerRequest(S, k) @ a/* and there is no other client that had the same request */& (All #j. SessKeyC(S, k) @ #j ==> #i = #j))/* or the adversary performed a long-term key reveal on 'S'before the key was setup. */| (Ex #r. LtkReveal(S) @ r & r < i)))"lemma Client_session_key_honest_setup:exists-trace" Ex S k #i.SessKeyC(S, k) @ #i& not(Ex #r. LtkReveal(S) @ r)"end- 使用默认的 Tamarin 设置时,只有一个公共信道建模网络由对手控制,即对手从 Out( ) 事实中接收所有信息,并在 In( )
事实中生成协议输入。如有需要,还可以添加私人通道,详情请参见通道模型。 - i "在历史上源于 “入侵者”,但这里我们使用 “对手”。
加密信息
Tamarin 根据密码学的符号模型分析协议。这意味着加密信息被建模为术语而不是比特串。
所使用的加密算法的属性由方程建模。更具体地说,加密信息既可以是常数 c,也可以是信息 f(m1,…,mn),对应于对 n 个加密信息 m1, …, mn 应用 nary 函数符号 f。在指定等式时,除常量外,我们还允许使用变量。
常数
我们对这些常量类型进行了区分:
- 公共常量建模公众已知的原子信息,如代理身份和标签。我们使用 "ident "来表示 Tamarin 中的公共常量。这类常量属于 pub类型,因此可以与公共变量统一起来。对手总是知道这些常量的。
- 数元为 0 的函数(见下文)。函数的排序总是msg,因此不能与公有变量统一。默认情况下,该函数是公有的,且为对手所知。如果函数被声明为私有,则不会被对手知道。然而,新鲜值通常是秘密值的更合适模型。
- 自然数只有一个常数,其写法为 %1 或 1:nat,表示数字 1。
函数符号
Tamarin 支持一组固定的内置函数符号和额外的用户自定义函数符号。每个 Tamarin 文件中唯一可用的函数符号是配对和投影。二进制函数符号 pair 模拟两个信息的配对,函数符号 fst 和 snd 模拟第一个参数和第二个参数的投影。投影的特性由以下等式表示:
fst(pair(x,y)) = x
snd(pair(x,y)) = y
Tamarin 还支持 <x,y> 作为 pair(x,y) 的语法糖,以及 <x1,x2,…,xn-1,xn> 作为 <x1,<x2,…,<xn-1,xn>…> 的语法糖。
附加的内置函数符号可以通过包含以下信息理论之一来激活:散列、非对称加密、签名、揭示签名、对称加密、差分赫尔曼、双线性配对、xor 和多集。
要激活消息理论 t1、…、tn,请在文件中加入内置行:t1、…、tn。内置消息理论的定义在内置消息理论一节中给出。
要定义参数为 a1,…, an 的函数符号 f1, …, fn,请在文件中包含以下一行:
functions: f1/a1, ..., fn/an
Tamarin 还支持私有函数符号。与常规函数符号不同,Tamarin 假设对手无法应用私有函数符号。私有函数可用于对隐式使用所有(诚实)用户共享的秘密的函数进行建模。要使函数私有,只需在函数声明后添加属性 [private]。例如
functions: f/3, g/2 [private], h/1
定义了私有函数 g 以及公共函数 f 和 h。我们将在下一节中介绍如何定义公式来形式化函数的属性。
等式理论
等式理论可用于模拟函数的属性,例如,对称解密是对称加密的逆,只要两者使用相同的密钥。在上下文中添加等式的语法是
equations: lhs1 = rhs1, ..., lhsn = rhsn
lhs 和 rhs 都可以包含变量,但不能包含公共常量,右侧的所有变量也必须出现在左侧。Tamarin 使用的符号证明搜索支持某类用户定义的方程,即具有有限变式属性的收敛方程理论(Comon-Lundh 和 Delaune,2005 年)。请注意,Tamarin 不会检查给定的方程是否属于这一类,因此写入这一类之外的方程可能会导致不终止或结果不正确,而不会发出任何警告。
还要注意的是,Tamarin 的推理在只考虑子项收敛方程时特别有效,也就是说,如果右侧是一个基本项(即不包含任何变量)或左侧的一个适当子项。因此,如果这些方程足以模拟所需的性质,则应优先采用。然而,例如由内置信息理论 diffie-hellman、双线性配对、xor 和 multiset 建模的方程就不属于这个受限制的类别,因为它们包括关联性和交换性。所有其他内置信息理论都可以通过使用函数:…和方程:…来等价定义。
内置信息理论和其他内置功能
在下文中,我们用 f/n 表示函数符号 f 是 n 阶的。
散列:
该理论是哈希函数的模型。它定义了函数符号 h/1,没有方程。
非对称加密:
该理论模拟公钥加密方案。它定义了函数符号 aenc/2、adec/2 和 pk/1,它们之间的关系式为 adec(aenc(m, pk(sk)), sk) = m。请注意,如语法说明中所述,aenc{x,y}pkB 是 aenc(<x,y>, pkB) 的语法糖。
签名:
该理论是签名方案的模型。它定义了函数符号 sign/2、verify/3、pk/1 和 true,它们的关系式为 verify(sign(m,sk),m,pk(sk)) = true。
揭示-签名:
该理论是信息揭示签名方案的模型。它定义了函数符号 revealSign/2、revealVerify/3、getMessage/1、pk/1 和 true,它们之间的关系式为 revealVerify(revealSign(m,sk),m,pk(sk)) = true 和 getMessage(revealSign(m,sk)) = m。
对称加密:
该理论模拟对称加密方案。它定义了函数符号 senc/2 和 sdec/2,它们之间的关系式为 sdec(senc(m,k),k) = m。
Diffie-hellman:
该理论模拟 Diffie-Hellman 群。它定义了函数符号 inv/1、1/0 以及符号 ^ 和 *。我们用 g ^ a 表示群中的幂级数,用 *、inv 和 1 表示指数的(乘法)阿贝尔群(群阶的整数模)。定义方程组为
(x^y)^z = x^(y*z)
x^1 = x
x*y = y*x
(x*y)*z = x*(y*z)
x*1 = x
x*inv(x) = 1
双线性配对:
该理论以双线性群为模型。这里,pmult(x,p) 表示点 p 与标量 x 的乘法,em(p,q) 表示双线性映射对点 p 和 q 的应用:
pmult(x,(pmult(y,p)) = pmult(x*y,p)
pmult(1,p) = p
em(p,q) = em(q,p)
em(pmult(x,p),q) = pmult(x,em(q,p))
xor:
该理论模拟了排他运算。它添加了函数符号 ⊕/2(也写作 XOR/2)和零/0:
x ⊕ y = y ⊕ x
(x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
x ⊕ zero = x
x ⊕ x = zero
多集:
该理论引入了关联-交换运算符 ++,通常用于多集建模1。
自然数
该理论引入了关联交换运算符 %+ 和公共常量 %1,用于建立计数器模型。它还引入了排序 nat,变量可以用它来注释,就像排序 pub $: n:nat 或 %n。此外,运算符 %+ 只接受 nat 排序项,也是唯一能产生 nat 排序项的运算符。这保证了任何 nat 排序的项本质上都是 %1 的和。因此,所有自然数都是公共知识,这加快了 Tamarin 的运行速度,因为无需搜索数字的攻击者构造。
需要注意的是,这些 nat 项只适用于模拟小自然数,例如假设攻击者可以猜到的计数器。要模拟大的随机数,建议使用新变量。
在某些协议(如 WPA-2)中,大自然数会以随机起点的计数器形式增加。对于此类模型,建议使用一对 <~x,%n>,其中 ~x 是随机起始点,%n 是可猜测的计数器。
可靠信道:
该理论在流程微积分中引入了对可靠信道的支持。信道(即公共名称)'r’上的信息保证最终到达。只有另一个通道,即公共的不可靠通道 “c”。请注意,可以使用模式匹配来模拟多个可靠信道:
out('r',<'channelA','Hello')
| out('r',<'channelB','Bonjour')
| in('r',<'channelA',x); event PrepareTea()
| in('r',<'channelB',x); event PrepareCoffee()
保留函数符号名称
由于在内置报文理论中的使用,下列函数名不能由用户定义:mun、one、exp、mult、inv、pmult、em。
如果一个理论包含其中任何一个用户定义的函数符号,解析器将拒绝该文件,并说明重新声明了哪个保留名。
Comon-Lundh, Hubert, and Stéphanie Delaune. 2005. “有限变量属性: 如何摆脱某些代数属性”。见《RTA》,294-307。
五、使用规则进行模型规范
在本节中,我们将对基本模型进行非正式描述。该模型的全部细节可参见(施密特,2012 年)。
Tamarin 模型由三个主要部分组成:
1.规则(Rules)
2.事实(Facts)
3.术语(Terms)
我们已经在上一节中了解了术语的定义。下面我们将讨论事实和规则,并以 Naxos 协议(认证密钥交换协议)为例说明它们的使用,如下所示。
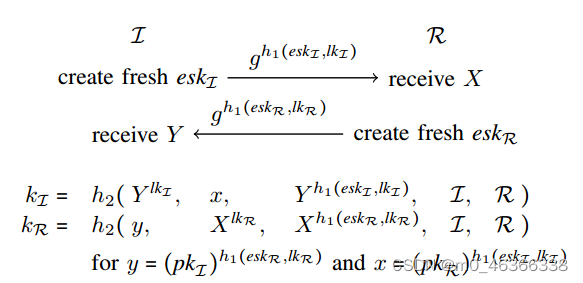
在这个协议中,每一方 x 都有一个长期私人密钥 lkx 和一个相应的公开密钥 pkx = ‘g’^lkx,其中’g’是 Diffie-Hellman 群的一个生成器(密钥生成器)。因为’g’可以是公开的,所以我们将其建模为一个公共常数。我们使用两种不同的哈希函数 h1 和 h2。
Diffie-Hellman (DH) 组确定了在密钥交换进程中使用的密钥的强度。 组的编号越大安全性就越高,但是也就需要更多的时间来计算密钥。
哈希 其实是随机存储的一种优化,先进行分类,然后查找时按照这个对象的分类去找。哈希通过一次计算大幅度缩小查找范围,自然比从全部数据里查找速度要快。
哈希函数
哈希的过程中需要使用哈希函数进行计算。
哈希函数是一种映射关系,根据数据的关键词 key ,通过一定的函数关系,计算出该元素存储位置的函数。
表示为:
address = H [key]
启动会话时,发起者 I 首先创建一个新的随机数 eskI,也就是 I 的短暂(私人)密钥。然后,他将 eskI 与 I 的长期私人密钥 lkI 相连,使用散列函数 h1 对结果进行散列,并将’g’^h1(eskI ,lkI)发送给应答者。响应者 R 将接收到的值存储在变量 X 中,然后根据自己的非密钥 eskR 和长期私人密钥 lkR 计算出一个类似的值,并将结果发送给发起者,发起者将接收到的值存储在变量 Y 中。最后,双方分别计算出一个会话密钥(kI 和 kR),其计算包括各自的长期私人密钥,这样只有目标伙伴才能计算出相同的密钥。
Nonce,Number used once或Number once的缩写,在密码学中Nonce是一个只被使用一次的任意或非重复的随机数值,在加密技术中的初始向量和加密散列函数都发挥着重要作用,在各类验证协议的通信应用中确保验证信息不被重复使用以对抗重放攻击(Replay Attack)。在信息安全中,Nonce是一个在加密通信只能使用一次的数字。在认证协议中,它往往是一个随机或伪随机数,以避免重放攻击。Nonce也用于流密码以确保安全。如果需要使用相同的密钥加密一个以上的消息,就需要Nonce来确保不同的消息与该密钥加密的密钥流不同。
需要注意的是,交换的信息并没有经过身份验证,因为接收方无法验证在构建信息时是否使用了预期的长期密钥。认证是隐式的,只有通过拥有正确的密钥才能保证。在认证密钥交换协议中,通常通过添加密钥确认步骤来实现显式认证(例如,目标伙伴最近还活着或同意某些值),在这一步骤中,双方交换交换信息的 MAC,该 MAC 使用计算会话密钥的(变种)密钥。
规则
我们使用多集重写来指定协议和对手的并发执行。**多集重写是一种常用的并发系统建模形式,**因为它天然支持独立的转换。
多重集重写MSR(multiset rewriting)模型是一种基于多重集重写的协议形式化建模方法.
多集重写系统定义了一个转换系统,在我们的例子中,转换将被标记。系统的状态是事实的多集(袋)。下面我们将解释事实的类型及其用途。
Tamarin 中的重写规则有一个名称和三个部分,每个部分都是一系列事实:
- 一个是规则的左侧事实
- 一个是标注转换的事实(我们称之为 “动作事实”)
- 还有一个是规则的右侧事实。例如
rule MyRule1:[ ] --[ L('x') ]-> [ F('1','x'), F('2','y') ]rule MyRule2:[ F(u,v) ] --[ M(u,v) ]-> [ H(u), G('3',h(v)) ]
目前,我们将忽略动作事实(L( …) 和 M(…)),在下一节讨论属性时再回到它们。如果一条规则没有标注动作事实,箭头符号–[ ]-> 可以缩写为–>。
规则名称仅用于引用特定规则。它们没有特定含义,可以任意选择,只要每条规则都有一个唯一的名称即可。
执行
过渡系统的初始状态是空多集合。
规则定义了系统如何过渡到新的状态。如果一条规则可以被实例化,使其左侧事实包含在当前状态中,那么它就可以被应用于一个状态。在这种情况下,左侧事实会从状态中移除,并被实例化的右侧事实所取代。
例如,在初始状态中,MyRule1 可以被重复实例化。
对于 MyRule1 的任何实例化,都会导致包含 F(‘1’,‘x’) 和 F(‘2’,‘y’) 的后续状态。由于 MyRule2 不包含 F 事实,因此无法应用于初始状态。在后续状态中,规则 MyRule2 现在可以应用两次。它的实例化可以是 u 等于’1’(v 等于’x’)或’2’(v 等于’y’)。每个实例都会产生一个新的后续状态。
在本地宏的规则中使用 "let "绑定
在为更复杂的协议建模时,一个术语可能会在同一规则中出现多次(可能作为子术语)。为使此类规范更易读,Tamarin 提供了 let ... in 支持,如下例所示:
rule MyRuleName:let foo1 = h(bar)foo2 = <'bars', foo1>...var5 = pk(~x)in[ ... ] --[ ... ]-> [ ... ]
这种 let 绑定表达式可用于在规则上下文中指定本地术语宏。每个宏应单独成行,并定义一个替换:= 符号的左侧必须是一个变量,右侧是一个任意项。规则将在用let中出现的所有变量的右侧进行替换后进行解释。如上例所示,宏可以使用先前定义的宏的左手边。
### 全局宏 {#sec:macros}
有时,我们希望在多个规则中使用相同的 let 约束。在这种情况下,我们可以使用 macros 关键字定义全局宏,它适用于所有规则。请看下面的例子
**macros: macro1(x) = h(x), macro2(x, y) = <x, y>, ..., macro7() = $A**
这里,macro1 是第一个宏的名称,x 是它的参数。第二个宏叫 macro2,有两个参数 x 和 y。最后一个宏 macro7 没有参数。= 符号右边的项是宏的输出。它可以是由等式理论中定义的函数和宏的参数构成的任何项。
在规则中使用宏时,我们可以像在术语中使用函数一样使用宏。例如
[ In(macro1(~ltk)) ] --[ ... ]-> [ Out(macro2(pkA, pkB)) ]
将成为
[ In(h(~ltk)) ] --[ ... ]-> [ Out(<pkA, pkB>) ]
在应用了上述宏之后。
一个宏可以调用第二个宏,如果第二个宏是在宏定义之前定义的。例如,可以定义以下两个宏:
macros: innerMacro(x, y) = <x, y>, hashMacro(x, y) = h(innerMacro(x, y))
但是,以下代码段会导致错误
macros: hashMacro(x, y) = h(innerMacro(x, y)), innerMacro(x, y) = <x, y>
因为在定义 hashMacro 时,innerMacro 尚未定义。
宏只适用于规则,并在交互模式下与协议规则一起显示。导出理论时,Tamarin 将导出原始规则(应用宏之前)和宏。
事实
事实符号 F 和术语 ti 的形式为 F(t1,…,tn)。它们有一个固定的词性(在本例中为 n)。需要注意的是,如果 Tamarin 模型使用了具有两个不同词性的同一事实,Tamarin 将报错。(?)
Tamarin 内置了三种特殊事实。这些事实用于模拟与不受信任网络的交互,以及模拟唯一新鲜(随机)值的生成。
In
该事实用于模拟一方从不受信任的网络中接收由 Dolev-Yao 对手控制的信息,并且只能出现在重写规则的左侧。
Out
该事实用于模拟由 Dolev-Yao 对手控制的向不受信任网络发送信息的一方,只能出现在重写规则的右侧。
Fr
这一事实必须在生成新值(随机值)时使用,而且只能出现在重写规则的左侧,其参数就是新项。Tamarin 的底层执行模型内置了生成 Fr(x) 事实实例的规则,并确保每个实例生成的术语(实例化 x)都与其他所有术语不同。
对于上述三个事实,Tamarin 有内置的规则。特别是,有一条新规则可以生成唯一的 Fr(…) 事实,还有一组用于推导对抗知识的规则,这些规则消耗 Out(…) 事实并生成 In(…) 事实。
线性事实与持久事实
上述事实被称为 “线性事实”。它们不仅由规则产生,也可以被规则消耗。因此,它们可能会出现在一个状态中,但不会出现在下一个状态中。
相反,在我们的模型中,有些事实一旦被引入,就永远不会从状态中移除。如果使用线性事实来建模,就要求每条规则的左侧都有这样一个事实,而右侧也有这个事实的精确副本。虽然这种建模方式在理论上没有根本性的问题,但却给用户带来了不便,而且还可能导致 Tamarin 在实践中探索与追踪此类事实无关的规则实例,甚至可能导致无法终止。
基于以上两个原因,我们现在引入 “持久事实”,它们永远不会从状态中删除。我们用 “砰”(!)来表示这些事实。
事实总是以大写字母开头,无需明确声明。如果**事实名称的前缀是感叹号 !,那么它们就是持久的。**否则,它们就是线性的。需要注意的是,每个事实名称的使用都必须保持一致,即必须始终使用相同的弧度、大小写、持久性和多重性。否则,Tamarin 会抱怨该理论没有形成。
比较线性行为和持久事实行为,我们可以发现,如果某个规则的前提中存在持久事实,那么 Tamarin 会将所有在结论中产生该持久事实的规则视为源规则。但通常这样的规则很少(通常只有一条),这就简化了推理。对于线性事实,尤其是那些在许多规则中都会用到(并保持静态)的事实,显然有许多规则(所有规则!)都会在其结论中包含该事实。因此,当在任何前提中寻找来源时,都需要考虑所有这样的规则,这显然效率较低,而且如上所述不容易终止。因此,在对从未被消耗的事实进行建模时,最好使用持久事实。
嵌入式限制
在模拟协议时经常用到的一个技巧是,一旦调用了某条规则,就对跟踪执行限制,例如,如果该规则所代表的步骤需要在稍后的某个时间点执行另一个步骤,例如,模拟可靠信道。我们稍后会解释什么是限制,但粗略地说,它们指定了协议执行应遵守的约束条件。
这可以通过手工方式完成,即指定一个指代该规则所独有的行动事实的限制条件,或者像这样使用嵌入式限制条件:
rule B:[In(x), In(y)] --[ _restrict( formula )]-> []
其中公式为限制条件。请注意,嵌入式限制条件目前只能在跟踪模式下使用。
建模协议
安全协议的执行有多种定义方式,例如(Cremers 和 Mauw,2012 年)。在 Tamarin 中,没有预先定义的协议概念,用户可根据自己的选择自由建模。下面我们将举例说明如何对协议进行建模,并讨论之后的替代方案。
公钥基础设施
在 Tamarin 模型中,没有预先定义的公钥基础设施(PKI)概念。可通过一条为一方生成密钥的规则来模拟一个预先分布的 PKI,该 PKI 的每一方都有非对称密钥。当事人的身份和公钥/私钥作为事实存储在状态中,以便协议规则检索。对于公钥,我们通常使用 Pk 事实,对于相应的长期私钥,我们使用 Ltk 事实。由于这些事实只会被其他规则用来检索密钥,而不会被更新,因此我们将它们建模为持久事实。我们使用抽象函数 pk(x) 来表示与私钥 x 相对应的公钥,从而得出以下规则。请注意,我们也直接将所有公钥交给攻击者,右侧的 Out 表示攻击者。
rule Generate_key_pair:[ Fr(~x) ]-->[ !Pk($A,pk(~x)), Out(pk(~x)), !Ltk($A,~x)]
有些协议,如 Naxos,依赖于密钥对的代数特性。在许多基于 DH 的协议中,公钥为 gx,为私钥 x,这样就可以利用指数的交换性来建立密钥。在这种情况下,我们采用以下规则。
rule Generate_DH_key_pair:[ Fr(~x) ]-->[ !Pk($A,'g'^~x), Out('g'^~x), !Ltk($A,~x)]
模拟协议步骤
协议描述了系统中代理的行为。代理可以执行协议步骤,如接收信息并通过发送信息做出响应,或启动会话。
Naxos响应者角色建模
我们首先对响应者角色建模,这比发起者角色简单,因为只需一条规则即可完成。
该协议使用 Diffie-Hellman 指数,以及我们必须声明的两个哈希函数 h1 和 h2。我们可以使用:
builtins: diffie-hellman
和
functions: h1/1
functions: h2/1
无需任何进一步的公式,以这种方式声明的函数将作为单向函数运行。
每次代理 $R 的响应线程收到一条消息时,都会生成一个新值 ~eskR,发送一条响应消息,并计算一个密钥 kR。我们可以通过在规则左侧指定一个 In 事实来模拟接收消息的过程。为了对新鲜值的生成进行建模,我们要求它由内置的新鲜规则生成。
最后,该规则取决于行为者的长期私人密钥,我们可以从前面介绍的生成_DH_key_pair 规则生成的持久事实中获取该密钥。
响应信息是 g 乘以哈希函数的幂级数。由于哈希函数是一元函数(arity one),如果我们想在两个消息的连接中调用它,我们可以将它们建模为一对 <x,y>,并将其用作 h1 的单参数。
因此,这条规则的初始形式化可以如下:
rule NaxosR_attempt1:[In(X),//接收到XFr(~eskR),//生成新鲜随机数eskR!Ltk($R, lkR)//持久事实,$R的长期私人密钥]-->[Out( 'g'^h1(< ~eskR, lkR >) )//向$I发送信息]
不过,应答者也会计算一个会话密钥 kR。由于会话密钥不会影响发送或接收的信息,我们可以在规则的左侧和右侧省略它。不过,稍后我们要在安全属性中对会话密钥做出说明。因此,我们在操作中添加了计算密钥:
rule NaxosR_attempt2:[In(X),Fr(~eskR),!Ltk($R, lkR)]--[ SessionKey($R, kR ) ]->//计算会话密钥[Out( 'g'^h1(< ~eskR, lkR >) )]
上文尚未明确 kR 的计算方法。我们可以用 kR 的完整展开来替换上述规则中的 kR,但这样会降低可读性。相反,我们使用let绑定来避免重复并减少可能的不匹配。此外,为了计算密钥,我们需要通信伙伴 $I 的公钥,并将其与唯一的线程标识符 ~tid 绑定;我们将使用由此产生的行动事实来指定安全属性,这将在下一节中介绍。这将导致
rule NaxosR_attempt3:letexR = h1(< ~eskR, lkR >)//先定义exR,后面会用到(简化)hkr = 'g'^exR//向I发送的消息kR = h2(< pkI^exR, X^lkR, X^exR, $I, $R >)//会话密钥in[In(X),Fr( ~eskR ),Fr( ~tid ),!Ltk($R, lkR),!Pk($I, pkI)//持久事实,$I的公钥]--[ SessionKey( ~tid, $R, $I, kR ) ]->[Out( hkr )]
上述规则准确地模拟了应答者的角色,并计算出相应的密钥。
我们注意到还有一项优化有助于 Tamarin 的逆向搜索。在 NaxosR_attempt3 中,规则规定 lkR 可以与任何术语实例化,因此也包括非新鲜术语。然而,由于密钥生成规则是产生 Ltk 事实的唯一规则,而且它将始终使用新鲜的密钥值,因此很明显,在系统的任何可达状态下,lkR 只能由新鲜值实例化。因此,我们可以将 lkR 标记为新鲜类型,从而用 ~lkR 代替它。
rule NaxosR:let exR = h1(< ~eskR, ~lkR >)hkr = 'g'^exRkR = h2(< pkI^exR, X^~lkR, X^exR, $I, $R >)in[In(X),Fr( ~eskR ),Fr( ~tid ),!Ltk($R, ~lkR),!Pk($I, pkI)]--[ SessionKey( ~tid, $R, $I, kR ) ]->[Out( hkr )]
上述规则足以模拟基本的安全属性,我们稍后会看到。
Naxos启动器角色建模
Naxos 协议的发起者角色包括发送信息和等待响应。在启动者等待响应期间,其他代理也可能执行一些步骤。因此,我们使用两条规则对发起者进行建模。
第一条规则模拟一个代理启动发起者角色,生成一个新值,并发送相应的消息。和以前一样,我们使用 let 绑定来简化表述,并使用 ~lkI 代替 lkI,因为我们知道 !Ltk 事实只有在有新值作为第二个参数时才会产生。
rule NaxosI_1_attempt1:let exI = h1(<~eskI, ~lkI >)hkI = 'g'^exIin[ Fr( ~eskI ),!Ltk( $I, ~lkI ) ]-->[ Out( hkI ) ]
利用状态事实来模拟进展
触发前一条规则后,启动程序将等待响应信息。我们还需要对第二部分进行建模,即接收响应并计算密钥。要对启动器规则的第二部分进行建模,我们必须能够指定第一部分之前的规则和特定参数。直观地说,我们必须在转换系统的状态中存储这样一个信息:有一个启动线程已使用特定参数执行了第一次发送,因此它可以继续上次的操作。
为了建立这个模型,我们引入了一个新的事实,我们通常称之为状态事实:一个表明某个进程或线程正处于其执行过程中的某个特定点的事实,它实际上既是程序计数器,也是进程或线程内存内容的容器。由于可以并行存在任意数量的启动程序,我们需要为每个启动程序的状态事实提供唯一的句柄。
下面,我们将提供启动程序第一条规则的更新版本,它将产生一个状态事实 Init_1,并为该规则的每个实例引入一个唯一的线程标识符 ~tid。
rule NaxosI_1:let exI = h1(<~eskI, ~lkI >)hkI = 'g'^exIin[ Fr( ~eskI ),Fr( ~tid ),!Ltk( $I, ~lkI ) ]-->[ Init_1( ~tid, $I, $R, ~lkI, ~eskI ),Out( hkI ) ]
请注意,状态事实有几个参数:唯一的线程标识符 ~tid、代理身份 $I 和 $R、代理的长期私人密钥 ~lkI 和私人指数。这样,我们就可以指定第二条启动规则了。
rule NaxosI_2:letexI = h1(< ~eskI, ~lkI >)kI = h2(< Y^~lkI, pkR^exI, Y^exI, $I, $R >)in[ Init_1( ~tid, $I, $R, ~lkI , ~eskI),!Pk( $R, pkR ),In( Y ) ]--[ SessionKey( ~tid, $I, $R, kI ) ]->[]
第二条规则要求从网络中接收到一条信息 Y,同时还要求先前已生成了一条发起者事实。然后,该规则消耗该事实,由于协议中没有其他步骤,因此无需输出类似的事实。由于 Init_1 事实是用相同的参数实例化的,因此第二步将使用相同的代理身份和第一步计算出的指数 exI。
这样,完整的示例就变成了
theory Naxos
beginbuiltins: diffie-hellmanfunctions: h1/1
functions: h2/1rule Generate_DH_key_pair:[ Fr(~x) ] --> [ !Pk($A,'g'^~x), Out('g'^~x), !Ltk($A,~x)]rule NaxosR:let exR = h1(< ~eskR, ~lkR >)hkr = 'g'^exRkR = h2(< pkI^exR, X^~lkR, X^exR, $I, $R >)in[In(X),Fr( ~eskR ),Fr( ~tid ),!Ltk($R, ~lkR),!Pk($I, pkI)]--[ SessionKey( ~tid, $R, $I, kR ) ]->[Out( hkr )]rule NaxosI_1:let exI = h1(<~eskI, ~lkI >)hkI = 'g'^exIin[ Fr( ~eskI ),Fr( ~tid ),!Ltk( $I, ~lkI ) ]-->[ Init_1( ~tid, $I, $R, ~lkI, ~eskI ),Out( hkI ) ]rule NaxosI_2:letexI = h1(< ~eskI, ~lkI >)kI = h2(< Y^~lkI, pkR^exI, Y^exI, $I, $R >)in[ Init_1( ~tid, $I, $R, ~lkI , ~eskI),!Pk( $R, pkR ),In( Y ) ]--[ SessionKey( ~tid, $I, $R, kI ) ]->[]end
请注意,
**协议描述只指定了一个模型,而没有说明它可能满足哪些属性。**我们将在下一节讨论这些属性。
Cremers, Cas, and Sjouke Mauw. 2012. 安全协议的操作语义与验证》。Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-3-540-78636-8.
Schmidt, Benedikt. 2012. "密钥交换协议和物理协议的形式分析》。苏黎世联邦理工学院博士论文。http://dx.doi.org/10.3929/ethz-a-009898924.
这篇关于tamarin-manual(一到五)20230926271007的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!

![[SWPUCTF 2021 新生赛]web方向(一到六题) 解题思路,实操解析,解题软件使用,解题方法教程](https://i-blog.csdnimg.cn/direct/bcfaab8e5a68426b8abfa71b5124a20d.png)





