2021年北师大人工智能学院夏令营上机测试题解

前言:

有幸拿到rk1,但由于服务器卡成OI赛制,少A整整一道题。

这里多吐槽一句，连我们学校校内软卓选拔都舍得开一个月600的云服务器(当时我负责的这事儿)。北师大也太勤俭持家了吧,弄两天弹性服务也成啊呜呜呜

面试:

感觉凉透了，老师一直在问我rk能保研不(双非低rk的伤)。然后英语问答也没准备好，让介绍家乡，我就憋了三句话(我感觉让我用中文说，也就能说三句话).还是要多准备模板啊！！！

7.14号更新:拿到北师大offer了~北师大yyds啊

A.签到题(略)

B.数列比较

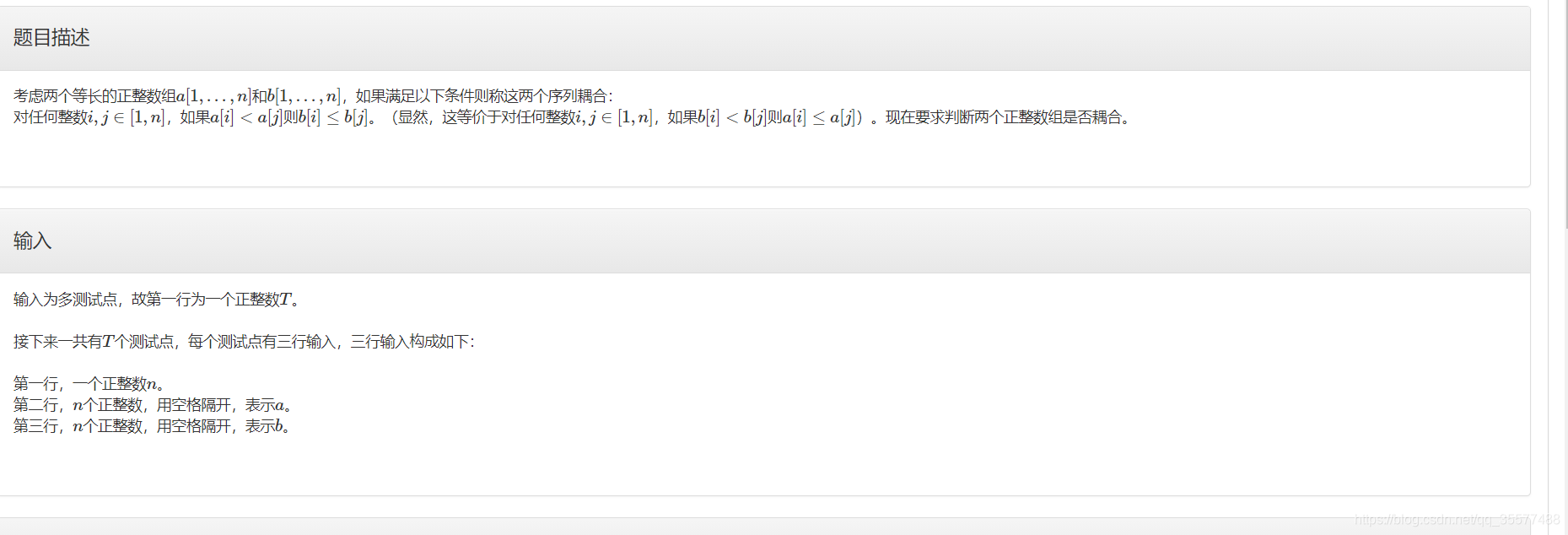
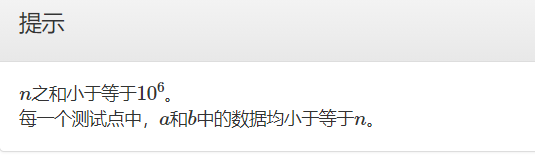
题目思路:

将a,b数组对应的存成点对。对第一维度(a)升序排序,那么条件转化为:
$当a[i]>a[i-1]$时，必须有$b[i]\ge b[j],j\in [1,i-1]$.即$b[i]\ge {\max }_{j=1}^{i-1}b[j]$.

所以根据我们的条件,对第一维排序，当相等的时候，对第二维升序排序。

这么排完后，我们只需要$O(n)$的$check$一遍第二维是否非降即可。

时间复杂度:$O(nlogn)$

C矩阵乘法

$n\le 100$

题目思路:

就枚举$a,b,c,d$,强行解方程完事了，有点无聊的题目。当然，我还被卡常了，打了个表过了。

时间复杂度:$O(n^4)$

D.猴子打字

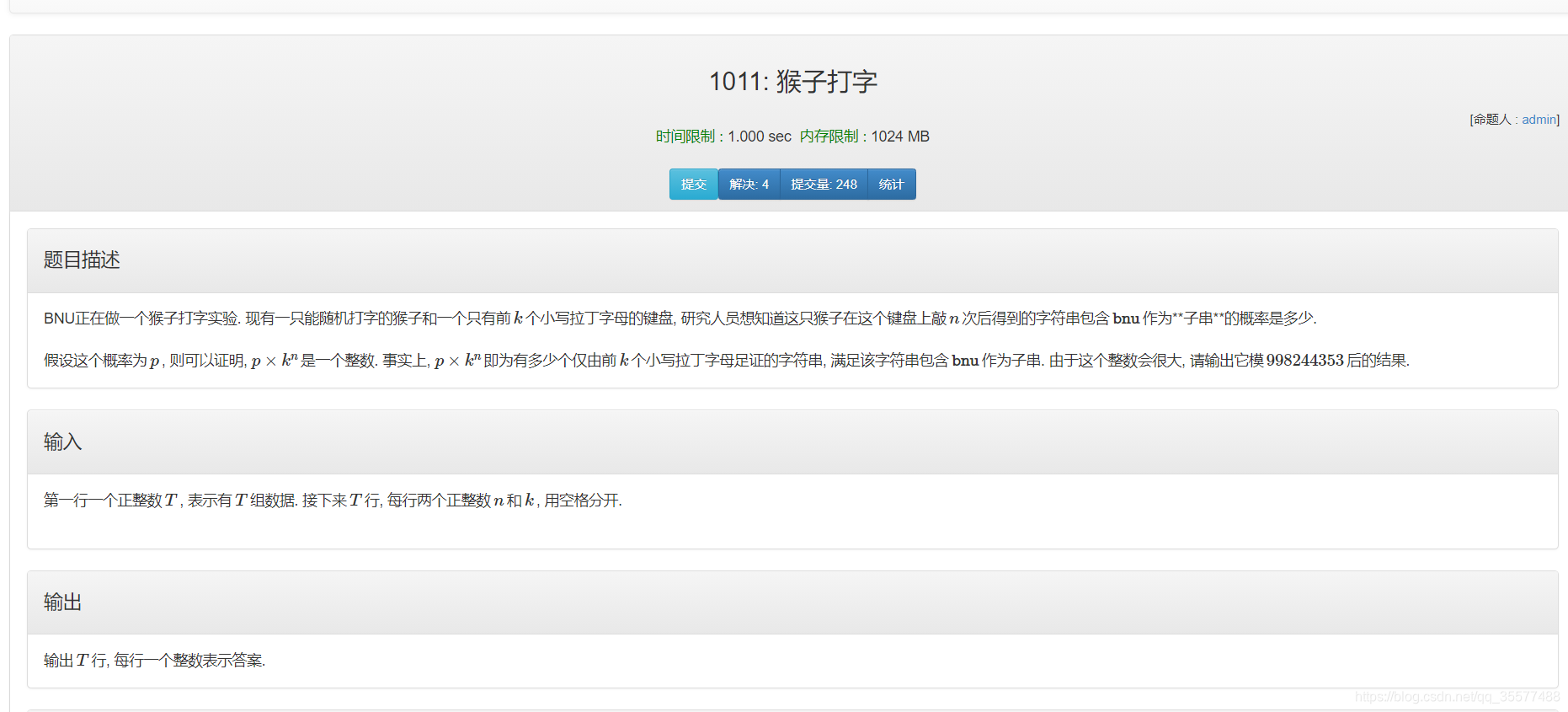
题目思路:

经典题目，我tm还能推错转移方程，自撒算了我靠。

不懂怎么做这题的，推荐看我这篇博客的第3题，把状态机思想弄明白

$n\le 90\%$的做法:状态机$dp$.

令$dp(i,j=0/1/2/3)$ 代表前$i$个长度,并且当前以状态$j$结尾的方案数.

$j=0$代表当前没出现$bnu$,且结尾也不是$b$.

$j=1$代表当前没出现$bnu$,且结尾恰好是$b$.

$j=2$代表当前没出现$bnu$,且结尾恰好是$bn$.

$j=3$代表当前已经出现了$bnu$.

PS:这么定义状态是因为$bnu$子串的出现一定是如上述按若干个小阶段构造出来的。

此时可以构建出有限状态机出来。状态的转移就像在图上游走。

如下图所示:

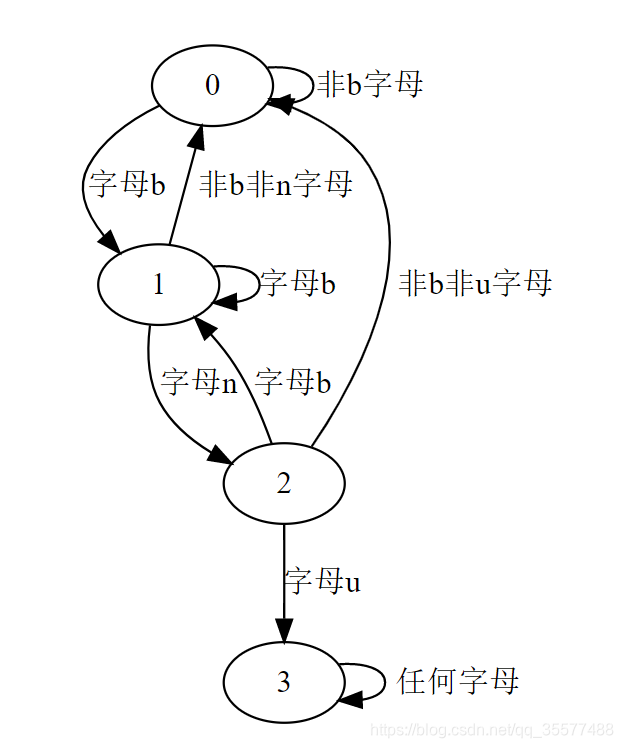
那么状态转移方程直接对着图推就好了:

$dp(i,0)=dp(i-1,0)\ast (k-1)+dp(i-1,1)\ast (k-2)+dp(i-1,2)\ast (k-2)$
$dp(i,1)=dp(i-1,0)+dp(i-1,1)+dp(i-1,2)$
$dp(i,2)=dp(i-1,1)$
$dp(i,3)=dp(i-1,2)+dp(i-1,3)\ast k$

$n=1e7$时,开滚动数组优化空间即可.

满分做法:矩阵快速幂优化dp

这只要会矩阵快速幂优化fib递推式就可以了.

so,对于上面的转移方程，我们将没有的项补0可以构造出下面的矩阵递推式:

令转移矩阵为:$T=\left(\begin{array}{cccc}k-1& k-2& k-2& 0\\ 1& 1& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 1& k\end{array}\right)$.

那么有:
$\left(\begin{array}{c}dp(n,0)\\ dp(n,1)\\ dp(n,2)\\ dp(n,3)\end{array}\right)=T\left(\begin{array}{c}dp(n-1,0)\\ dp(n-1,1)\\ dp(n-1,2)\\ dp(n-1,3)\end{array}\right)=T^n\left(\begin{array}{c}dp(0,0)\\ dp(0,1)\\ dp(0,2)\\ dp(0,3)\end{array}\right)=T^n\left(\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right)$

所以答案:$ans=T^n[4][1]$.

直接矩阵快速幂就好了~~

时间复杂度:$O(4^{3}logn)$

D.春游

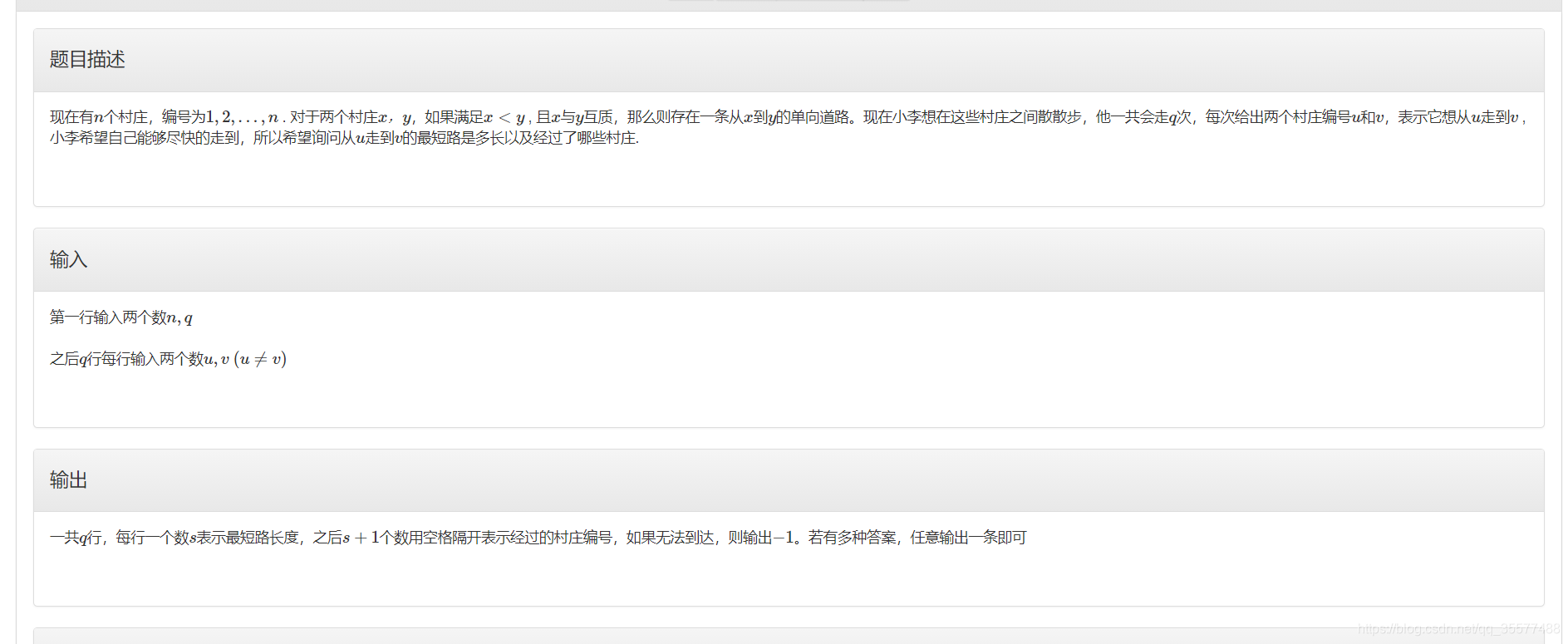
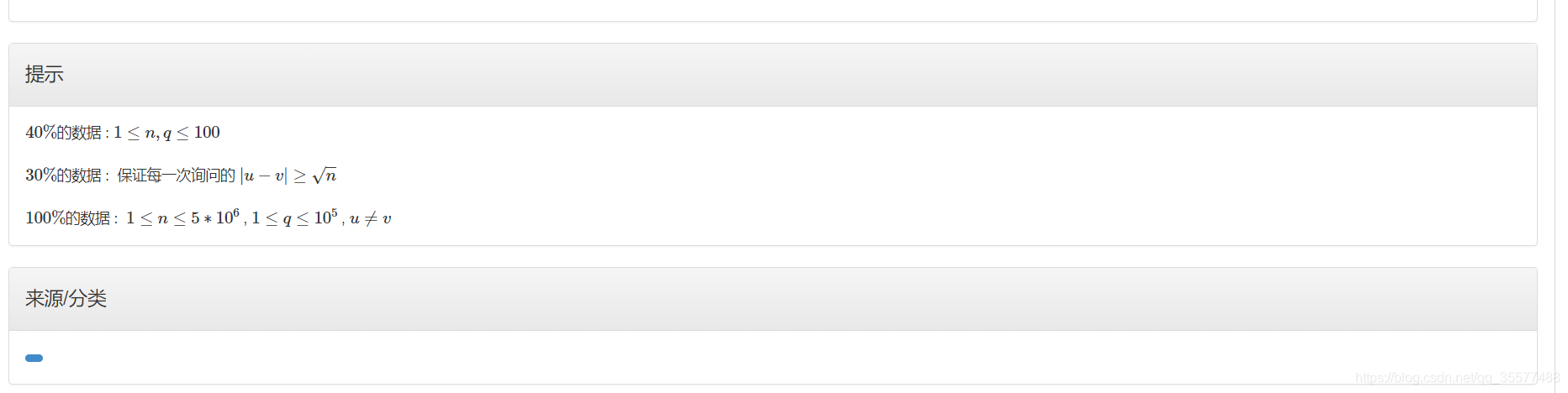
题目思路:

$40\%$的数据我直接bfs加输出路径了.

$30\%$的数据，直接$[u+1,v]$之间找一个不是$v$的约数的素数。(把素数筛出来，二分u后枚举素数)。这样确实非常快，但是没有正确性。总之是乱搞的。

满分做法待补~~