地震勘探——相关概念（一）

地震波的基本介绍

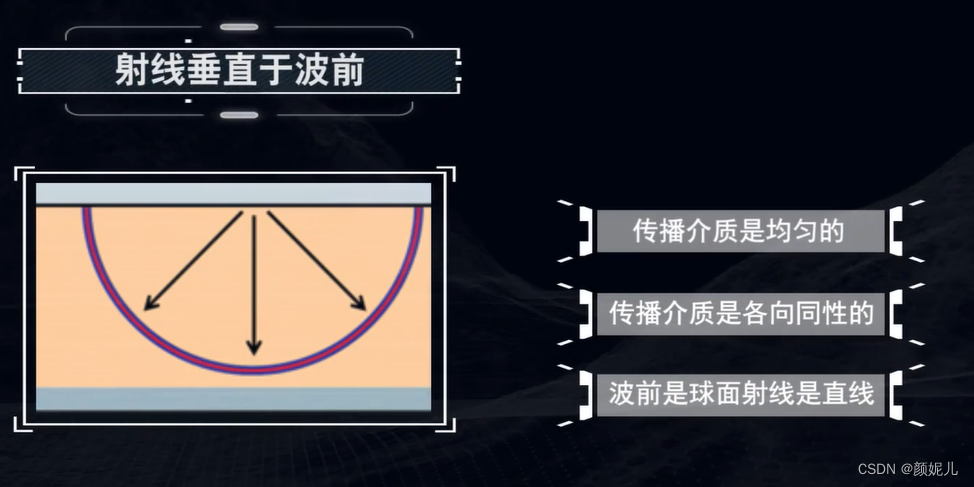
波前：波在同一时刻所到达的点所构成的面，这个面上构成的相位是相同的。波前的形状取决于传播介质的物理性质。我们可以用地震波动方程模拟波前变化（波场快照）。

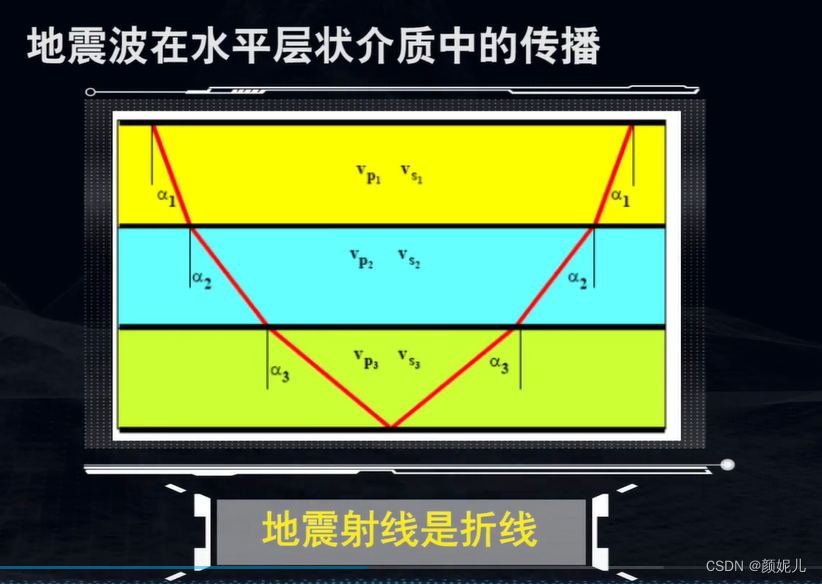
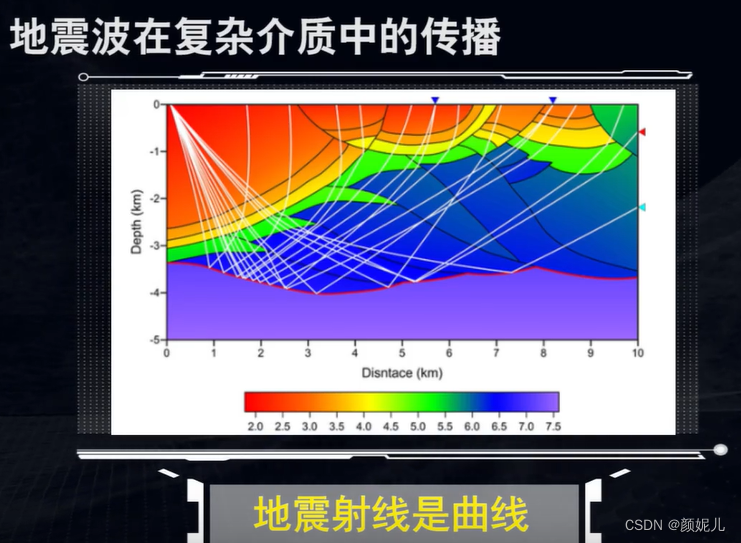
射线（Ray）：是一条假想的“线”，垂直于波前。射线指明了波的传播方向，但不能反映地震波的能量变化。射线的形状取决于地下岩层的性质。

惠更斯原理和费马原理

地震波在传播过程中遵循惠更斯原理和费马原理。
惠更斯原理：对于任何一种波，其波前上的任何一点都可以作为子波的波源，各个子波波源波前的包络面就是下一个波的波前。（一个波阵面的每个点可各看做是一个产生球面子波的次级球面波的中心波源，次级波源的波速与频率等于初级波的波速与频率；而且，以后任何时刻波阵面的位置是所有这种子波的包络面。这个结果实质上是“光学平行”面的一个作图法则，所以有时叫做惠更斯作图法。）
包络面：在波的传播过程中，总可以找到同相位各点的几何位置，这些点的轨迹是一个等相位面，叫做波面(即包络面)。

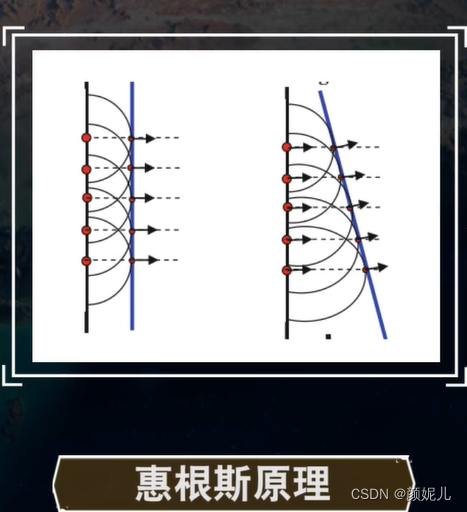
可以利用惠更斯原理证明折射波的传播路径：

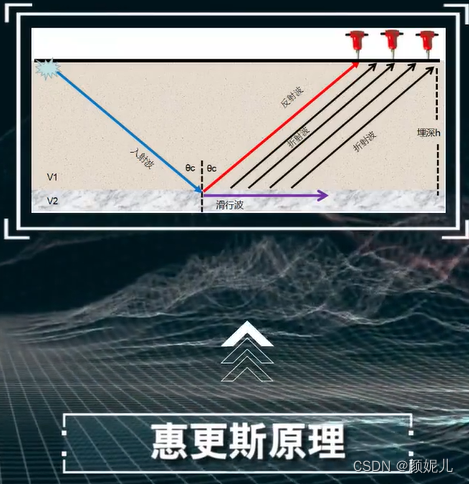
费马原理：波所走的两点之间的实际路径是传播时间最短的那一条。

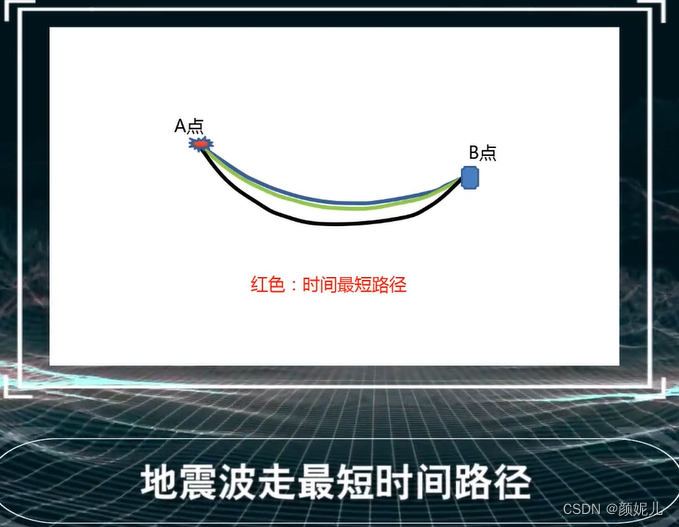
可以用费马原理证明反射定律和投射定律：

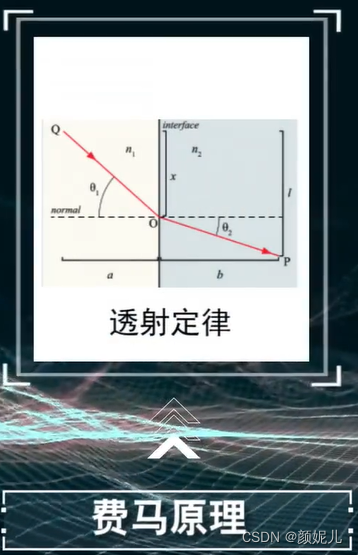
地震波的主要参数

描述地震波的主要参数：振幅、频率、相位、周期、波长、波数、时间、速度、波峰、波谷、主频、频带宽度等
振动曲线：在某一个固定的接收点，质点位移随时间变化的曲线。（在时间域里研究地震信号的特征）

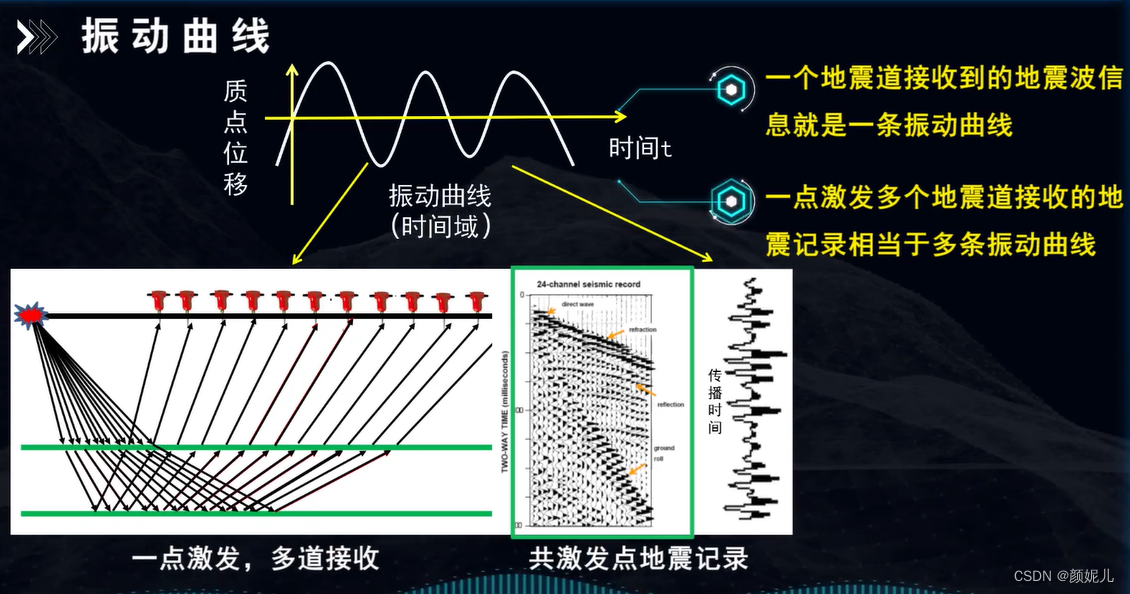
波剖面：在同一时刻质点唯一随接收点位置变化的曲线。（在空间域里研究地震信号的特征）

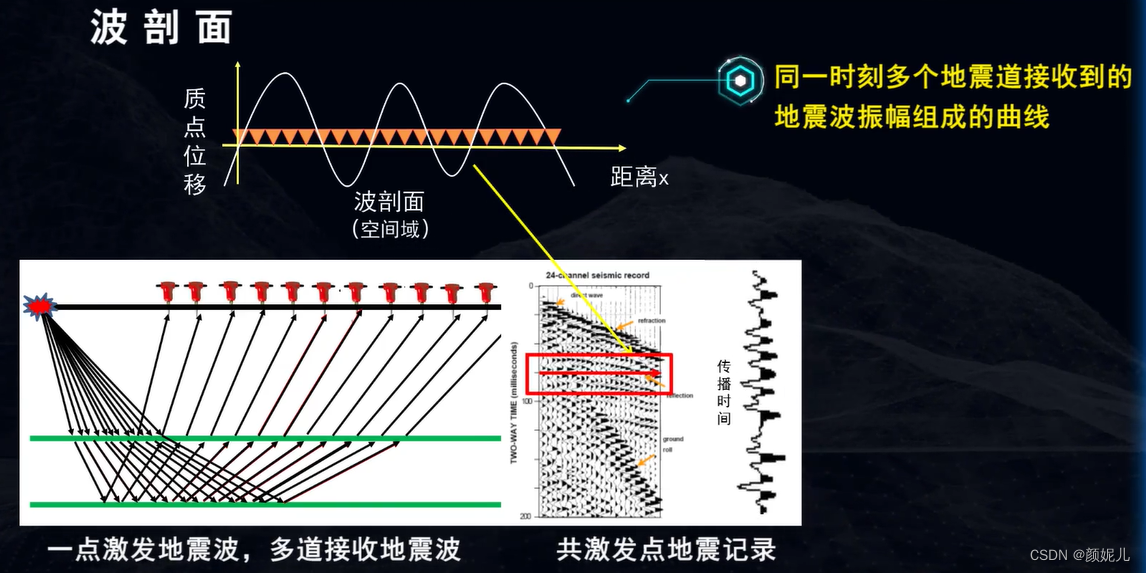
描述振动曲线的参数：

• 振幅(amplitude) A：在振动曲线上，质点唯一离开平衡位置的距离。
• 波峰和波谷：振动曲线上，正的极大值称为波峰，负的极大值称为波谷。
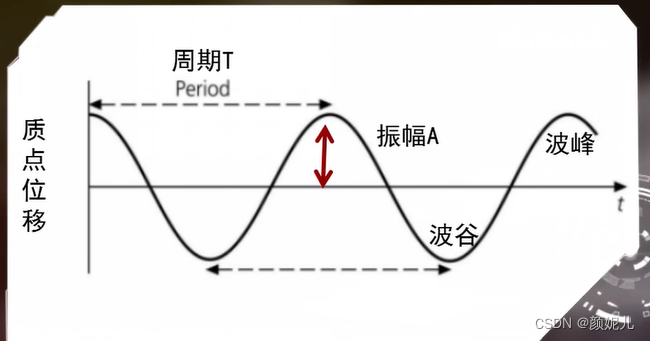
• 周期(period) $T$：在振动曲线上相邻极大值间的间隔，单位为秒或毫秒。
• 频率(frequency) $f$：单位时间内完成周期性变化的次数，是描述周期运动频繁程度的量。
• • 频率与周期互为倒数。：$T=\frac{1}{f}$或$f=\frac{1}{T}$
• 角频率 $\omega$：$\omega =2\pi f$。
• 相位(phase)：对于一个波，特定的时刻在它循环中的位置，单位是度，最大值是360度。
• 波速(velocicy) $v$：单位时间内振动所传播的距离，单位是m/s或km/s。
  
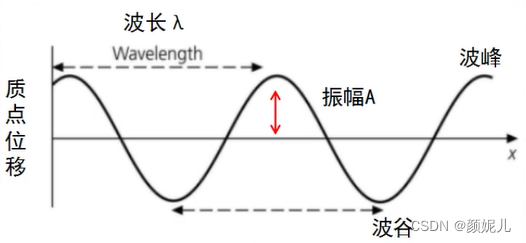
  描述波剖面的参数：
• 波长(wave lenth) $\lambda$：波在一个振动周期内传播的距离，单位是米。
• 波数(wave number) $k$：空间频率，指的是单位距离内的波长数。
• • 波长与波数互为倒数： $\lambda =\frac{1}{k}$ 或 $k=\frac{1}{\lambda }$
    
    波速$v$，频率$f$，周期$T$，波长$\lambda$，波数$k$的关系：
• $\lambda =vT=v/f$
• $v=\lambda /T=\lambda f=f/k$

像地震波这样的非周期信号，可以利用傅里叶变换提取波的频率、相位等特征参数。
傅里叶变换基本思想：几个不同振幅、相位、频率的信号叠加可以得到一个复杂的非周期信号。

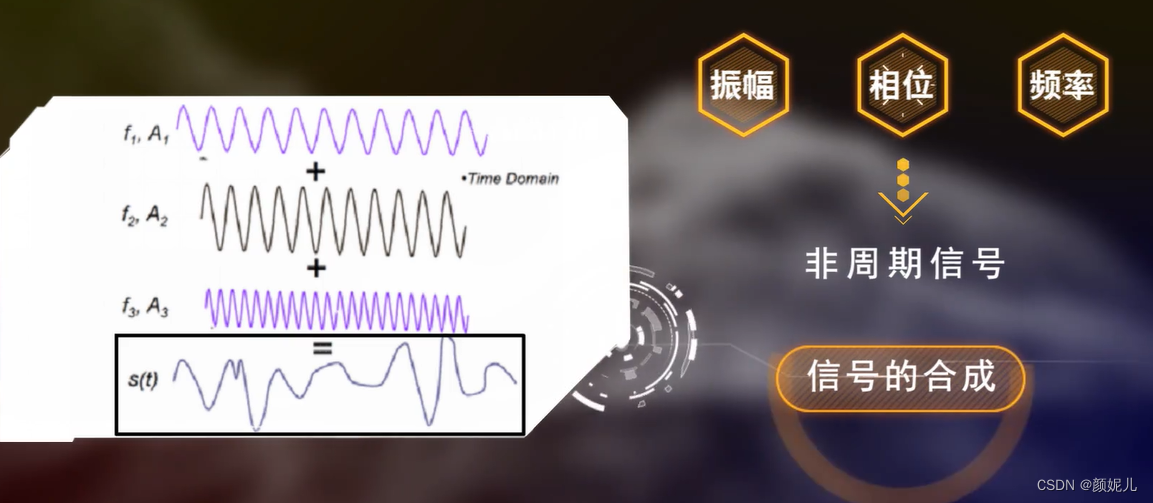
若查看非周期的复杂信号的不同频率、相位、振幅等信息组成，叫做信号的分解。
地震波的频谱的两个主要参数：

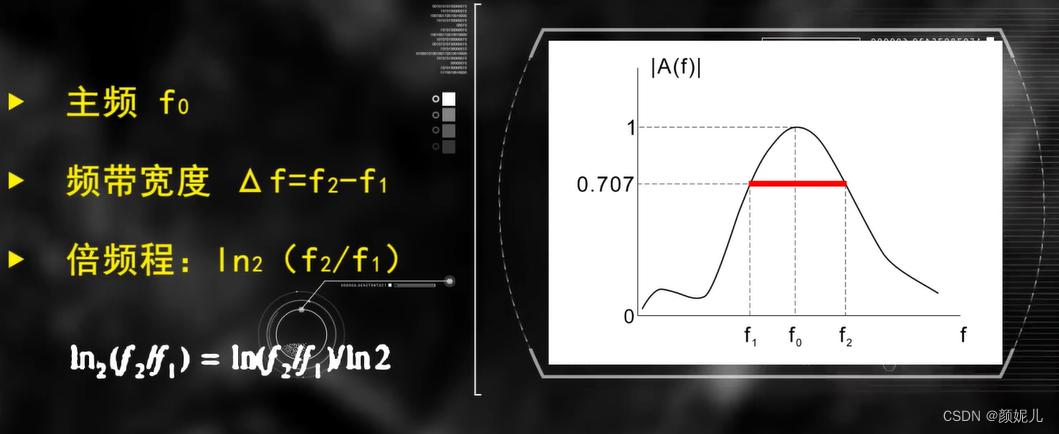
• 主频 $f_0$：频谱曲线极大值对应的频率。
• 频带宽度：频谱曲线上地震波绝大部分能量集中在那个频率范围内。
  
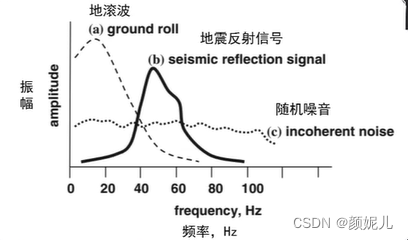
  不同地震信号的频带范围具有较大差异：
  

地震波速度

地震波速度：地震波在地下岩层中传播的距离与时间的比值，单位是m/s或km/s。地震波速度在空气中的传播速度是340m/s；近地表速度大约是数百米/秒；地震波的纵波速度在地下2885千米是达到最大，可以达到13.7km/s。
影像地震波速度的主要因素：








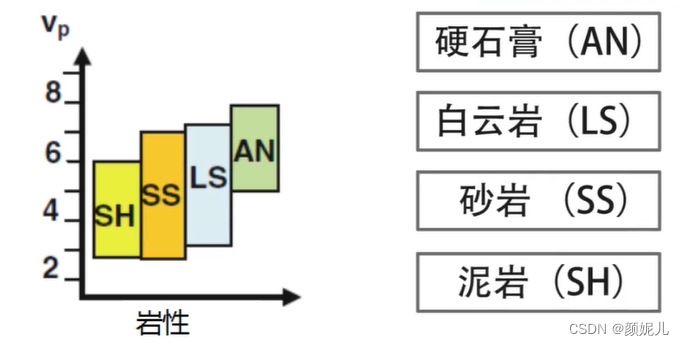
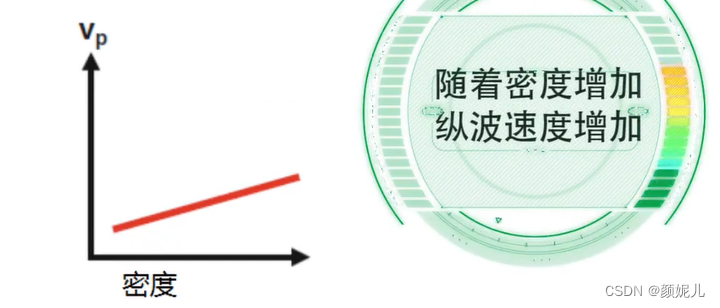
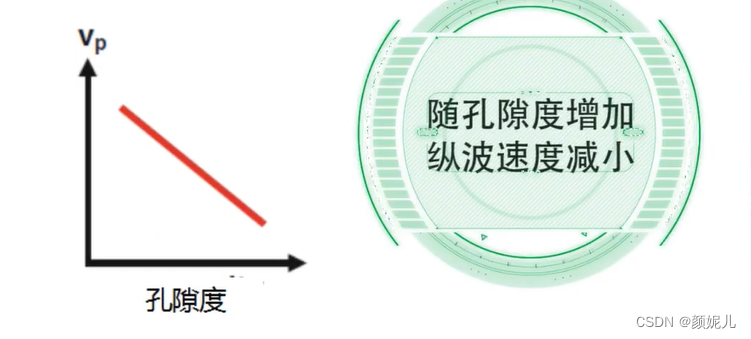
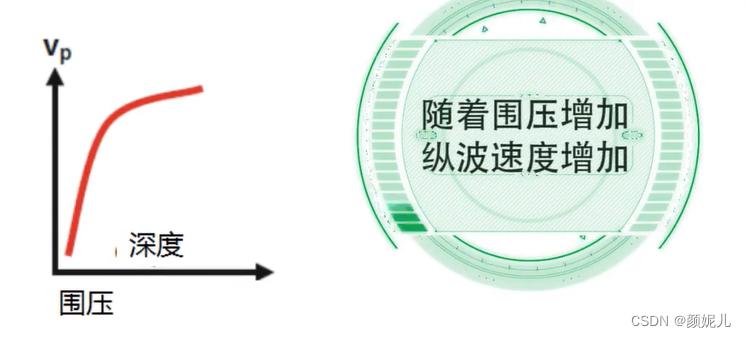
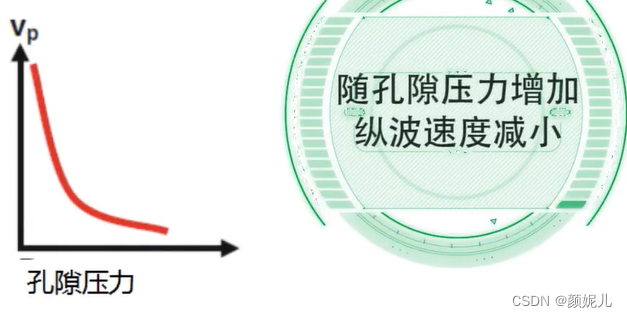
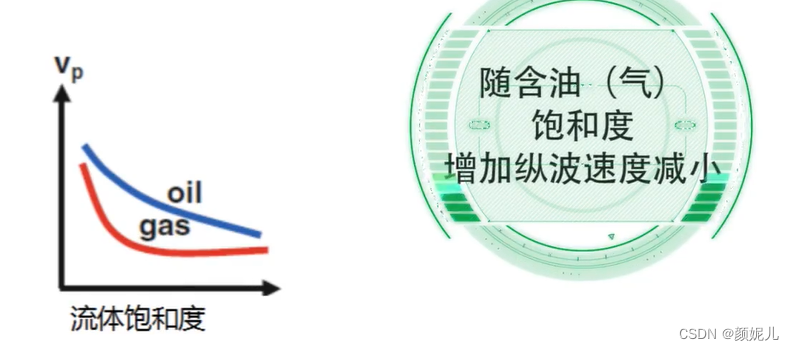
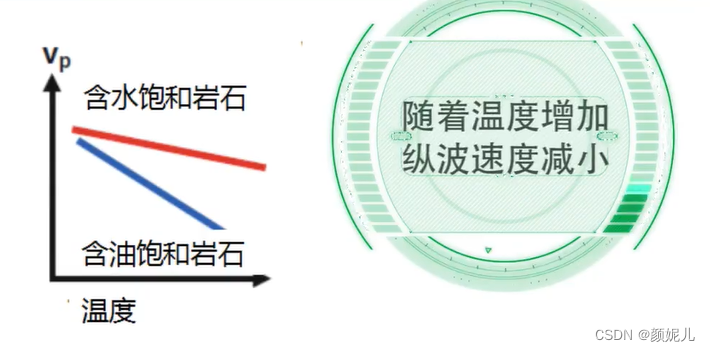
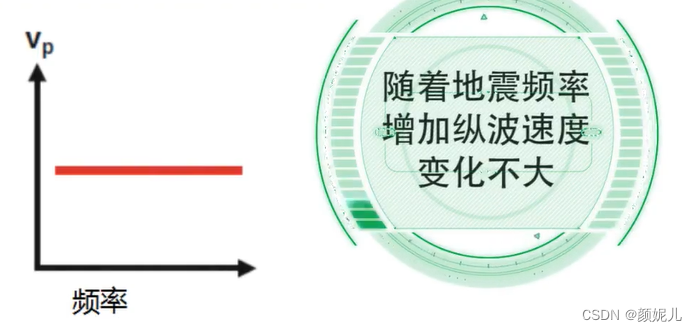
（面波的速度随频率变化而发生变化，有频散现象）
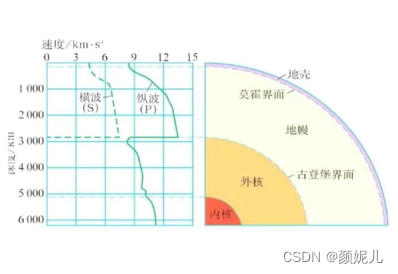
墨霍界面： 莫霍面是划分地壳与地幔的界面，位于地表以下数千米到30—40km的深度，纵波速度从7.0 km/s跳跃增加到8.1 km/s左右，横波速度从4.2 km/s增加到4.4 km/s左右。
古登堡面： 古登堡面是具有高密度的固体地幔与具有液态性质的外核之间的界面（核幔界面）。位于地下2900km深度，横波到达这一界面即告消失；纵波能够通过，但通过后其速度明显减慢。同时，纵波到达该界面还明显地发生反射与折射，出现纵波阴影带，即纵波在地表的一定区间不能被接受的地带。

地震子波 seimic wavelet

地震子波是组成地震记录的基本元素。
现代数学中，wavelet被称为子波。地震勘探会用到wavelet transformer(小波变换)这个数学工具，但是地震子波和小波没有任何关系。
地震子波的形成：炸药产生一个延续时间极短的尖脉冲，爆炸点附近的介质以冲击波的形式传播，当爆炸脉冲向外传播一定距离以后，地层产生的弹性形变再向外传播，由于介质对高频成分的吸收，波形发生明显的变化，直到传播更大的距离以后，波形逐渐稳定，形成一个具有两到三个相位、有一定延续时间的地震波，我们称这个波为地震子波。

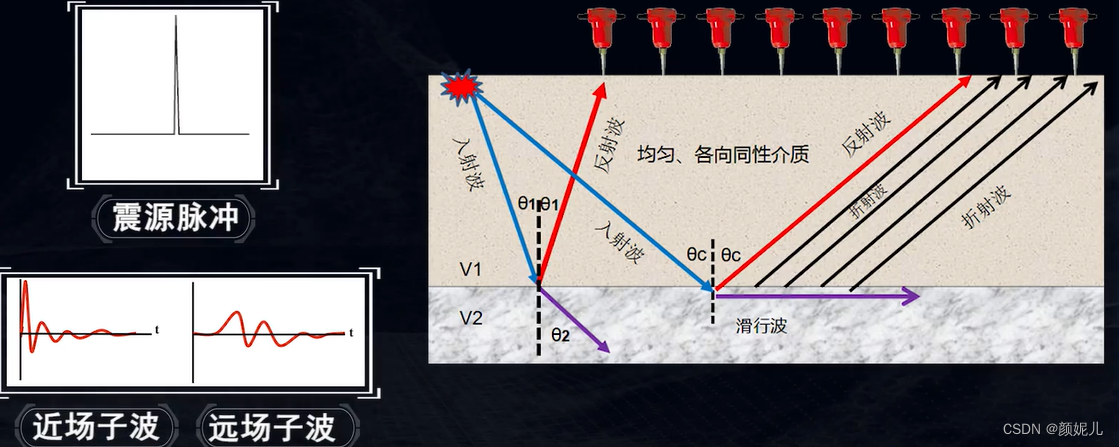
地震子波的特点：有确定的起始时间（因果性）；有限的能量；有一定延续时间的信号。


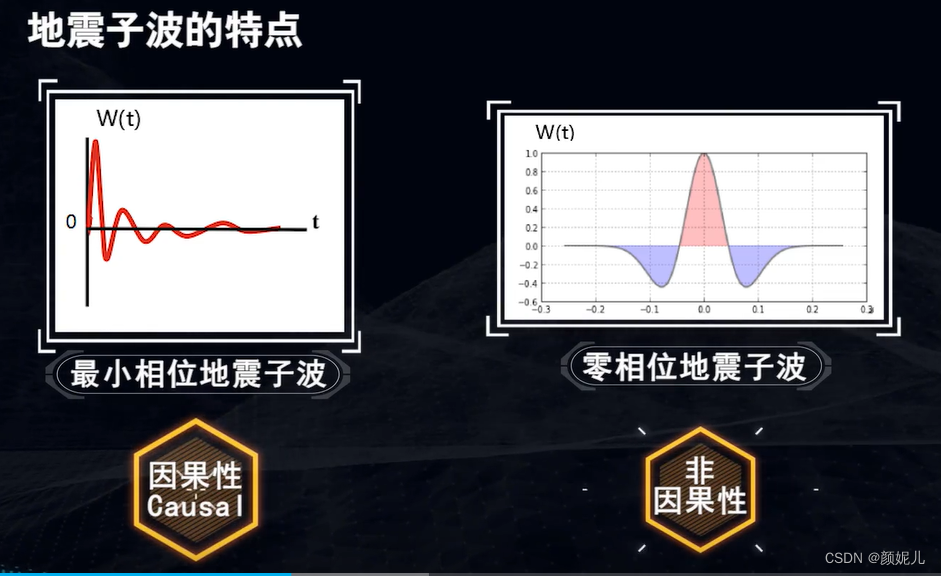
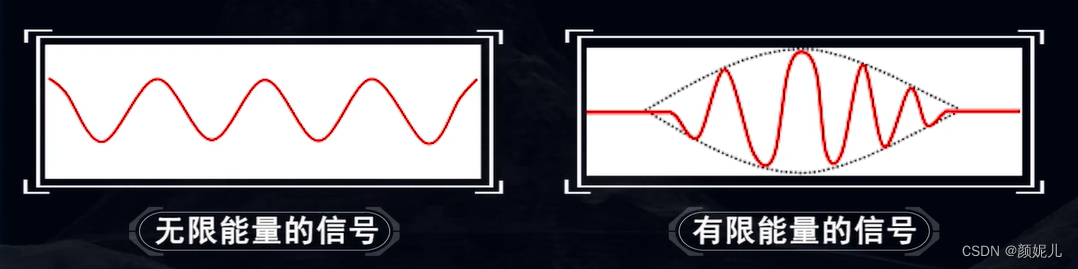
地震子波的关键属性：振幅、频率、相位
通过傅里叶变化对地震子波进行频谱分析，我们从而可以了解地震子波的频率特征和相位特征。
不同时间延续的地震子波对应的频谱中，我们可以看到子波越尖锐，则频带越宽，地震勘探分辨率也就越高，如下图所示：

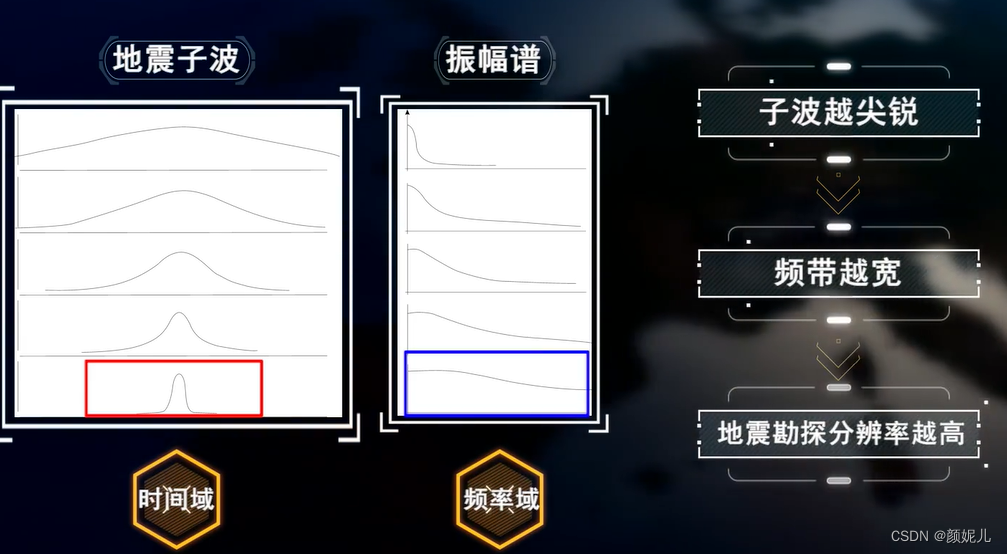
根据地震子波的相位特征的不同，可以将子波分为以下四类：

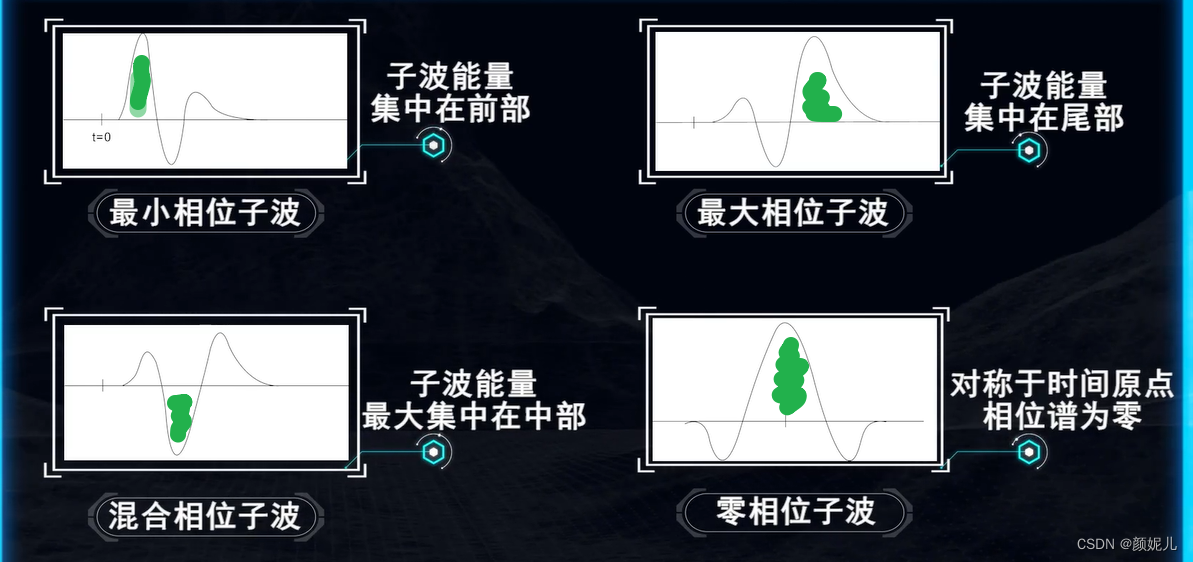
不同类型地震源激发的地震子波特征不同，如图：
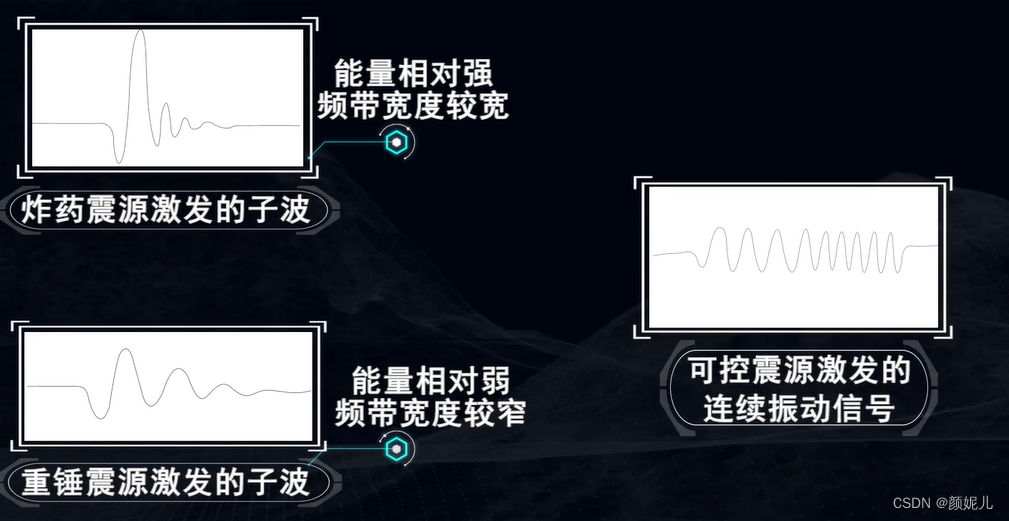理论地震子波
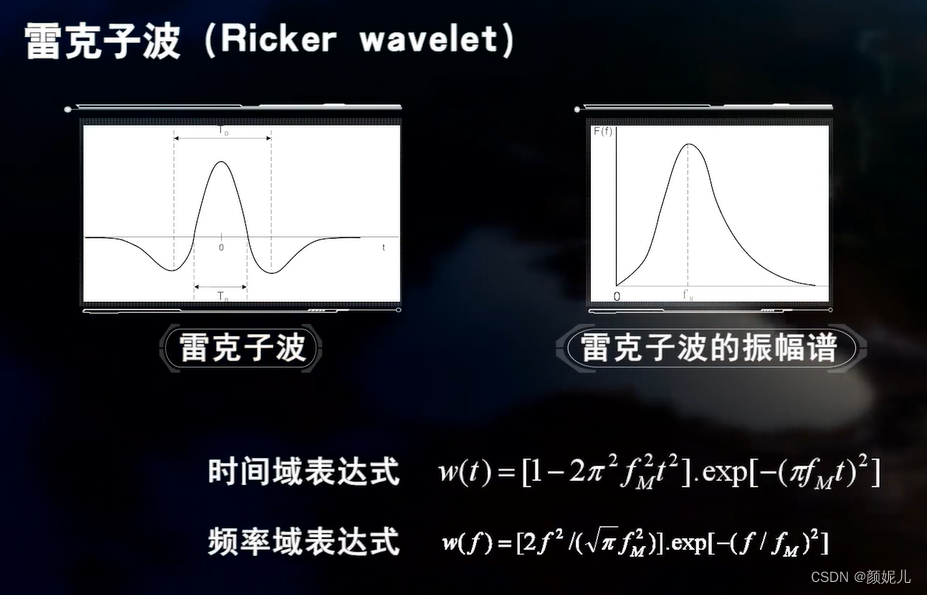
雷克子波零相位子波在地震正演模拟、合成地震记录制作、反演中常用到：

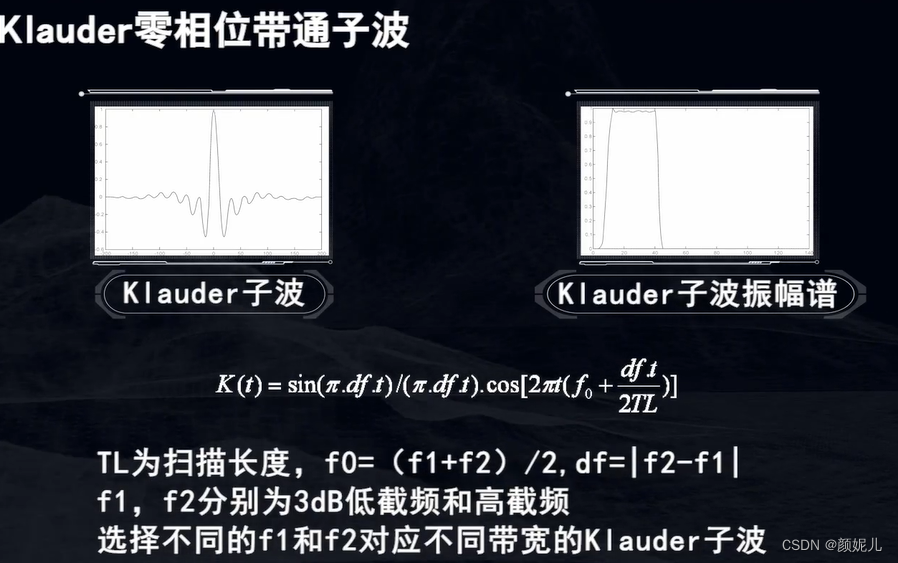
Klauder零相位子波在地震可控震源研究中适用：

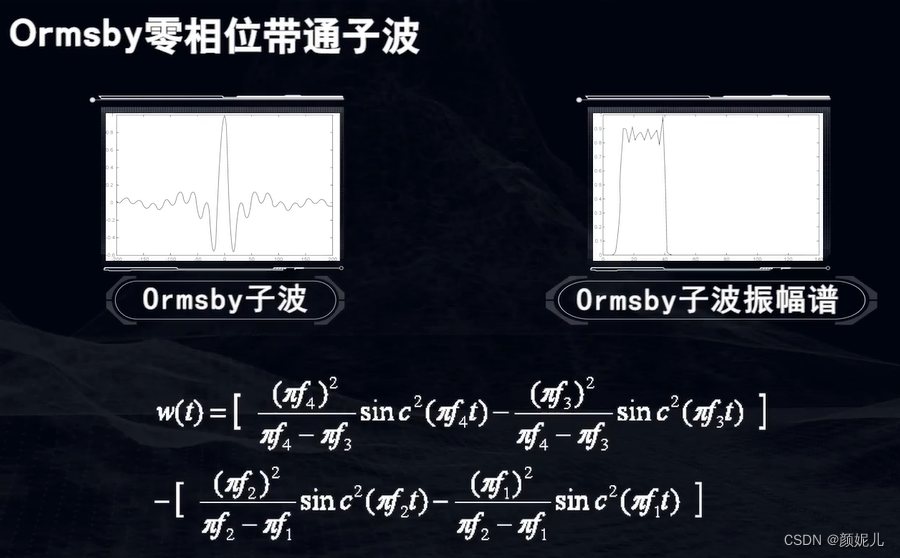
Ormsby零相位子波：

Ormsby最小相位子波：

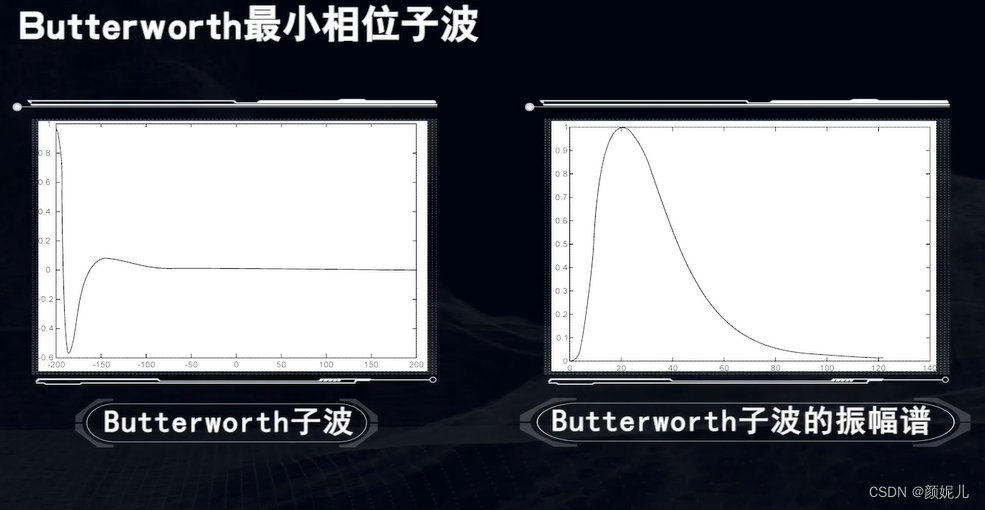
随时间发生变化的子波叫时变子波；随空间发生变化的子波叫空变子波。
地震子波的极性：

地震子波的作用：

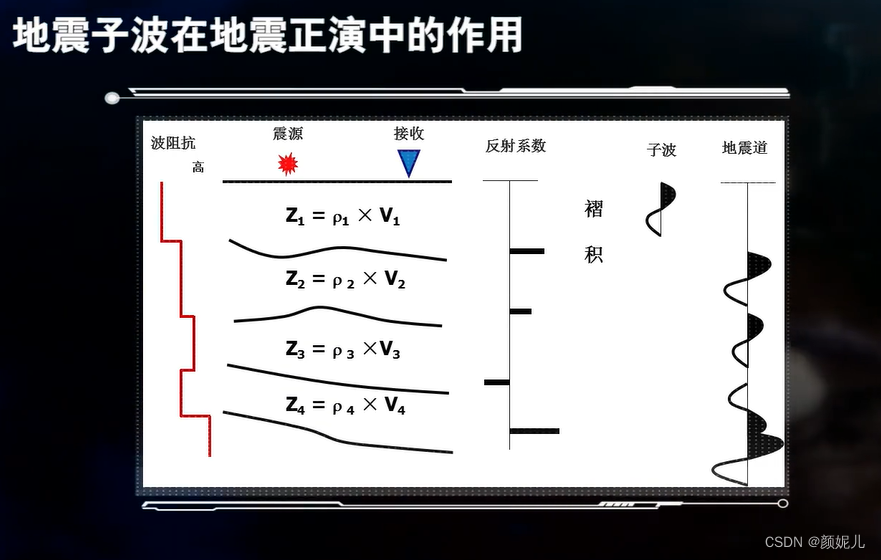
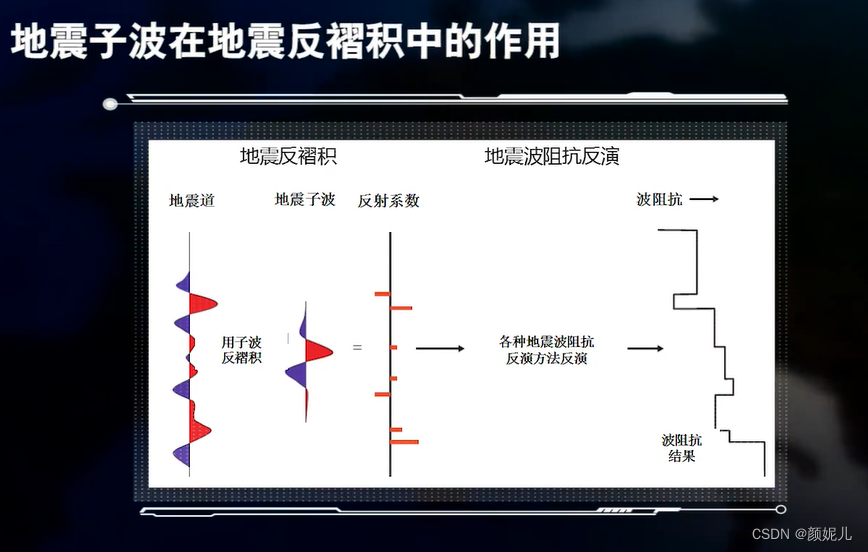
地震合成记录

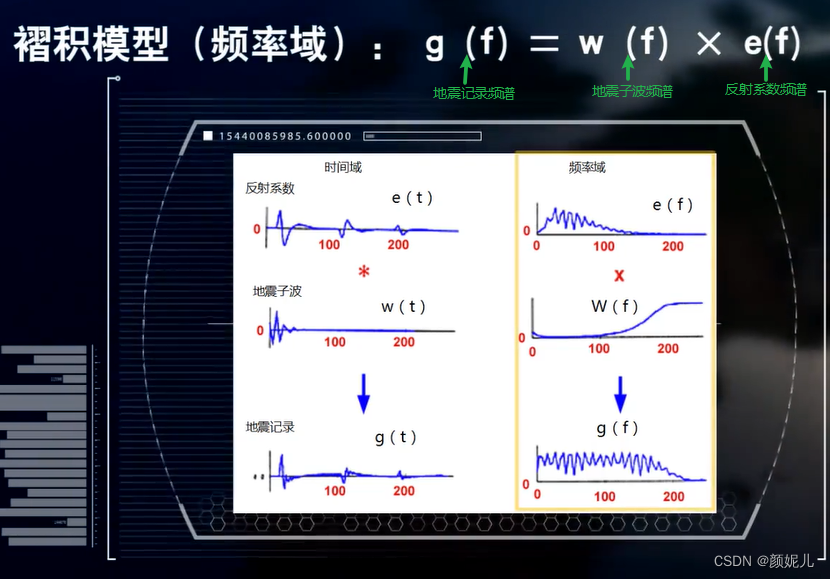
相关介绍：地震褶积模型：

反射褶积模型认为——地震记录$g(t)$是真元地震子波$w(t)$和地下地层反射系数$e(t)$褶积的结果：

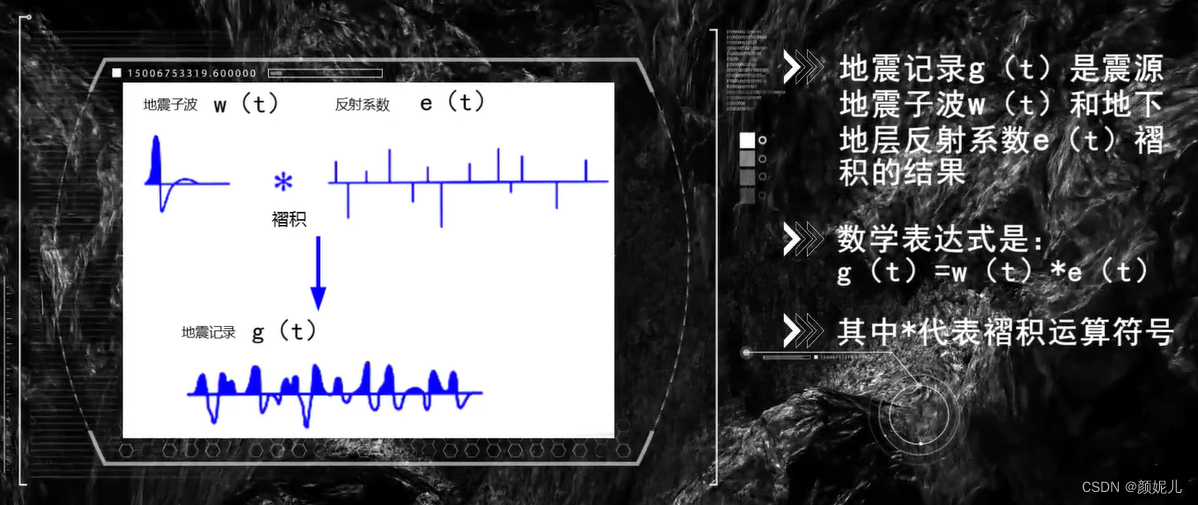
褶积模型的离散形式：
$$g_k=\sum _{i=0}^m{e}_i{w}_{k-i}$$

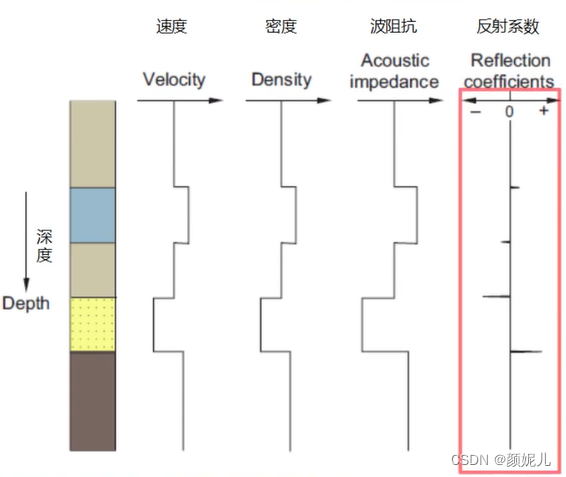
制作合成地震记录：对某一口井进行声波测井、密度测井，可以得到声波测井曲线和密度测井曲线，将速度和密度对应相乘，得到波阻抗曲线，然后根据地震垂直反射系数方程计算反射系数序列；给定一个震源子波，地震记录上看到的反射波波形就是地震子波在地下各反射截面上发生时反射形成的。


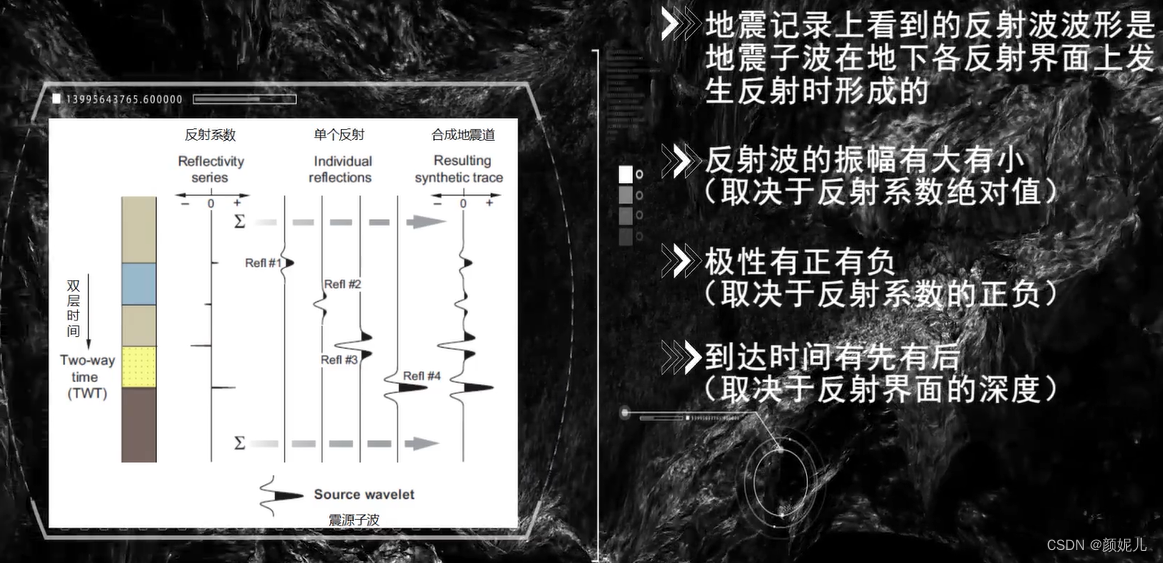
不同频率的地震子波与反射系数褶积，得到的合成地震记录是有差异的——地震子波主频越高，地震纵向分辨率越高。如下图所示：


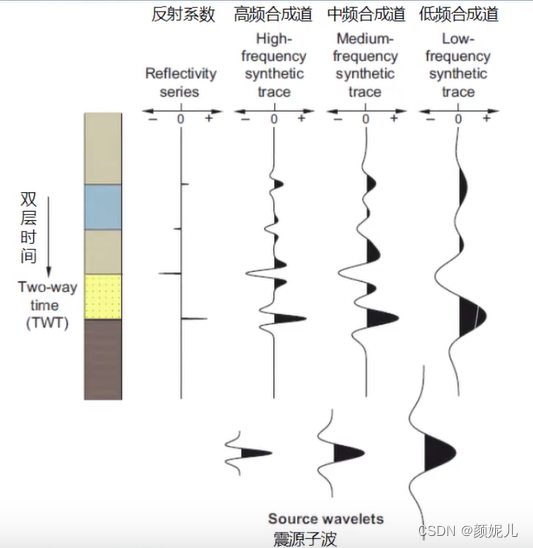
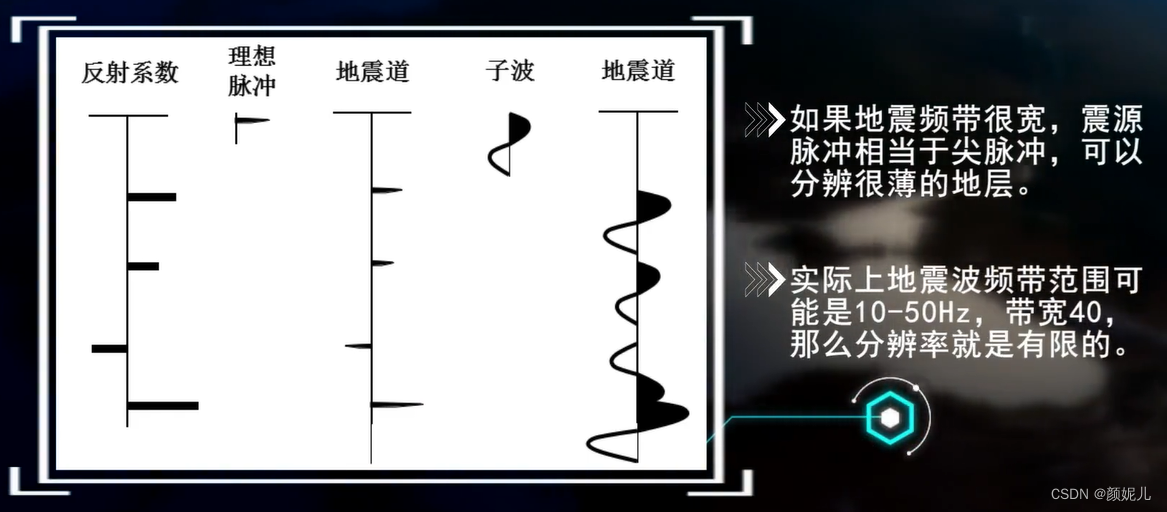
实际的地震记录是地震子波、反射系数以及各种影像因素共同褶积的结果：

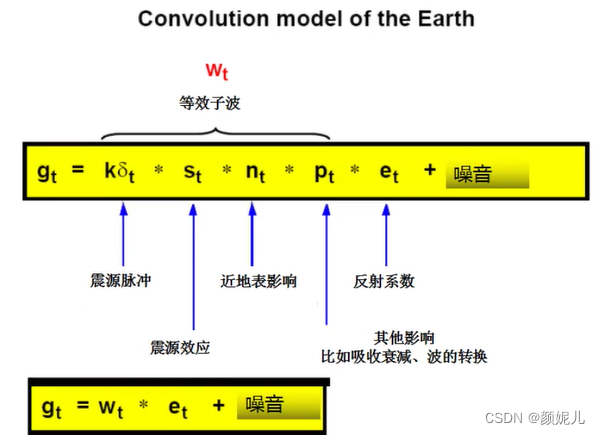
人工合成地震记录制作中，井的纵坐标是深度，合成记录的纵坐标是时间，所以我们要用合适的平均速度进行时深转换：

地震合成记录可以对层位进行准确的标定：

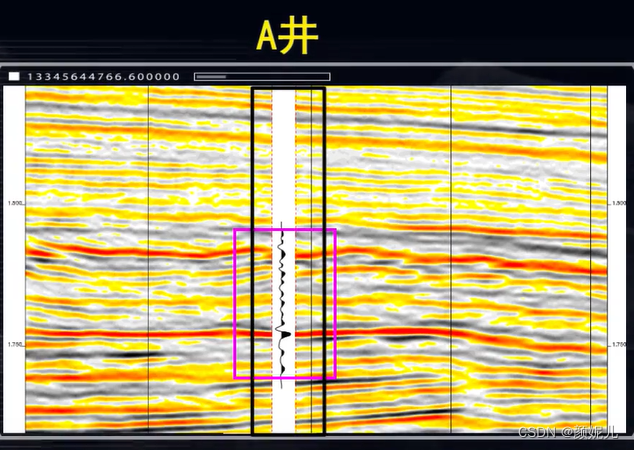
地震反演与地震正演：