本文主要是介绍加法秘密共享比较-PPA,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
概要:加法秘密共享的比较可以简化为MSB提取操作,即
a < b = MSB ( a − b ) . a<b = \textbf{MSB}(a-b). a<b=MSB(a−b).
值得注意的是,MSB是二元秘密共享, a a a和 b b b是环上的秘密共享。需要 B2A \textbf{B2A} B2A转换。
1. 空间编码
为了表达有符号整数,把环分成两半,其中下半环 [ 0 , 2 l − 1 − 1 ] [0,2^{l-1}−1] [0,2l−1−1]表示非负值和上半环 [ 2 l − 1 [2^{l-1} [2l−1, 2 l − 1 ] 2^{l}−1] 2l−1]表示负值。
2. 基础知识
2.1. 加法器
考虑1比特的加法器:输入有三个: A A A, B B B 和 C C C。其中, A A A 和 B B B 代表输入, C C C 表示低位的进位。输出中, X = A ⊕ B ⊕ C X=A\oplus B\oplus C X=A⊕B⊕C 表示本位置的结果, Y = A ⋅ B ⊕ C ⋅ ( A ⊕ B ) Y=A\cdot B\oplus C\cdot(A\oplus B) Y=A⋅B⊕C⋅(A⊕B) 表示对高位的进位。真值表:
| A | B | C | X | Y |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
可以看到,在求解高位进位 Y Y Y时,当 A A A 和 B B B为 00 00 00或者 11 11 11低进位不起作用,只有当 A A A 和 B B B互补时需要低进位参与。
因而,在计算两个 l l l 比特的份额 e e e 和 f f f 的时候,可以定义:
p i = e i ⊕ f i , g i = e i ⋅ f i p_i=e_i\oplus f_i,g_i=e_i\cdot f_i pi=ei⊕fi,gi=ei⋅fi
其中, p i p_i pi被称为 propagate bit, g i g_i gi被称为 generate bit。可得(与真值表一致):
c i = g i ⊕ ( p i ⋅ c i − 1 ) = e i ⋅ f i ⊕ c i − 1 ⋅ ( e i ⊕ f i ) c_{i}=g_i\oplus (p_i\cdot c_{i-1})=e_i\cdot f_i\oplus c_{i-1}\cdot(e_i\oplus f_i) ci=gi⊕(pi⋅ci−1)=ei⋅fi⊕ci−1⋅(ei⊕fi)
因而:
c 0 = g 0 c 1 = g 1 ⊕ ( p 1 ⋅ g 0 ) c 2 = g 2 ⊕ ( p 2 ⋅ g 1 ) ⊕ ( p 2 ⋅ p 1 ⋅ g 0 ) ⋮ c l − 1 = g l − 1 ⊕ ( p l − 1 ⋅ g l − 2 ) ⊕ ⋯ ⊕ ( p l − 1 ⋯ p 1 ⋅ g 0 ) c_0=g_0\\ c_1=g_1\oplus (p_1\cdot g_0)\\ c_2=g_2\oplus (p_2\cdot g_1)\oplus (p_2\cdot p_1\cdot g_0)\\ \vdots\\ c_{l-1}=g_{l-1}\oplus (p_{l-1}\cdot g_{l-2})\oplus\cdots\oplus(p_{l-1}\cdots p_1\cdot g_0) c0=g0c1=g1⊕(p1⋅g0)c2=g2⊕(p2⋅g1)⊕(p2⋅p1⋅g0)⋮cl−1=gl−1⊕(pl−1⋅gl−2)⊕⋯⊕(pl−1⋯p1⋅g0)
2.2. PPA
为了减少与门的深度,PPA在计算 c i c_i ci时进行了并行优化,即利用分层的思路,每层进行一些 p i p_i pi和 g i g_i gi的合并减少总计算。
g o = g i 2 ⊕ ( p i 2 ⋅ g i 1 ) , p o = p i 2 ⋅ p i 1 g_o=g_{i_2}\oplus (p_{i_2}\cdot g_{i_1}),p_o=p_{i_2}\cdot p_{i_1} go=gi2⊕(pi2⋅gi1),po=pi2⋅pi1
而目前的多种PPA变体,其主要设计思路是在加法器范围、电路深度、节点输出数量和整体布线四点上做出均衡。
常见的Sklansky变体,利用二分法进行求解。
即:
- 计算两两相邻比特 i i i和 i + 1 i+1 i+1之间的合并
- 计算数量减半,重复第一步。
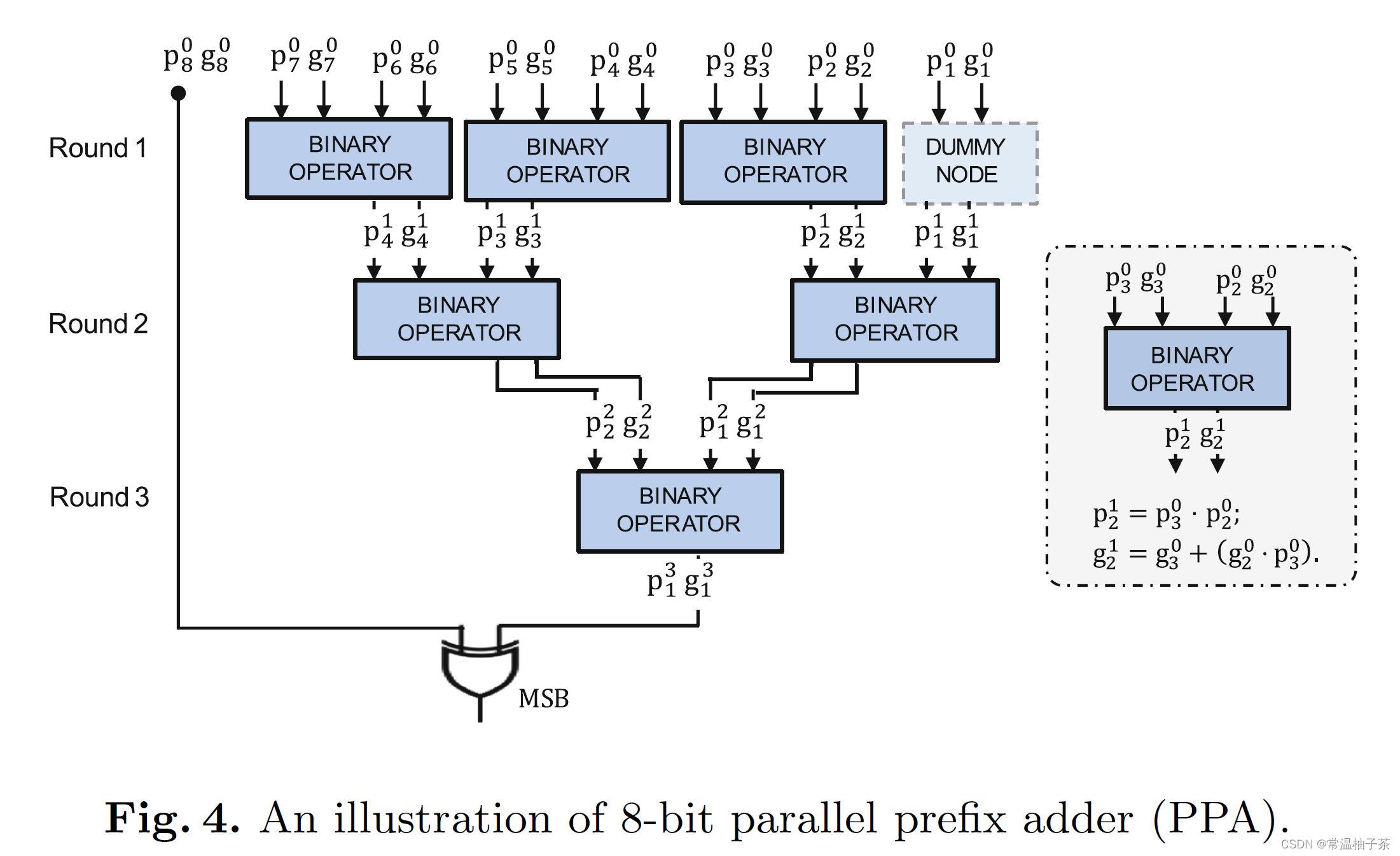
2.3. MSB
提取秘密共享份额的最高有效位。
- 将份额本地分解为比特
- 计算PPA公式
- 并行分层聚合
- 求解最高有效位 c l − 1 c_{l-1} cl−1

3. 比较
本地计算 a − b a-b a−b 的份额,通过PPA算法 MSB ( a − b ) \textbf{MSB}(a-b) MSB(a−b)求解其最高有效位 c l − 1 c_{l-1} cl−1,由于明文空间编码,当 c l − 1 = 1 c_{l-1}=1 cl−1=1时负数空间, a < b a<b a<b;否则正数空间, a ≥ b a\ge b a≥b。
图片来源:
X. Liu, Y. Zheng, X. Yuan, and X. Yi, “Medisc: Towards secure and lightweight deep learning as a medical diagnostic service,” in Proc. of ESORICS, 2021
.
这篇关于加法秘密共享比较-PPA的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



