本文主要是介绍【JZOJ4638】第三条跑道,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Description
Solution
这题码农,表示又被出题人虐了。
我们发现 ai 以及 x 都小于等于600,于是我们可以分解质因数,我们看看部分质数表:
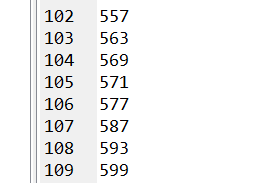
这说明600以内的指数只有109个(那么这里有只HowarLi翻车了)。
于是我们用线段树,对于每个区间记录109个质数被该区间多少个数包含。
由于要区间修改,我们再记录109个
那么,现在我们知道 φ(n)=n∏mi=1(1−1pi) ( pi 表示的 n 质因数,
观察上面的式子,一个很显然的结论是 φ(pn)=pφ(n)(p|n) (这里 p 是质因数)
那如果
那么
那么至于区间乘上一个数 x ,先给它分解质因数,得出
对于一个质因数 xi ,我们已知该区间有 Axi 个数包含它,那么它们对欧拉积的贡献为: xAxii 。
但是,没有包含的怎么办?由上可得,没有包含的将乘上一个 (xi−1) ,所以该区间没有被包含的对欧拉积的贡献就为: (xi−1)r−l+1−Axi 。
最后给修改的区间打上 lazy 标记即可。
但是,怎样下传标记?
我们对于一个区间有 lazyi 表示第 i 个质数还要下传多少次。那么,我们先给这个区间下传一次,具体下传请看上述修改部分。然后,由于还要下传
对于查询,直接找到区间欧拉积即可。
时间复杂度:
然而,这题看似容易,实际上打对调对需要花费大量时间。
可以打一个线性筛法求 φ <script type="math/tex" id="MathJax-Element-29">φ</script>来方便调试。
Code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#define fo(i,j,k) for(int i=j;i<=k;i++)
#define fd(i,j,k) for(int i=j;i>=k;i--)
#define N 10010
#define M 601
#define mo 100000007
#define ll long long
using namespace std;
int pr[M],cnt=0,phi[M];
int a[N];
bool bz[M];
struct node{int a[120];int lz[120];ll s;
}tr[N*4];
int ph[N],s1[N],s2[N];
int ls[120];
int map[M];
ll pow(ll m,int n)
{ll b=1;while(n){if(n%2==1) b=b*m%mo;n/=2;m=m*m%mo;}return b;
}
void pre()
{int cnt=0;for(int i=2;i<M;i++){if(!bz[i]) pr[++cnt]=i,map[i]=cnt,phi[i]=i-1;for(int j=1;j<=cnt && i*pr[j]<M;j++){bz[i*pr[j]]=true; if(i%pr[j]==0){phi[i*pr[j]]=phi[i]*pr[j];break;}else phi[i*pr[j]]=phi[i]*(pr[j]-1);}}
}
void get(int v,int x)
{int z=0,t=x;while(x){z++;if(pr[z]*pr[z]>t) break;if(x%pr[z]==0){tr[v].a[map[pr[z]]]=1;while(x%pr[z]==0) x/=pr[z];}}if(x>1) tr[v].a[map[x]]=1;
}
void getlazy(int v,int x)
{int z=0,t=x;while(x){z++;if(pr[z]*pr[z]>t) break;if(x%pr[z]==0){while(x%pr[z]==0) tr[v].lz[map[pr[z]]]++,ls[map[pr[z]]]++,x/=pr[z];}}if(x>1) tr[v].lz[map[x]]++,ls[map[x]]++;
}
void put(int v,int l,int r)
{int mid=(l+r)/2;fo(i,1,109){if(!tr[v].lz[i]) continue;tr[v*2].s=tr[v*2].s*pow(pr[i],tr[v*2].a[i])%mo*pow(pr[i]-1,mid-l+1-tr[v*2].a[i])%mo;tr[v*2+1].s=tr[v*2+1].s*pow(pr[i],tr[v*2+1].a[i])%mo*pow(pr[i]-1,r-mid-tr[v*2+1].a[i])%mo;tr[v*2].a[i]=mid-l+1;tr[v*2+1].a[i]=r-mid;tr[v*2].s=tr[v*2].s*pow(pow(pr[i],mid-l+1),tr[v].lz[i]-1)%mo;tr[v*2+1].s=tr[v*2+1].s*pow(pow(pr[i],r-mid),tr[v].lz[i]-1)%mo;tr[v*2].lz[i]+=tr[v].lz[i];tr[v*2+1].lz[i]+=tr[v].lz[i];tr[v].lz[i]=0;}
}
void build(int v,int l,int r)
{if(l==r){get(v,a[l]);tr[v].s=phi[a[l]];return;}int mid=(l+r)/2;build(v*2,l,mid);build(v*2+1,mid+1,r);fo(i,1,109)tr[v].a[i]=tr[v*2].a[i]+tr[v*2+1].a[i];tr[v].s=tr[v*2].s*tr[v*2+1].s%mo;
}
void change(int v,int l,int r,int x,int y,int p)
{if(l==x && r==y){getlazy(v,p);fo(i,1,109)if(ls[i]){tr[v].s=tr[v].s*pow(pr[i],tr[v].a[i])%mo*pow(pr[i]-1,r-l+1-tr[v].a[i])%mo;tr[v].a[i]=r-l+1;tr[v].s=tr[v].s*pow(pow(pr[i],r-l+1),ls[i]-1)%mo;ls[i]=0;}return;}put(v,l,r);int mid=(l+r)/2;if(y<=mid) change(v*2,l,mid,x,y,p);else if(x>mid) change(v*2+1,mid+1,r,x,y,p);else{change(v*2,l,mid,x,mid,p);change(v*2+1,mid+1,r,mid+1,y,p);}fo(i,1,109)tr[v].a[i]=tr[v*2].a[i]+tr[v*2+1].a[i];tr[v].s=tr[v*2].s*tr[v*2+1].s%mo;
}
ll ans=1;
void find(int v,int l,int r,int x,int y)
{if(l==x && r==y){ans=ans*tr[v].s%mo;return;}int mid=(l+r)/2;put(v,l,r);if(y<=mid) find(v*2,l,mid,x,y);else if(x>mid) find(v*2+1,mid+1,r,x,y);else{find(v*2,l,mid,x,mid);find(v*2+1,mid+1,r,mid+1,y);}
}
int main()
{freopen("2.in","r",stdin);freopen("2.out","w",stdout);pre();phi[1]=1;int n,T;cin>>n;fo(i,1,n) scanf("%d",&a[i]);build(1,1,n);cin>>T;while(T--){int z,l,r;scanf("%d %d %d",&z,&l,&r);if(!z){int x;scanf("%d",&x);change(1,1,n,l,r,x);}else{ans=1;find(1,1,n,l,r);printf("%lld\n",ans);}}
}这篇关于【JZOJ4638】第三条跑道的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!