D. Andrey and Escape from Capygrad Round 892 (Div. 2) 1859D

Problem - D - Codeforces

题目大意：在一个从0到1e9的数轴上，有n个传送门，每个传送门有4个参数，l,r,a,b，可以从[l,r]之间的任意内进入传送门，并传送到[a,b]之间的任意位置，[l,r]一定包含[a,b]，有q个起始位置，问从每个位置出发能到达的最远位置是哪

1<=n<=2e5；1<=l<=a<=b<=r<=1e9；1<=q<=2e5

思路：因为我们要走到最远的位置，所以如果我们在某一个传送门的[b,r]范围内，那么我们肯定不会用这个传送门，在原地不动就是最远位置，如果我们要用这个传送门，我们也肯定只会传送到b的位置，即这个传送门能到达的最远位置，所以其实对于某一个传送门，我们只要在[l,b]的范围内，就能到达b，r和a其实是无关项。

这样的话每个传送门就变成了一个很普通的[l,r]区间，r即为原来的b，因为我们可以无限利用传送门，所以相交的传送门可以合并

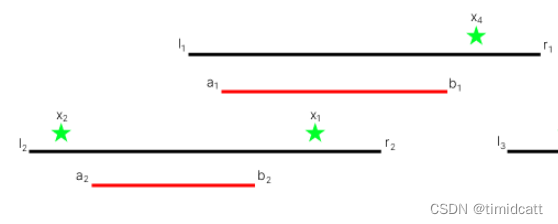
 例如上图这两个传送门，[l2,b2]、[l1,b1]，因为我们只要能进其中一个传送门，就一定能进另一个，所以我们只要在[l2,b1]的范围内，就可以到达b1的位置，也就是这两个区间合并成了[l2,b1]这样一个新区间。

我们将所区间都合并完成后，任意两个区间都没有重合，这样对于每个起始位置，我门就可以用二分找到他属于哪个区间，他能到达的最远位置也就是区间的右端点，如果不在任何区间内，原地不动就是最远

//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 5;
const int INF = 0x7fffffff;
const int MOD = 998244353;
int n;
pair<int, int>p[N];
void solve()
{cin >> n;init();for (int i = 1; i <= n; i++){int a, b, c, d;cin >> a >> b >> c >> d;p[i] = { a,d } ;}sort(p + 1, p + n + 1);//将所有原区间按从小到大排序int ma = 0;vector<pair<int, int>>por;for (int i = 1; i <= n; i++){		if (p[i].first > ma){//当前区间的左端点超过了当前记录的最远位置por.push_back(p[i]);//记录新区间ma = max(ma, p[i].second);}else{//当前区间和之前记录的区间有重合if (p[i].second <= ma)continue;//被包含的直接不管pair<int, int>temp = por.back();por.pop_back();por.push_back({ temp.first,p[i].second });//合并这两个区间ma=p[i].second;}}int q;cin >> q;for (int i = 1; i <= q; i++){int x;cin >> x;int l = 0, r = por.size() - 1, mid;int ans = x;//最远距离初始化为当前位置while (l <= r){//二分查找当前位置在哪个区间mid = (l + r) >> 1;int nl = por[mid].first;int nr = por[mid].second;if (nr >= x && nl <= x){ans = por[mid].second;break;}if (nr < x){l = mid + 1;}else if (nl > x){r = mid - 1;}}cout << ans << " ";}cout << endl;return;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin >> t;while (t--){solve();}
}