计算机组成原理学习总结2 运算方法和运算器

第二章 运算方法和运算器

2.0 数据的类型
2.1 数据与文字的表示方法
2.2 定点加法、减法运算
2.3 定点乘法运算
2.4 定点除法运算
2.5 定点运算器的组成
2.6 浮点运算方法和浮点运算器

2.0 数据的类型

按数制分：
十进制：在微机中直接运算困难；
二进制：占存储空间少，硬件上易于实现，易于运算；
十六进制：方便观察和使用；
按数据格式分：
真值：没有经过编码的直观数据表示方式；
带正负号的数据，任何数制均可；
机器数：符号化后的数值表示；
符号也被编码，不能随便忽略任何位置上的0或1 ；
位数固定，一般为字节整倍数，如8位、16位、32位……；
可用原码、反码、补码、移码等形式编码；

按数据的表示范围分：
定点数
小数点位置固定，数据表示范围小；
浮点数
小数点位置不固定，数据表示范围较大。
按能否表示负数分：
无符号数
数据所有位均为表示数值，只能表示正数；
有符号数
有正负之分，最高位为符号位，其余位表示数值。

2.1 数据与文字的表示方法

定点数：小数点固定在某一位置的数据；
纯小数：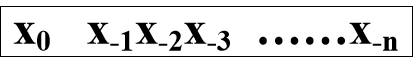
表示形式
有符号数 x=xSx-1x-2…x-n |x|≤1-2-n ;xs为符号位
无符号数 x=x0x-1x-2…x-n 0≤x ≤1-2-n ;x0=0
数据表示范围 0.0…0= 0 ≤|x|≤ 1-2-n = 0.1…1

纯整数：

表示形式
有符号数 x=xs x n-1 … x 1 x 0 |x|≤2n-1 ;xs为符号位
无符号数 x=xn x n-1 … x 1 x 0 0≤x≤2n+1-1 ;xn为数值位
注意：小数点的位置是机器约定好的，并没有实际的保存。

进制转换：

定点机的特点：
所能表示的数据范围小
数据精度较低
存储单元利用率低

数的机器码表示：

真值：正、负号加某进制数绝对值的形式称为真值，即数的 实际值，如+3，-5等
机器数：真值按某种编码方式进行编码后的数值 如：X=01011 Y=11011
即真值在机器中的表示，称为机器数，一般可以分为无符号数和有符号数两种

原码表示法：

0有两种表示法
[+0]原 = 0000 ; [-0]原 = 1000
数据表示范围
定点小数：-1<X<1
定点整数: -2n<X<2n （若数值位n=3，即：-8<X<8）
优点
与真值对应关系简单；
缺点
参与运算复杂，需要将数值位与符号位分开考虑。

模的概念

计算机中运算器、寄存器、计数器都有一定的位数，不可能容纳无限大的任意数。当运算结果超出实际的最大表示范围，就会发生溢出，此时所产生的溢出量就是模（module）。
可以把模定义为一个计量器的容量。如：一个4位的计数器，它的计数值为0～15。当计数器计满15之后再加1，这个计数器就发生溢出，其溢出量为16，也就是模等于16。
定点小数的溢出量为2，即以2为模；
• 一个字长为n+1位的定点整数的溢出量为2n+1，即
以2n+1为模。
进一步结论：
在计算机中，机器能表示的数据位数是固定的，其运算都是有模运算。
若是n+1位整数，则其模为2n+1；
若是小数，则其模为2。
若运算结果超出了计算机所能表示的数值范围，则只保留它的小于模的低n+1位的数值，超过n+1位的高位部分就自动舍弃了。

补码的定义:
任意一个数X的补码记为[x]补，
[x]补= X + M （Mod M）
当X>0时 X + M >M 自动丢失，
[x]补= X （Mod M）
当X<0时 X + M = M - | X | < M，
[x]补= X + M （Mod M）

补码表示法

特殊数据的表示
0的唯一编码： [-0]补＝ [24+(-0)] mod 24＝0000＝[+0]补
原码中用于表示-0的编码10…0，补码中表示负的最小值；
数据表示范围
定点小数：-1≤X<1
定点整数: -2n≤X<2n （若数值位n=3，则-8≤X<8）
加减运算规则
只要结果不溢出，可将补码符号位与数值位一起参与运算。
[[x]补]补＝[x]原

由原码求补码的简便原则(负数)
除符号位以外,其余各位按位取反，末位加1；
除符号位以外,从最低位开始，遇到的第一个1以前的各位保持不变，之后各位取反。

求相反数的补码
由[X]补求[-X]补
连同符号位的所有位一起取反，末位加1；
例：X= -0.010 1011
[X]补=1.101 0101 ；[ - X]补=0.010 1011 ；

由[-X]补求[X]补，此规则同样适用

移码表示法
移码通常用于表示浮点数的阶码
用定点整数形式的移码
定义： [x]移=2n+x 2n > x ≥ -2n
与[x]补的区别：符号位相反
优点：
可以比较直观地判断两个数据的大小；
浮点数运算时，容易进行对阶操作；
表示浮点数阶码时，容易判断是否下溢；
当阶码为全0时，浮点数下溢。
8 位移码表示的机器数为数的真值在数轴上向右平移了 128 个位置。

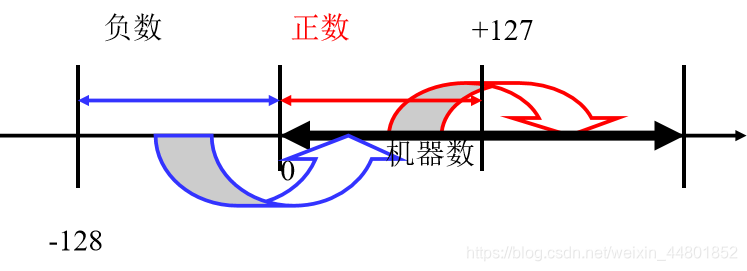
表示范围： 00000000 ~ 11111111

在移码中，最高位为0表示负数，最高位为1表示正数，这与原 码、补码、反码的符号位取值正好相反。
• 移码为全0时所对应的真值最小，为全1时所对应的真值最大！因此，移码的大小直观地反映了真值的大小，这将有助于两个浮点数进行阶码大小比较。
• 真值0在移码中的表示形式是唯一的，即：
[+0]移= [­0]移= 100…00
• 移码把真值映射到一个正数域，所以可将移码视为无符号数，直接按无符号数规则比较大小。
• 同一数值的移码和补码除最高位相反外，其他各位相同。

原码和补码
正数：
原、补码的编码完全相同；
负数：
符号位为1；
数值部分与原码各位相反，且末位加1；
补码和移码
无论正数还是负数：
符号位相反，数值位相同；

浮点数：小数点位置可变，形如科学计数法中的数据表示。
浮点数格式定义： N= Re× M
M：尾数(mantissa)，是一个纯小数，表示数据的全部有效数位，其位数决定着数值的精度；
R：基数(radix) ，可以取2、8、10、16，表示当前的数制；
微机中，一般默认为2，隐含表示。
e： 阶码(exponent) ，是一个整数，用于指出小数点在该数中的位置，其位数决定着数据的取值范围。
机器数的一般表示形式

一个十进制数可以表示成不同的形式

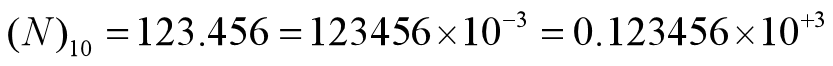
同理，一个二进制数也可以有多种表示：

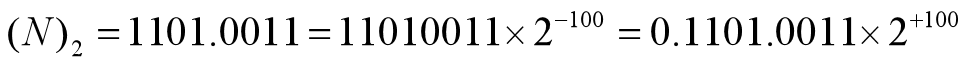
浮点数的表示
1.11×20=0.111×21=0.00111×23
规格化的目的
保证浮点数表示的唯一性；
保留更多地有效数字，提高运算的精度。
规格化要求：|尾数|≥0.5；
尾数原码表示：最高数值位为1，正数0.1…，负数1.1… ；
尾数补码表示：最高数值位和符号位相反，正数0.1…，负数1.0… ；
[+0.1B]补=0.10…0 [-0.1B]补=1.10…0 [-0.10…01B]补=1.01…11
规格化处理：
尾数向左移n位(小数点右移)，同时阶码减n； 左规
尾数向右移n位(小数点左移)，同时阶码加n。 右规

例子

请将数据-12.625D用16位的浮点数形式表示。
数据格式如下，阶码（含阶符）4位，尾数（含数符）12位

-12.625D = -1100.101 B = -0.1100 101×24 B
设尾数用原码表示，阶码用补码表示；
浮点数表示为： 0 100 ; 1.110 0101 0000
设尾数用补码表示，阶码用移码表示；
浮点数表示为： 1 100 ; 1.001 1011 0000

以16位数据为例，编码方式均采用补码表示
定点数
定点整数：-215~+215-1 （即-32768~+32767）
定点小数：-1~+1-2-15 （即-1~+0.999 9694 8242 1875）

浮点数
格式：
最大正数：+1111111×21111111B
最小正数：+0.0000001×2-1111111B
最大负数：-0.0000001×2-1111111B
最小负数：-1111111×21111111B

浮点数的表示要与具体的格式规定有关；
在做题时，要看题目里要求的浮点数格式和编码表示；
一般机器中，浮点数采用IEEE754标准来存放float、double类型的变量；
IEEE754标准只是浮点数的一种表示形式；

32位

数符S：表示浮点数的符号，占1位，0—正数、1—负数；
尾数M：23位，原码纯小数表示，小数点在尾数域的最前面；
由于原码表示的规格化浮点数要求，最高数值位始终为1，因此该标准中隐藏最高数值位(1)，尾数的实际值为1.M；
阶码E： 8位，采用有偏移值的移码表示；
移127码，即E=e+(27-1)=e+127；
标准8位移码应该是移128码，[x]移=x+27=x+128
浮点数的真值：N=（-1）S×（1.M）×2E-127

IEEE754 标准中的阶码E
正零、负零
E与M均为零，正负之分由数据符号确定；
正无穷、负无穷
E为全1，M为全零，正负之分由数据符号确定；
阶码E的其余值（0000 0001~1111 1110）为规格化数据；
真正的指数e的范围为-126~+127
为避免浮点数下溢，允许采用比最小规格化数还小的非规格化数来表示，但此时尾数M前的隐含位为0，而不是1。

float和double的精度是由尾数的位数来决定的；
float类型：223 = 8388608；
最多能有7位有效数字，但绝对能保证的为6位；
即float的精度为6~7位；
double类型：252 = 4503599627370496；
最多能有16位有效数字，但绝对能保证的为15位；
即double的精度为15~16位；

字符串形式
每个十进制数位占用一个字节；
除保存各数位，还需要指明该数存放的起始地址和总位数；
主要用于非数值计算的应用领域。
压缩的十进制数串形式
采用BCD码表示，一个字节可存放两个十进制数位；
节省存储空间，便于直接完成十进制数的算术运算；
用特殊的二进制编码表示数据正负，如1100—正、1101—负

字符的表示方法
非数值领域的问题：需要引入文字、字母以及某些专用符号，以便表示文字语言、逻辑语言等信息。
西文字符的编码
ASCII码
汉字的编码
输入码
数字编码、拼音码和字形码
机内码
用于汉字信息存储、交换、检索等操作

ASCII码(美国国家信息交换标准字符码)
包括128个字符，共需7位编码；
ASCII码规定：最高位为0，余下7位作为128个字符的编码。
最高位的作用：奇偶校验；扩展编码。
字符串
指连续的一串字符， 每个字节存一个字符。
当存储字长为2、或4个字节时，在同一个主存字中;
可按从低位字节向高位字节的顺序存放字符串的内容;
或按从高位字节向低位字节的次序顺序存放字符串的内容。

汉字的输入编码
目的：直接使用西文标准键盘把汉字输入到计算机 。
分类：主要有数字编码、拼音码 、字形编码三类。
汉字内码
用于汉字信息的存储、交换、检索等操作的机内代码。
如：GB2312、UNICODE编码。
汉字字模码
用点阵表示的汉字字形代码，用于汉字的输出。

数据校验原因
为减少和避免数据在计算机系统运行或传送过程中发生错误，在数据的编码上提供了检错和纠错的支持。
数据校验码的定义
能够发现某些错误或具有自动纠错能力的数据编码；
也称检错码；
数据校验的基本原理是扩大码距；
码距：任意两个合法码之间不同的二进制位的最少位数；
仅有一位不同时，称其码距为1。

码距及作用
设用四位二进制表示16种状态
16种编码都用到了，此时码距为1；
任何一种状态的四位码中的一位或几位出错，就变成另一个合法码；
无检错能力。
若用四位二进制表示8个状态
只用其中的8种编码，而把另8种编码作为非法编码；
可使码距扩大为2；
注意：并不是任选8种编码都可扩大码距；

奇偶校验码
根据数据中“1”的个数，设置1位校验位的值；
分奇校验和偶校验两种，只能检错，无纠错能力；
海明校验码
在奇偶校验的基础上，增加校验位而得；
具有检错和纠错的能力；
循环冗余校验码（CRC）
通过模2的除法运算建立数据信息和校验位之间的约定关系；
具有很强的检错纠错能力。

奇偶校验原理
在数据中增加1个冗余位，使码距由1增加到2；
如果合法编码中有奇数个位发生了错误，就将成为非法代码。
增加的冗余位称为奇偶校验位。
校验的类型
偶校验：每个码字(包括校验位)中1的数目为偶数。
奇校验：每个码字(包括校验位)中1的数目为奇数。
校验过程
发送端：按照校验类型，在发送数据后添加校验位P；
接收端：对接收到的数据（包括校验位）进行同样类型的校验，决定数据传输中是否存在错误；

设x＝( x0 x1…xn-1 )是一个n位字，则奇校验位Ｃ定义为
C ＝ x0⊕x1⊕…⊕xn-1
只有当x中包含有奇数个1时，C＝0
式中⊕代表按位半加(异或），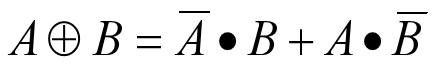

同理，偶校验位Ｃ定义为
C ＝ x0⊕x1⊕…⊕xn-1
即x中包含偶数个1时，才使C＝0

校验方法： （以偶校验为例）
发送： x0 x1…xn-1C （算出C加到需发送字的后面）
接收： x0 ’ x1 ’ …xn-1 ’ C ’
计算：F＝x’0⊕x’1⊕…⊕x’n-1⊕C ’
结果：若F＝1，意味着收到的信息有错；
若F＝0，表明x字传送正确
奇偶校验可提供单（奇数）个错误检测，
但无法检测多（偶数）个错误,
更无法识别错误信息的位置及纠正错误。
奇偶校验码常用于存储器读写检查，或ASCII字符传送过程中的检查。

海明码是1950年提出的；
只要增加少数的几位校验码，即可检测出多位出错，并能自动恢复一或几位出错信息；
实现原理：
在一个数据中加入几个校验位，每个校验位和某几个特定的信息位构成偶校验的关系；
接收端对每个偶关系进行校验，产生校验因子；
通过校正因子区分无错和码字中的n个不同位置的错误；
不同代码位上的错误会得出不同的校验结果；

确定校验位的位数
数据位数不同，所需的校验位位数也不同；
确定校验位的位置
数据位和校验位是交叉排列的；
校验分组
选择校验位和数据位的对应关系；
校验位的形成
由分组内的数据位形成对应的校验位；
接收端校验
接收端校验数据的正误；

设K为有效信息的位数，r为校验位的位数，则整个码字的位数N应满足不等式：
N＝K＋r≦2r－1
通常称为（N，K）海明码
设某(7,4)海明码表示的码字长度为 7 位，校验位数为 3 位。
例如：数据D3D2D1D0 =1001
K=4，r+5 ≦2r ；
可知，需要校验位3位P3P2P1 ;

数据表示
数据位D（DiDi-1…D1D0） 、校验位P（PjPj-1…P2P1）
海明码H （包括数据位和校验位）：HmHm-1…H2H1；
分组原则
每个校验位Pi从低到高被分在海明码中位号2i-1的位置；
例如：数据D3D2D1D0 =1001，校验位P3P2P1
海明码共7位H7H6…H2H1 ，各位分配如下：

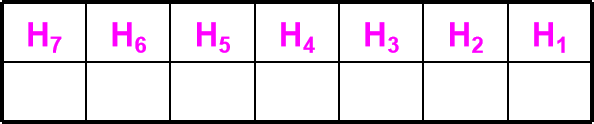
D3 D2 D1 P3 D0 P2 P1

校验原则
海明码的每一位Hi有多个校验位校验，其关系是被校验的每一位位号等于校验它的各校验位的位号之和；
每个信息位的位置写成用2的幂次之和的形式 ；
校验位形成公式
P1＝第一组中所有位(除P1)求异或
……
Pj ＝第j组中所有位(除Pj)求异或
为了能检测两个错误，增加一位校验Pj＋1，放在最高位。
Pj ＋1＝所有位(包括P1，P2 ，… ， Pj)求异或

接收端接收到数据后，分别求S1，S2，S3，…，Sj
S1＝第一组中所有位(包括P1)求异或
…
Sj＝第j组中所有位(包括Pj)求异或
Sj ＋1＝ Pj ＋1 ⊕所有位(包括P1，P2 ，… ， Pj)求异或
当Sj ＋1＝1时，有一位出错；
由Sj … S3 S2S1 的编码指出出错位号，将其取反，即可纠错。
当Sj ＋1＝0时，无错或有偶数个错（两个错的可能性比较大）；
当Sj… S3 S2S1 ＝ 0 … 0 00时，接收的数无错，否则有两个错。

同上例，接收端接收的数据为
接收端求S
S1＝0⊕1⊕0⊕1=0
S2＝0⊕1⊕0⊕1=0
S3＝1⊕1⊕0⊕0=0
S4＝1⊕1⊕0⊕0⊕1 ⊕1⊕0⊕0 =0
若接收端接收到错误的数据
S1＝0⊕1⊕0⊕1=0
S2＝0⊕1⊕1⊕1=1
S3＝1⊕1⊕1⊕0=1
S4＝1⊕1⊕1⊕0⊕1 ⊕1⊕0⊕0 =1

一个系统能纠正一位差错时，码距最小是3；
码距为3时，或能纠正一位错，或能检测二位错；
但不能同时纠正一位错并检测二位错。
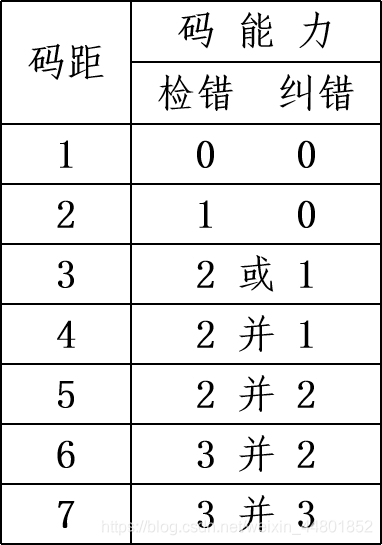
码距为1至7时，海明码的纠错和检错能力如右表：
码距越大，纠错能力越强，但数据冗余也越大，即编码效率低了。

2.2 定点加法、减法运算

补码加法运算基本公式
定点整数： [x+y]补 ＝[x]补 + [y]补 （mod 2n+1）定点小数： [x+y]补 ＝[x]补 + [y]补 （mod 2）
证明
（1）证明依据：补码的定义(以定点小数为例)

（2）证明思路：分三种情况。
(a) x、y均为正值（ｘ﹥0，ｙ﹥0）
(b) x、y均为负值（ｘ<0，ｙ<0）
© x、y一正一负（ｘ﹥0，ｙ﹤0 或者ｘ<0，ｙ>0）

证明：
(a)ｘ﹥0,ｙ﹥0
[ｘ]补＋[ｙ]补＝ｘ＋ｙ＝[ｘ＋ｙ]补　　　(mod 2)
(b)ｘ<0,ｙ<0
∵ [x]补=2+x , [y]补=2+y
∴ [x]补+ [y]补= 2+x+2+y =2+ (2+x+y)
= 2+[x+y]补 （mod 2）
= [x+y]补

©ｘ﹥0,ｙ﹤0 (ｘ<0，ｙ>0的证明与此相同)
∵ [x]补=x , [y]补=2+y
∴ [x]补+ [y]补= x+2+y =2+ (x+y)
当x+y>0时，2+(x+y) > 2 ，进位2必丢失；
因(x+y)> 0 ，故[x]补+[y]补= x+y =[x+y]补 (mod 2)
当x+y<0时，2+(x+y) < 2
因(x+y) < 0 ，故[x]补+ [y]补= 2+(x+y)
=[x+y]补 (mod 2)

补码减法运算基本公式
定点整数：[x - y]补＝[x]补 + [-y]补 （mod 2n+1）
定点小数：[x - y]补＝[x]补 + [-y]补 （mod 2）
证明：只需要证明 [－ｙ]补＝－[ｙ]补
已证明[x+y]补 ＝[x]补 + [y]补 ，故[y]补＝[x+y]补－[x]补
又[x－y]补 ＝[x]补 + [－y]补 ，故[－y]补＝[x－y]补－[x]补
可得[y]补 + [－y]补＝[x+y]补+ [x－y]补－[x]补 －[x]补
＝[x + y + x－y]补－[x]补 －[x]补
＝[x + x]补－[x]补 －[x]补＝0

[－ｙ]补等于[ｙ]补的各位取反，末位加1。

[例13] 已知ｘ1＝ － 1110，ｘ2＝ + 1101， 求：[ｘ1]补，[－ｘ1]补，[ｘ2]补，[－ｘ2]补

解：
[ｘ1]补 ＝1 0010
[－ｘ1]补＝﹁ [ｘ1]补＋1
＝0 1101＋0 0001＝0 1110
[ｘ2]补 ＝0 1101
[－ｘ2]补＝﹁[ｘ2]补＋1
＝1 0010＋0 0001＝1 0011

定点数补码加减法运算

基本公式
定点整数： [x ± y]补 ＝ [x]补 + [± y]补 （mod 2n+1）
定点小数： [x ± y]补 ＝ [x]补 + [± y]补 （mod 2）
定点数补码加减法运算
符号位和数值位可同等处理；
只要结果不溢出，将结果按2n+1或2取模，即为本次运算结果。

溢出
在定点数机器中，数的大小超出了定点数能表示的范围。
上溢
数据大于机器所能表示的最大正数；
下溢
数据小于机器所能表示的最小负数；
例如，4位补码表示的定点整数，范围为[-8，+7]
若x = 5，y = 4，则x+y产生上溢
若x = -5，y = -4，则x+y产生下溢
若x = 5，y = -4，则x-y产生上溢

方法1——直接判别法

方法：
同号补码相加，结果符号位与加数相反；
异号补码相减，结果符号位与减数相同；
特点：硬件实现较复杂；
举例：
若[x]补=0101，[y]补=0100，则[x+y]补=1001 上溢
若[x]补=1011，[y]补=1100，则[x+y]补=0111 下
若[x]补=0101，[y]补=1100 ，则[x-y]补=1001 上

方法2——变形补码判别法

变形补码，也叫模4补码：采用双符号位表示补码

特点：硬件实现简单，只需对结果符号位进行异或
举例：
若[x]补=00101，[y]补=00100，则[x+y]补=01001
若[x]补=11011，[y]补=11100，则[x+y]补=10111
若[x]补=00101，[y]补=11100 ，则[x-y]补=01001

方法3——进位判别法

判别方法：
最高数值位的进位与符号位的进位是否相同；
判别公式
溢出标志V=Cf ⊕ Cn-1
其中Cf为符号位产生的进位， Cn-1为最高数值位产生的进位

2.3 定点乘法运算

串行乘法

乘法运算 ＝ 加法＋移位。
若乘数数值位n = 4，则累加 4 次，移位4 次；
乘法过程
由乘数的末位决定被乘数是否与原部分积相加;
被乘数只与部分积的高位相加
部分积右移一位形成新的部分积;
同时乘数右移一位（末位移丢）;
空出高位存放部分积的低位。
硬件构成
3个具有移位功能的寄存器、一个全加器

原码乘法（符号位和数值位必须分开计算）
原码一位乘
一次判断1位，需判断n次（乘数位数为n）；
原码两位乘
一次判断2位，可提高乘法的运算速度；
补码乘法（符号位和数值位可以等同处理）
补码一位乘
结果修正法——需区分乘数正负号，复杂
Booth算法——比较法，符号位直接参与运算
补码两位乘

原码一位乘法
设X＝Xf . X1X2…Xn， Y＝Yf . Y1Y2…Yn，乘积的符号位为Pf，则 Pf＝Xf⊕Yf |P|＝|X|●|Y|
求|P|的运算规则如下
被乘数和乘数均取绝对值参加运算，符号位单独考虑；
被乘数取双符号位，部分积的长度同被乘数，初值为0；
从乘数的最低位Yn开始判断：
若Yn＝1，则部分积加上被乘数|X|，然后右移一位；
若Yn＝0，则部分积加上0，然后右移一位。
重复，判断n次

两位乘
原码乘
符号位和数值位部分分开运算；
两位乘
每次用乘数的2位判断原部分积是否加和如何加被乘数；

运算规则如下
符号位单独运算，最后的符号Pf＝Xf⊕Yf。
部分积和被乘数均采用三位符号位；
乘数末位增加1位C，其初值为0，运算过程见表；
乘数字长与运算步骤
若乘数字长为偶数（不含符号），最多做n/2+1次加法，需做n/2次移位，最后一步不移位；
若尾数字长n为奇数（不含符号），增加一位符号0，最多做n/2+1次加法，需做n/2+1次移位，最后一步右移一位。

补码一位乘法

设被乘数[x]补 = x0 . x1x2 … xn ，乘数[y]补 = y0 . y1y2 … yn
若被乘数任意，乘数为正

统一的补码乘法公式

[xy]补 = [x]补 （0. y1y2 … yn ）－ [x]补 ● y0

乘数[y]补，去掉符号位，操作同 ① ；
运算完成后，需对结果加[–x]补校正；
公式为： [xy]补 = [x]补 （0. y1y2 … yn ）－ [x]补

补码两位乘法

运算规则如下
符号位参加运算；
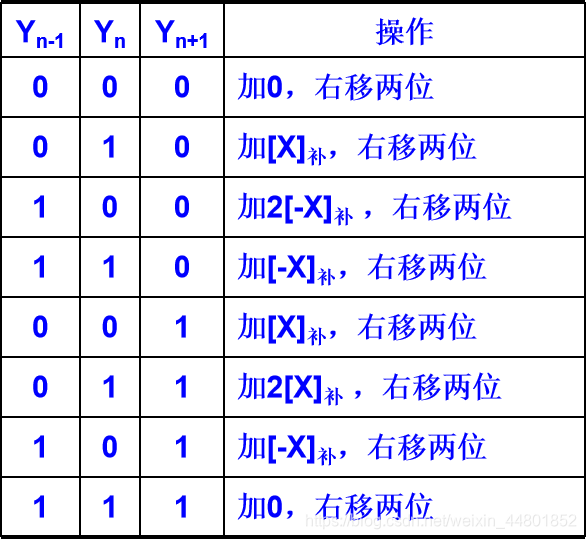
部分积和被乘数均采用三位符号位，乘数采用双符号位，末位增加1位Yn+1，其初值为0；
按右表操作；
若尾数字长n为偶数（不含符号），乘数用双符号位，最后一步不移位；若尾数字长n为奇数（不含符号），乘数用单符号位，最后一步移一位。

原码并行乘法

不带符号的阵列乘法器
设有两个不带符号的二进制整数：
A＝am-1…a1a0 ； B＝bn-1…b1b0
它们的数值分别为a和b，即


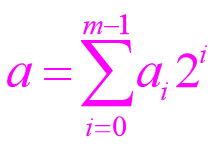
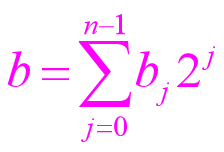
A、B相乘，产生m＋n位乘积P：
P＝pm+n-1…p1p0
乘积P 的数值为

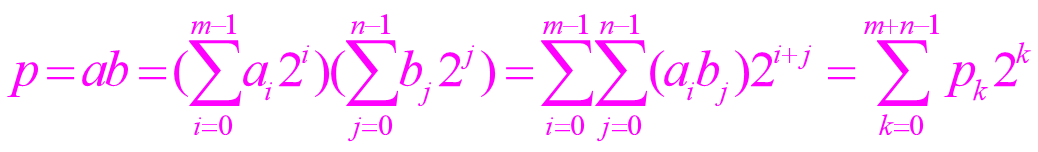
带符号的阵列乘法器

带符号原码的乘法：
设有两个n+1位带符号的二进制整数：
A＝an…a1a0 ； B＝bn…b1b0
乘积AB=(an⊕bn)(an-1…a1a0 bn-1…b1b0)
带符号数的阵列乘法器电路：
在无符号数的阵列乘法器的基础上完成；
使用3个求补器，分别用对应的符号位控制；
2个算前求补器：将乘数真值的绝对值送入运算器；
1个算后求补器：将负的乘积的真值求出补码表示；
称为间接补码乘法电路。

对2求补电路的原理

设有两个n+1位带符号补码： A＝an…a1a0 ； B＝bn…b1b0
采用原码乘法电路计算A*B
符号位不参与运算，只用于确定结果的符号；
数据位要取绝对值参与运算： 正数——不变；负数——各位取反，末位加1
对2求补电路：
数据举例： [-2]补 =1110 [-3]补 =1101 [-6]补 =1010 [+2]补=1010 [+3]补=0011 [+6]补=0110
两相反数的补码特征：自右向左，第一个“1”的右侧所有数据位，均相同； 左侧所有数据位，均相反。

2.4 定点除法运算

(1) 在计算机中，小数点是固定的，不能简单地采用手算的办法。为便于机器操作，除数Y固定不变，被除数和余数进行左移 (相当于乘2)
(2)机器不会心算，必须先作减法： 若余数为正，才知道够减；若余数为负，才知道不够减。不够减时必须恢复原来的余数，以便再继续往下运算。这种方法称为恢复余数法。
(3) 要恢复原来的余数，只要当前的余数加上除数即可。但由于要恢复余数，使除法进行过程的步数不固定, 因此控制比较复杂。
实际中常用不恢复余数法，又称加减交替法。其特点是运算过程中如出现不够减，则不必恢复余数，根据余数符号，可以继续往下运算，因此步数固定，控制简单。

除法的数据约定

设n位被除数和除数用定点小数表示
　被除数 　[ｘ]原＝ｘf .ｘn－1…ｘ1ｘ0
　 除数 [ｙ]原＝ｙf .ｙn－1…ｙ1ｙ0
则商 [Q]原＝(ｘf⊕ｙf)＋(0.ｘn－1…ｘ1ｘ0)/(0.ｙn－1…ｙ1ｙ0)
式中，ｘf为被除数符号，ｙf为除数符号。
约定
小数定点除法 |x| ＜ |y|，整数定点除法 |x| ＞ |y|
避免商溢出
被除数不等于 0，除数不能为 0

恢复余数法

被除数减除数，够减时，商1；不够减时商0。
由于商0时若不够减，即不能作减法，但现在在判断是否商0时，已经减了除数，为了下次能正确运算，必须把已减掉的除数加回去恢复余数。这就是“恢复余数法”。
【例1】x=0.1001, y=0.1011, 用恢复余数法求 x/y.
解：[x]原 =[x]补= x=０.1001,
[y]补=0.1011, [-y]补=1.0101

恢复余数法运算规则

余数 Ri＞0 上商 “1”，2Ri – |y|
余数 Ri＜0 上商 “0”， Ri + |y| 恢复余数
2( Ri+|y|) – |y| = 2Ri + |y|

不恢复余数法运算规则
上商“1” 2Ri – |y|
上商“0” 2Ri + |y|

原码加减交替法的运算规则
运算规则：
符号位不参加运算，取双符号位；
用被除数减去除数：
当余数为正时，商上1，余数左移一位，再减去除数；
当余数为负时，商上0，余数左移一位，再加上除数。
根据余数的正负，再做如上处理（上商、加减除数）
当第n+1步余数为负时，需加上|Y|得到第n+1步正确的余 数，最后余数为rn×2-n（余数与被除数同号）。

2.5 定点运算器的组成

四种基本的逻辑运算：
逻辑非、逻辑加（或）、逻辑乘（与）、逻辑异（异或）
算术运算与逻辑运算的差别：是否考虑进位
算术运算： 每一位运算都需要考虑前一位的进位状态；
逻辑运算：每一位运算都是独立进行的，不考虑进位；

一位全加器(FA)的逻辑表达式为：
Fi＝Ai⊕Bi⊕Ci Ci＋1＝AiBi＋BiCi＋CiAi
ALU设计思想：
Ai和Bi先转换为组合函数Xi和Yi；
该转换过程由参数S0S1S2S3控制；
由Xi，Yi和Ci进行全加器运算。
ALU的运算讨论
算逻运算单元的逻辑式： Fi=Xi⊕Yi⊕Ci Ci+1=XiYi+YiCi+XiCi

ALU运算讨论
S1S0=00，S3S2=00
Yi=﹁Ai，Xi=1
Fi=Xi⊕Yi⊕Ci = 1⊕﹁Ai⊕Ci= Ai⊕Ci
S1S0=11，S3S2=11
Yi= 0，Xi= ﹁ Ai
Fi=Xi⊕Yi⊕Ci = (﹁Ai)⊕0⊕Ci= (﹁Ai) ⊕Ci
S1S0=01，S3S2=00
Yi=﹁Ai﹁Bi，Xi= 1
Fi=Xi⊕Yi⊕Ci = 1⊕(﹁Ai﹁Bi)⊕Ci= (Ai +Bi) ⊕Ci
……

控制端
S0~S3 ：控制ALU的运算方式，如加1、A和B相加等；
M ：控制ALU的运算类型——算术运算、逻辑运算；
逻辑运算M=1，封锁Ci，送入Fi输入端的Ci=0；
算术运算M=0，Ci正常参与运算；
74181 ALU芯片有正逻辑、负逻辑之分
Cn、P、G、Cn+i等信号的逻辑状态不同；
具体的逻辑功能含义有差别；

先行进位ALU
串行加法器(行波加法器)：
结构形式：将n个全加器级联，得到n位加法器；
特点：进位逐位传递，速度慢。
超前进位加法器：设计依据为进位产生公式
结构形式
多片先行进位加法器级联而成；
片内先行进位，片间采用先行进位部件成组进位；
特点
和的所有位可同时计算，运行速度快。

由Ci+1=XiYi + YiCi + XiCi推导：
Ci+1 = XiYi + ( Xi + Yi ) Ci = Gi + Pi Ci
Gi = XiYi为进位产生函数；Pi = Xi+Yi为进位传递函数；
假设4位的ALU，加数X3X2X1X0和Y3Y2Y1Y0、低位进位C0
C4 = G3+P3C3
= G3+P3 (G2+P2C2)
= G3+P3 (G2+P2((G1+P1C1)))
= G3+P3 (G2+P2((G1+P1(G0+P0C0))))
内部总线
根据总线所在位置分
内部总线： 指CPU内各部件的连线。
外部总线： 指系统总线，即CPU与存储器、I/O系统之间的连线。
按总线的逻辑结构分
单向总线： 信息只能向一个方向传送。
双向总线： 信息可以分两个方向传送，既可以发送数据，也可以接收数据。

单总线结构的运算器
同一时间内，只能有一个操作数放在单总线上。
缺点：操作速度较慢 。
优点：控制电路比较简单。
双总线结构的运算器
两个操作数同时加到ALU进行运算。
三总线结构的运算器
ALU的两个输入端分别由两条总线供给；
ALU的输出则与第三条总线相连。

2.6 浮点运算方法和浮点运算器

设有两个浮点数X = Mx×2Ex 和 Y = My×2Ey ，且Ex> Ey
若要求X±Y的结果S，则
S =X±Y =MS×2ES
其中 ，ES =Ex，MS =Mx±(My SHR (Ex - Ey))

两操作数对阶

对阶的原则
以较大的阶码为标准，调整阶码较小的数据；
避免阶码较大的浮点数的尾数左移，导致最高有效数位丢失；
具体操作
求阶差△E ＝ EX－EY
调整阶码较小的数据
若△E >0，则MY右移△E位，结果的阶码为EX
若△E <0，则MX右移|△E|位，结果的阶码为EY
例，X——EX=0 001，MX=0.101；Y——EY=0 011，尾数MY=0.111
阶差△E ＝ EX－EY = 0 001-0 011 = - 10
X尾数MX右移2位， MX=0.001 01

浮点数加减运算——结果的规格化处理
两尾数加减的结果有两种情况
尾数溢出
尾数右移1位，阶码加1
尾数为非规格化数据
尾数左移1位，阶码减１，直至数值位最高位与符号位相反。
接上例，对阶后E=EY=0 011，尾数MX=0.001 (01)，MY=0.111
尾数求和MS = MX + MY = 00.001 01 + 00.111 = 01.000 01
两符号位相反，应进行右规1位的操作
则MS = 00.100 (001) ， ES= 011+1= 0 100

浮点数加减运算——结果的舍入处理

在对阶或右规操作时，会使加数或结果的尾数低若干位移出，影响精度，常用两种舍入处理方法
方法１：０舍１入法
保留右移时的移出位，若最高位为１，则尾数加１；否则舍去；
特点：精度较高，但需要记录所有的移出位。
方法２：恒置１法
若之前步骤有右移操作，则直接将结果的最低位置1;
特点：精度较0舍1入法较低，但应用简单。
接上例，结果的尾数MS = 00.100 001
０舍１入法： MS = 00.100
恒置１法： MS = 00.101

浮点数加减运算——结果的溢出判断

尾数溢出
在规格化处理时，通过完成右规完成；
阶码溢出
上溢(结果绝对值太大)——置上溢标志，结束；
下溢(结果绝对值太小)——置机器零；
正常——运算结束；
接上例， 运算结果的阶码ES= 011+1= 0 100
未溢出！

浮点乘法、除法运算

流水线原理
把输入的任务分割成一系列子任务，使各个子任务能在流水线的各个阶段并发地执行。
实际上是在计算机上实现时间并行性的一种非常经济的方法。