判断链表是否有环并求环的入口和环的长度

本文主要是介绍判断链表是否有环并求环的入口和环的长度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

方法：

1. 求链表是否有环，最直观的方法是从头结点的地址开始，把下一个地址都取出来，然后比对，是否有相同的。但这个方法需要两两比较，算法时间复杂度较高。
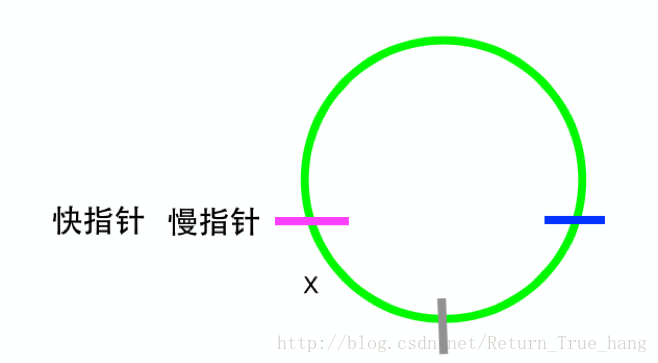
2. 更好的一个做法是快慢指针（慢指针一次前进一个地址，快指针一次前进两个地址）同时从头结点出发，只有链表有环存在，则它们必定会相遇。
3. 快慢指针算法有一个注意点，慢指针进入环之前，快指针可能已经在环中绕了几次圈了。
4. 首先比较简单的是求环的长度，当快慢指针第一次相遇，可以确定的一点是它们一定都在环中，那么按照它们原先的速度绕圈，当第二次相遇的时候，环的长度就出来了。
5. 求环的入口相对比较难想到，要分段来求，(假设 a 是从头结点到环入口，r是环周长)
   A. 假设慢指针刚刚到达环入口，此时快指针在距离环入口 x 处。这一点能给到我们的信息是 a = x + nr (n=1,2,3,4)
   
   B. 从这点之后，实际上问题转化成在环上，快指针去追慢指针，而追击的距离变成环的长度，y - x 的距离。由于速度差是1，很明显被追到的时候，慢指针走过y-x的距离，也就是慢指针距离环入口 x 的距离。
   C. 从相遇的这个地方开始，慢指针继续走 x + nr ，即 a 的距离，则到达环入口。所以我们只需同时从头指针出发一个慢指针，两者相遇即为环入口。

看完思路可以去实现一波： 牛客地址

class Solution {
public:ListNode* EntryNodeOfLoop(ListNode* pHead){ListNode * fast=pHead;ListNode * slow = pHead;//快指针和慢指针在头结点开始跑，第一次相遇停下while(fast != NULL && fast->next != NULL){slow = slow->next;fast = fast->next->next;if(fast == slow) {//第二个慢指针从头结点出发ListNode * slow2 = pHead;while(slow2 != slow) {slow2 = slow2->next;slow = slow->next;}return slow;}}return NULL;}
};

这篇关于判断链表是否有环并求环的入口和环的长度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---