本文主要是介绍Cuckoo Search,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
杜鹃鸟搜索(Cuckoo Search)是2009年发表在nature(见参考文献1)上的又一种仿生物智能优化算法。该算法主要根据杜鹃鸟的孵育寄生(obligate brood parasitism)的特征,杜鹃的这种孵育行为表现在:
Cuckoo breeding behavior
杜鹃鸟通过寄生在其他鸟类(或同类不同种的)巢穴孵化得以繁殖的。例如 Tapera,就具有很好的外形、颜色模仿能力,可以安全的藏身在其他鸟类巢穴中。除了模仿能力以外,杜鹃鸟的蛋会比原来巢穴中的蛋孵化的早,这样待哺的机会更多。
CS伪代码
根据杜鹃的特点,CS算法设计伪代码如下:
大意是可以理解为:
begin
//目标函数为f(x),xi表示解,n个巢,Pa为host发现cuckoo eggs新建巢的概率
随机初始化xi(1,2,....n)赋给host_nests,且符合取值范围;
while(未超出设定的最大迭代次数or未达到可容忍的目标值)通过Levy flight产生n个新杜鹃占用巢new_nests;计算host_nests和new_nests的fitness;For 对每一个nest jif(F(new_nests_j)>F(host_nests_j))在j上用new_nests替换相应的host_nests;endendif(随机数>Pa)随机选取host_nests里面的几个nests,用偏差随机游走生成新巢new_nests1;endFor 对每一个nest jif(F(new_nests1_j)>F(host_nests_j))在j上用new_nests1替换相应的host_nests;endend找出best nest;end while
输出最优解;
end(1)杜鹃鸟蛋孵化之后可以赶走原本鸟巢中的蛋,这对应于启发式优化算法中的local search,使用Levy walk可以加快这个搜索过程(产生的新解既可以继承当前最优解,又可以不局限于局部最优);
(2)杜鹃鸟蛋藏身处被巢穴的主人发现,摧毁巢穴并建立新巢,这对应于优化算法中的类似于选择变异的效果(个人认为),这里运用biased random walk。
random walk
随机游走是包含一连串随机步长的随机过程。
Sn = Sn-1 + Xn
Sn为n个随机步态的和
Xn为第n个步长,服从某一随机概率分布
即下一个状态Sn只与前一个状态Sn-1以及移动步长Xn有关,符合马尔科夫链的主要特性。
Levy flight
如果一个random walk的步长服从Levy distribution,那么这个random walk就叫做Levy flight or Levy walk。Levy flight实际上是步长服从均值为0,方差为delta(t)^2的正态分布,其中方差delta(t)^2是可变的。在CS算法中用到的Levy flight是参考自Mantegna:Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes在1994年提出的算法。
设随机变量s表示步长,令
u,v分布为两个服从正态分布的独立随机变量
其中
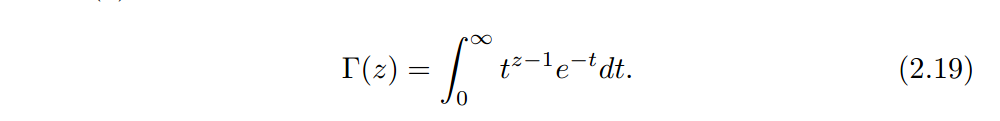
1、在Local search过程中,(1) step_size = 0.01 * P(s) *(当前解与最好解之差);
s表示Levy flight的步长随机变量,P(s)为服从Levy fdistribution每次对应的概率,该分布即由上述公式2.21求得,
当前解与最好解之差作为步长取值范围,
0.01是根据解的取值范围而定的,以免发生过随机。
CS的demo中对于新巢计算(2) s = s + step_size * randn(size(s));
step_size * randn(size(s))表示方差为step_size^2,均值为0的服从正态分布的随机数。
2、在选择变异nest值时,(1)step_size = rand * (任意选取两个解之差);
(2)new_nests = nests + step_size;
step_size表示服从[0,任意选取两个解之差]的均匀分布的随机数。
参考文献:
1 Cuckoo Search via L´evy Flights
2 Engineering Optimisation by Cuckoo Search
3 Nature-Inspired Metaheuristic Algorithms
继续坚持写博客,最近得抓紧啦,加油哇!!!
这篇关于Cuckoo Search的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!

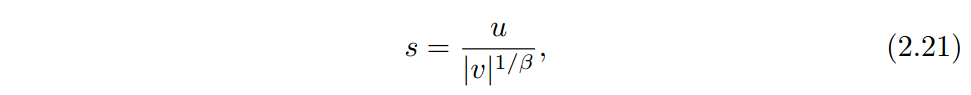
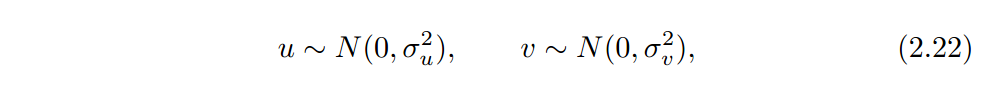
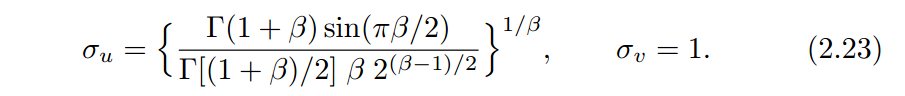







![[LeetCode] 240. Search a 2D Matrix II](/front/images/it_default2.jpg)
