考公行测笔记

一、判断推理–图形

1.1图形推理（位置规律、样式规律、属性规律、特殊规律、数量规律、空间重构)

1.1.1位置规律

图形特征：元素组成基本相同

1.1.1.1 平移

1. 方向：直线（上下、左右、斜对角线），绕圈（顺时针、逆时针）
2. 常见步数：恒定、递增

1.1.1.2旋转

1. 方向：顺时针、逆时针
2. 常见角度：45°、90°、180°等

1.1.1.3 翻转

1. 左右翻转：两图沿竖轴对称
2. 上下翻转：两图沿横轴对称

1.1.2 样式规律

图形特征：元素组成相似

1.1.2.1 加减同异

图形特征：元素组成相似，且相同线条重复出现

1. 相加、相减
2. 求异：去掉相同线条，保留不同线条
3. 求同：去掉不同线条，保留相同线条

解题思路：找1-2条线段看他们经变化后是什么状态，然后对比选项找差异，有时候可能结合位置做考察

1.1.2.2 黑白运算

1、图形特征：图形轮廓和分割区域相同，且黑块数量不成规律
2、解题方法：按照对应位置进行“黑白”相加运算，将所得规律应用于所求图形
3、区分:

黑块数量相同:优先平移
黑块数量不同:优先黑白运算

4、小技巧

1.对比选项找差异
2.大块面积一起看（随缘)

1.1.3 属性规律

图形特征：元素组成不相同、不相似

1.1.3.1 对称性

1、轴对称 特征图：“等腰”图形
2、中心对称（图形旋转 180°后和原图形完全重合）特征图：平行四边形，“S”“N”“Z”及其变形图等
3、轴对称 + 中心对称特征图：有两条相互垂直的对称轴的图形
4、对称性的考法

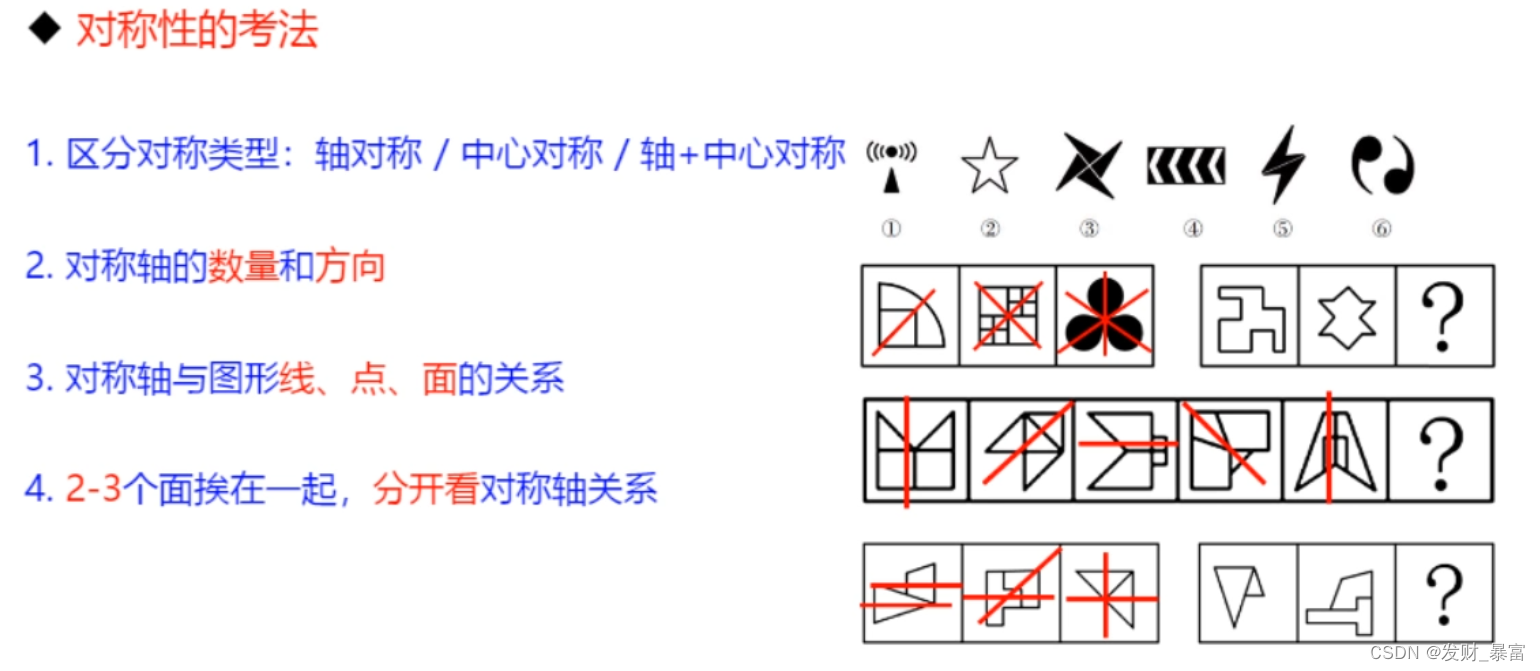
牢记“对称轴数量”的题目特征:等边三角形(三足鼎立)

1.1.3.2 曲直性

全曲、全直、曲+直

1.1.3.3 开闭性

1、全开、全闭、半开半闭；
2、特征图：出现生活化或粗线条图形，考虑开闭性

1.1.4 特殊规律

1、图形特征：多个封闭图形连在一起，多个面连在一起─优先分开看对称、再看公共边

1.1.4.1 图形间关系

1. 相离

2. 相交
   （1）相交于点
   （2）相交于线

    相交边的数量相交边的样式（长 / 短、整体 / 局部、曲/直）
   

   （3）相交于面

    相交面的形状、属性相交面与图形的关系
   

1.1.4.2 功能元素

图形特征：题干每幅图都出现小黑点、小白点、箭头等小元素
标记位置：
（1）点：直直交点 / 曲曲交点 / 曲直交点
（2）线：直线 / 曲线、最长线 / 最短线
（3）角：直角 / 锐角 / 钝角、最大角 / 最小角
（4）面：重合面 / 单独面、最大面 / 最小面、形状、属性

1.1.5 数量规律

“数量规律”图形特征：元素组成不同，且属性没规律；数量特征图明显

【注意】（1）元素组成不同，优先考虑属性规律，属性无规律，考虑数量规律。（2）数量特征特别明显，可以考虑数量规律。

考点：点、线、角、面、素
面：白色的封闭区域

空间重构
类比推理
定义判断
逻辑判断（翻译推理)
逻辑判断（组合排列、日常结论)逻辑判断（削弱论证)
逻辑判断（加强论证、原因解释)
当前页面22条主题 共257字