Bit Manipulation —— LeetCode题解Single-number系列

Bit Manipulation需要把每一个变量都想象成一串二进制编码，用and,
or, not等逻辑进行运算。在single-number系列的题中，需要把int想象成一串32位的二进制编码。所以所这种题要先转换成二进制的思维。解法的确需要“取巧”，如果没有见过此类题的话还挺难想出来的。

Single-number

Given an array of integers, every element appears twice except for
one. Find that single one.
Note: Your algorithm should have a linear
runtime complexity. Could you implement it without using extra memory?

这里重点需要掌握异或运算（XOR）。

• 每个数XOR 0就是它本身
• 每个数XOR它本身是0
• XOR符合交换律

将给定的数两两进行异或运算，由于满足交换律，所以A^B^C^B^A =
A^A^B^B^C，也就是说可以看成所有出现两次的数XOR自身变成0，最后再用0 XOR那个出现一次的数，得出的结果就是出现一次的数。

想通原理之后代码超简单，一个loop就搞定了。

public class Solution {public int singleNumber(int[] A) {int res = 0;for(int i:A){res = res^i;}return res;}
}

另一种角度：这使我忽然想到了最强大脑的层叠消融。把每个int想象成一个set，就是在32位里1出现的位置的集合。那么每两个int代表的set可能有重叠或者没有。然后在两个int XOR的时候，这两个set都没有覆盖或者都覆盖的地方因为“奇消偶不消”的原则，清零了，只被一个set覆盖的地方会保留。那么把给定的数两两XOR之后，那些出现两次的数一定会给某些区域贡献两次，所以就抵消了。最后依然保留下来的位置，是得到了奇数次的贡献，于是这些位置就是answer的二进制编码中 1出现的位置。

Single-number (ii)

Given an array of integers, every element
appears three times except for one. Find that single one.
Note: Your algorithm should have a linear
runtime complexity. Could you implement it without using extra memory?

上一题当中XOR自动帮我们实现了“同一位置得到两次贡献就清零”的功能。现在这个题需要手动实现“同一位置得到三次贡献就清零”。我们需要维持三个set （其实就是三个int），分别代表哪些位置上出现过一次1，出现过两次1，和出现过三次1。出现到四次就自动回到一次那个set。用到的依旧是逻辑运算。

这三个set的名称分别是：one, two, three。A代表每一轮迭代新看到的int

每一次迭代进入到新的two里面的是 A&One 以及 Two里面排除(A&Two) 的部分。Two里面排除A&Two用逻辑运算来写就是 Two^(A&Two)

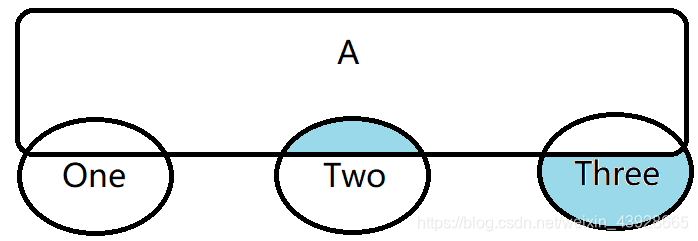
Similarly，一次迭代进入到新的three里面的是 A&Two 以及 Three里面排除(A&Three) 的部分( (A&Three)^Three ).

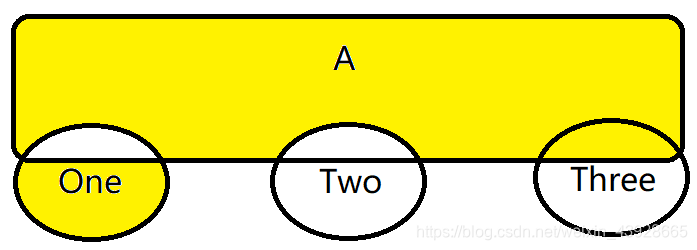
每一次迭代进入到新的one里面的多了一项，包括 A&Three , One里面排除(A&One) 的部分，还有 A里面排除one&A, two&A, three&A 的部分。注意，由于one, two, three彼此之间没有重叠，所以“A里面排除one&A, two&A, three&A” 就可以用A^(A&one)^(A&two)^(A&three)表示。

逻辑通了之后代码依旧超简单，只要每一轮根据A和上一轮的one, two, three 得到新的one, two, three，进行update即可。全部迭代完之后one这个set就代表那个只出现一次的int的二进制表示中1出现的位置。（最后的one就是answer）

注意：boolean之间的运算是 | |，&&这样，但int之间做bit
manipulation就是^, |, &，都是单个。

public class Solution {public int singleNumber(int[] A) {int one = 0;int two = 0;int three = 0;for(int i:A){int new_one = (i & three) | one^(i & one) | i^(i&one)^(i&two)^(i&three);int new_two = (i&one) | two^(i&two);int new_three = (i&two) | three^(i&three);one = new_one;two = new_two;three = new_three;}return one;}
}

Single-number (iii)

(牛客上面没有这道题，是leetcode官网找到的，难度比前两道题又有所提升) Given an array of numbers nums, in which exactly two elements
appear only once and all the other elements appear exactly twice. Find the two
elements that appear only once.
For example, Input: [1,2,1,3,2,5]; Output:[3,5]
Note:

1. The order of the result is not
   important. So in the above example, [5, 3] is also correct.
2. Your algorithm should run in linear
   runtime complexity. Could you implement it using only constant space
   complexity?

思路：先把所有的数都XOR一遍，得到的是只出现一次的那两个数不重叠的部分
（也就是answer_1 ^ answer_2）。我们希望按照某个规矩把所有的数分组，并且要保证，1）同样的数要分到同一组，2）只出现一次的两个数需要分到不同的组。这样对两个组分别进行single-number的算法就可以找出它们俩。

那么该怎样分组呢？

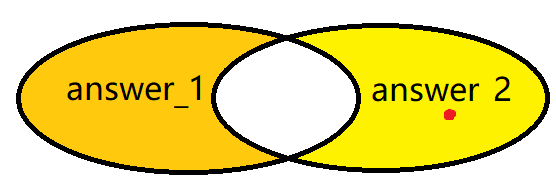
如图，把所有数字都XOR一遍之后，得到的是上图带颜色的部分。然后我们希望从浅黄色部分（桔黄色的也行，这俩顺序没有分别）找到一个位置，只有answer_2在这个位置上的bit是1，answer_1在这个位置上的bit是0。

于是，我们可以把在这个位置上bit是1的数分到第一组，在这个位置上bit是2的数分到第二组。这种分组方式可以满足上述的两个要求。

class Solution {public int[] singleNumber(int[] nums) {int temp = 0;for(int i:nums){temp = temp^i;}/*int one = 1; //find a bit s.t. temp has ‘1’ on that bit. For initialization,the smallest bit is set to 1.while ((one&temp)!=one){one <<= 1; // 如果temp在这一位上不是1,就shift to left一位}*/int one = temp&(-temp);// 从大神那里看到a&(-a)就是从最小位开始算第一个是1的位// 因为a算负数是先将二进制取反然后+1.// 开始分组boolean[] group = new boolean[nums.length];for(int i=0; i<nums.length; ++i){if ((nums[i]&one) == (temp&one)){group[i] = true;}else {group[i] = false;}}//把每个组里的数互相XOR一遍int answer_1 = 0;int answer_2 = 0;for(int i=0; i<nums.length; ++i){if(group[i]) {answer_1 = answer_1^nums[i];}else {answer_2 = answer_2^nums[i];}}int[] answer = new int[2];answer[0] = answer_1;answer[1] = answer_2;return answer;}
}

参考链接：https://www.cnblogs.com/grandyang/p/4741122.html