Codeforces Round #626 (Div. 2, based on Moscow Open Olympiad in Informatics)

Codeforces Round #626 (Div. 2, based on Moscow Open Olympiad in Informatics)

A. Even Subset Sum Problem

• 题意：这一题就是给一个序列，问能这个序列的子集的和，能否为偶数

• 代码

#include<iostream>
#include<vector>
using namespace std;const int Len = 1e6 + 5;int main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);//freopen("A.txt","r",stdin);int t;cin >> t;while(t --){int n;cin >> n;int ar[n + 5];for(int i = 1; i <= n; i ++) cin >> ar[i];if(ar[1] & 1){if(n < 2) cout << -1 << endl;else if(ar[2] & 1)  cout << 2 << endl << 1 << ' ' << 2 << endl;else cout << 1 << endl << 2 << endl;}elsecout << 1 << endl << 1 << endl;}return 0;
}

• 收获：明白 了 & 操作符号的意思

B. Count Subrectangles

• 题意：给两个数组a【】、b【】，又有一个 c[ ][ ] 二维数，在这个二维数组中的元素为：c[ i ][ j ] = a[ i ] * b[ i ],
  问面积为k的矩形在c[ ][ ]中有多少个（⚠️ ：构成这个矩形的所有元素必须是全由1组成）

• 思路: ----> ⬇️方

• 代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#include<map>
#include<vector>
using namespace std;
/** 思路：这一题的思路：就是遍历所有的 k 的所有除数对，进行找答案。*      但是直接暴力找答案明显会时间超时，所以这一题的难点就是 “预处理”，*      在预处理的的时:*      1. 首先我们一定要明白题目上给的一些 数据 的用途，*      首先我们考虑 在数组a中在假设区间[x, y]内全部是1，假设这个时候数组b中全部为 1，*      我就一定可以确定c数组中，对应的在 x行到y行 这些行必定都是由 1 组成，*      那么说明我们可以把c中 x到y行之间的距离预处理下来，这些距离就是可以作为矩形的高度*      而对于一个 在数组a中的这个[x, y] 区间，我们可以统计出来, 高度为h（h属于[1, y - x + 1]）*      的方案个数.*      2. 我们假设 a数组中的数全部是1，那么我在考虑 b数组连续为1的区间[i, j], 那么对应于c数的中的*      i 到 j 列之间的每一列都是由 1 组成，同样我们可以预处理出所有的宽度 w 的方案个数*      3. 之前我们在考虑 一个数中的 连续为1的情况总是 把另一个数组中的 元素全部当成1来处理，*      但这是与题上的实际情况不符合的，但是我们的统计确实有用的，我们可以做一个假设来考虑，*      我们假设要组成一个 高h = 2， 宽 w = 3 的一个矩形，那么在数组a中连续两个1，在c中所对应的行，*      与在数组b中连续3个1 在c中所对应的列, 在连续的列与行的交叉处我们一定可以保证 这个2x3的矩形交叉的区域全部*      是有1 组成，就是我要求的这个矩形，，剩下的就是看代码列。。。。*/
#define ll long long vector<ll> gao(vector<int> a)
{int n = a.size();int i = 0;vector<ll> res(n + 1);while(i < n){if(a[i] == 0){i ++; continue;}//统计连续1的个数int j = i;while(j < n && a[j] == 1){j ++;}//统计每种大小的高（或宽）度的的个数for(int len = 1; len <= j - i; len ++){res[len] += j - i - len + 1;        //⚠️  j - i - len + 1 是长度为 len 大小的个数,在长度 为 j - i 的连续1子串中}i = j;}return res;
}int main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("A.txt","r",stdin);int n,m,k;cin >> n >> m >> k;vector<int> a(n);vector<int> b(m);for(auto &x : a)cin >> x;for(auto &y : b)cin >> y;ll ans = 0;//预处理操作auto ha = gao(a);auto wb = gao(b);//遍历每一种 size = k 的矩形for(int i = 1; i <= n; i ++){if(k % i == 0 && k / i <= m){int h = i, w = k / i;ans += ha[h] * wb[w];}}cout << ans << endl;return 0;
}

C. Unusual Competitions（前缀差值）

• 题意：给一个仅由 “（”和 “）”组成的括号序列 例如：“ ) ) ( ( ( ) ) (”，问最少需要需要变换让左右的括号一一对应，这里的变换指的是：选择一段在括号序列的区间 [ l , r ] , 可以把这个区间内的括号，任意交换顺序，但不能改变左右的括号的数量
• 思路：
  • 分析如果我们想把所有的括号匹配，首先的前提就是，在所给的序列中左右括号的数列要相等，若果不想等直接输出-1， 如果先等变换的最小长度为最大长度是，我们选择整个序列进行变换，就一定能够得到答案
  • 对于这一看答案上：引入了一个前缀的东西，这个“前缀差值东西”: pre[ i ] 是 从 1 ～ i 位置 左括号的数量 - 右括号的数量 的差值，这个差值可以模仿 前缀和来理解，我在结合这个图理解一下就行了
  • 其实除了 上面的方法我们能把一些东西都明白，就容易了 其实我们可以 从 左到右 对这个序列，进行考虑，如果我们一开始 遇到的是一个匹配好的序列，那么我可以直接跳过这个序列，对剩下的序列进行讨论，而遇到不配的序列，我们就从左到右找到最短的左右括号数量相同的序列，根据贪心的思想直接变换这个字段就行了（这样得剩下的仍是 左右括号数量相同），反过来想如果我们 不变换这一段的部分行吗？？

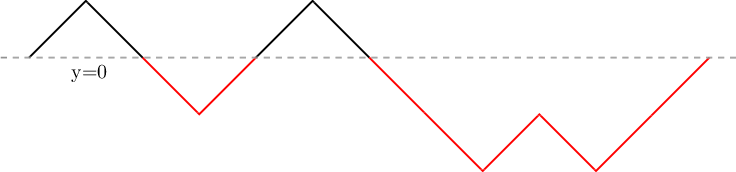
初始序列：Given sequence was ( ) ) ( ( ) ) ) ( ) ( (

变化后的序列：After reshuffling 2 segments of total length 8, we can get a right bracketed sequence: ( ) ( ) ( ( ( ) ( ) )

• 代码

#include<iostream>
#include<vector>
using namespace std;const int Len = 1e6 + 5;
char ar[Len];
int pre[Len];       //pre 数组是前缀差额, pre[i]  的值为：在前i个字符中, 右括号‘（’ 的数量 - 左括号的数量‘）’int main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);//freopen("A.txt","r",stdin);int n;cin >> n;char ch;int op = 0, cl = 0;int last = 0;int ans = 0;for(int i = 1; i <= n; i ++){cin >> ch;if(ch == '('){op ++;pre[i] = pre[i - 1] + 1;}else{cl ++;pre[i] = pre[i - 1] - 1;}if(pre[i] == 0){if(pre[i - 1] < 0){ans += i - last; }last = i;}}if(op == cl)cout << ans << endl;elsecout << -1 << endl;return 0;
}

• 收获：知道可以用前缀差值这个东西，可以用来处理对序列的操作