本文主要是介绍NewOJ Week 8题解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
比赛链接:http://oj.ecustacm.cn/contest.php?cid=1022
题目总览
| 题目 | TAG | 难度 | 来源 | 补题链接 |
|---|---|---|---|---|
| 猜数字 | 概率计算 | ☆ | C o d e C h e f CodeChef CodeChef | http://oj.ecustacm.cn/problem.php?id=1826 |
| 升降数字 | 贪心 | ☆☆ | P A C N W 2021 PACNW \ 2021 PACNW 2021 | http://oj.ecustacm.cn/problem.php?id=1827 |
| 黑白配 | 期望 D P DP DP、状态压缩 D P DP DP | ☆☆☆☆ | P A C N W 2021 PACNW \ 2021 PACNW 2021 | http://oj.ecustacm.cn/problem.php?id=1828 |
| 最短缺失子序列 | 思维题、贪心、字符匹配 | ☆☆☆☆ | P A C N W 2021 PACNW \ 2021 PACNW 2021 | http://oj.ecustacm.cn/problem.php?id=1829 |
| 房间划分 | 计算几何、三角形面积 | ☆☆☆ | P A C N W 2021 PACNW \ 2021 PACNW 2021 | http://oj.ecustacm.cn/problem.php?id=1830 |
A 猜数字
题意: A l i c e Alice Alice从数字 [ 1 , N ] [1,N] [1,N]中随机选择一个整数作为 x x x, B o b Bob Bob从数字 [ 1 , M ] [1,M] [1,M]中随机选择一个整数作为 y y y。求 x + y x+y x+y等于奇数的概率是多少?
Tag: 概率计算
难度: ☆
来源: C o d e C h e f CodeChef CodeChef
思路: 总共存在 N M NM NM种选择情况。要求和为奇数,要么 x x x奇 y y y偶,或者 x x x偶 y y y奇。
可以直接分类讨论求出 [ 1 , N ] [1,N] [1,N]的奇数、偶数数量,也可以根据数学规律计算出 [ 1 , N ] [1,N] [1,N]中的奇数个数为 ⌊ N + 1 2 ⌋ \lfloor \frac{N+1}{2}\rfloor ⌊2N+1⌋,偶数个数为 ⌊ N 2 ⌋ \lfloor \frac{N}{2} \rfloor ⌊2N⌋。
最终要对答案进行约分,求出最大公因数即可。
#include<bits/stdc++.h>
using namespace std;
int main()
{int T;cin >> T;while(T--){long long n, m;cin >> n >> m;//奇数:(n + 1) / 2,偶数n / 2long long p = ((n + 1) / 2) * (m / 2) + ((m + 1) / 2) * (n / 2);long long q = n * m;long long g = __gcd(p, q);cout<<p/g<<"/"<<q/g<<endl;}return 0;
}
B 升降数字
题意: 升降数字:一个数字可以被分成两部分(可能有一部分是空的),第一部分属于非递减,第二部分属于非递增。现在给定数字 n n n,请求出不超过 n n n的最大的升降数字。
Tag: 贪心
难度: ☆☆
来源: P A C N W 2021 PACNW \ 2021 PACNW 2021
思路: 对于给定的数字 n n n,直接从前往后找出最远的满足非递减的部分,然后再接着找出最远的满足非递增部分。
例如数字 12345666544342 12345666544342 12345666544342,首先从前往后找非递减部分: 12345666 12345666 12345666;然后接着找非递增, 123456665443 123456665443 123456665443,后面的部分是不满足的部分。
题目要求第一个是要求比数字 n n n小,第二个是要把后半部分变成非递增。则最优情况是将后面所有非法的全部变成最后一个合法的数字。
上面的例子也就是 12345666544333 12345666544333 12345666544333。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
char s[maxn];
int main()
{int T;scanf("%d", &T);while(T--){scanf("%s", s);int n = strlen(s);int idx = 0;//非递减部分while(s[idx] <= s[idx + 1] && idx + 1 < n)idx++;//非递增部分while(s[idx] >= s[idx + 1] && idx + 1 < n)idx++;//非法部分for(int i = idx; i < n; i++)s[i] = s[idx];printf("%s\n", s);}return 0;
}
C 黑白配
题意: 黑白配是一个经典的游戏,在每一轮中,孩子们将手朝上(白色)或者朝下(黑色)。
如果所有的孩子做出相同的选择,只有一个例外,那么剩下的孩子将会被淘汰。
游戏重复进行,直到只剩下两个孩子停止。
每个孩子有一个固定的概率独立选择是否将手朝上。
给定 n ( ≤ 20 ) n(\le 20) n(≤20)个孩子的概率,请输出游戏期望回合数是多少。
Tag: 期望 D P DP DP、状态压缩 D P DP DP
难度: ☆☆☆☆
来源: P A C N W 2021 PACNW \ 2021 PACNW 2021
思路: 初始状态是 n n n个人都参与游戏,终止状态是参与人数等于 2 2 2个人。由于 n n n很小,用二进制数字 x x x表示 n n n个人的淘汰情况。
例如 x = 3 = ( 111 ) 2 x=3=(111)_2 x=3=(111)2表示1、2、3均未淘汰,而 x = 2 = ( 010 ) 2 x=2=(010)_2 x=2=(010)2则表示 1 1 1、 3 3 3被淘汰。
d p [ x ] dp[x] dp[x]表示状态为 x x x的期望回合数,在此情况下进行一轮游戏,存在两种可能:
- 游戏状态发生改变,即有人淘汰,记概率为 t o t tot tot
- 游戏状态未发生改变,即没有人淘汰,概率为 ( 1 − t o t ) (1-tot) (1−tot)
那么状态 x x x的期望轮次等于:
E [ x ] = t o t ⋅ E [ y ] + ( 1 − t o t ) ⋅ E [ x ] + 1 E[x]=tot \cdot E[y]+(1-tot)\cdot E[x]+1 E[x]=tot⋅E[y]+(1−tot)⋅E[x]+1
上式中的 y y y表示 x x x状态淘汰某个人后变成的状态,实际上可能存在 k k k种转移情况:
E [ x ] = ∑ i = 1 k p y i ⋅ E [ x − 2 y i ] + ( 1 − ∑ i = 1 k p y i ) ⋅ E [ x ] + 1 E[x]=\sum_{i=1}^k p_{y_i}\cdot E[x-2^{y_i}] + \left(1-\sum_{i=1}^kp_{y_i}\right)\cdot E[x]+1 E[x]=i=1∑kpyi⋅E[x−2yi]+(1−i=1∑kpyi)⋅E[x]+1
上式的 ∑ i = 1 k p y i \sum_{i=1}^kp_{y_i} ∑i=1kpyi就等于 t o t tot tot,总共存在 k k k种淘汰情况,其中 k k k表示 x x x中1的个数, x x x的第 y i y_i yi位等于1。
第 y i y_i yi个人淘汰后,状态由 x x x转变成 x − 2 y i x-2^{y_i} x−2yi。
为了求解 E [ x ] E[x] E[x],将 E [ x ] E[x] E[x]放在一边,用 t o t tot tot简化上式:
t o t ⋅ E [ x ] = ∑ i = 1 k p y i ⋅ E [ x − 2 y i ] + 1 tot\cdot E[x] =\sum_{i=1}^k p_{y_i}\cdot E[x-2^{y_i}]+1 tot⋅E[x]=i=1∑kpyi⋅E[x−2yi]+1
这样暴力用二进制枚举求解 E E E数组即可。注意 p y i p_{y_i} pyi表示的是在状态 x x x下第 y i y_i yi个人淘汰的概率,存在两种情况:其他人全白第 y i y_i yi个人黑,或者反过来。
#include<bits/stdc++.h>
using namespace std;
int n;
double p[20];
double dp[(1 << 20) + 10];
//dp[i]表示剩余人数状态为i时的期望轮数inline int bin_count(int x)
{int ans = 0;while(x)++ans, x -= (x & (-x));return ans;
}int main()
{cin >> n;for(int i = 0; i < n; i++)cin >> p[i];for(int x = 0; x < (1 << n); x++){if(bin_count(x) <= 2)continue;//当前状态下所有人出白的概率,出黑的概率double aw = 1.0, ab = 1.0;for(int i = 0; i < n; i++)if(x & (1 << i))aw *= p[i], ab *= (1 - p[i]);//tot表示当前状态x可以转移到其他状态的概率(有人淘汰的概率)double tot = 0.0;for(int i = 0; i < n; i++)if(x & (1 << i)){//pi表示淘汰第i个人的概率double pi = aw / p[i] * (1 - p[i]) + ab / (1 - p[i]) * p[i];dp[x] += pi * dp[x - (1 << i)];tot += pi;}dp[x] = (dp[x] + 1) / tot;}cout<<fixed<<setprecision(12)<<dp[(1 << n) - 1]<<endl;return 0;
}
D 最短缺失子序列
题意:字符串 t t t是字符串 s s s的子序列:字符串 s s s删除 0 0 0个或者多个字符可变成字符 t t t。
字符串 t t t是字符串 s s s的缺失子序列:字符串 t t t不是字符串 s s s的子序列,但是字符串 t t t中出现的字母,均在 s s s中出现过。
字符串 t t t是字符串 s s s的最短缺失子序列:字符串 t t t是字符串 s s s的缺失子序列,同时长度是最短的。
现在给定字符串 s s s,询问 m m m次,每次询问一个字符串 t t t是否为 s s s的最短缺失子序列。
Tag: 思维题、贪心、字符匹配
难度: ☆☆☆☆
来源: P A C N W 2021 PACNW \ 2021 PACNW 2021
思路: 首先最短缺失子序列长度是固定的,因此第一步是求出这个长度。
对于仅由前 c c c个字母组成的字符串 s s s,最短缺失子序列长度是多少呢?
例如仅有前 3 3 3个字母组成的字符串 " a b c c b a " "abccba" "abccba",可以发现在其中长度为1的子序列不是缺失子序列,长度为2的子序列 a a , a b , a c , b a , b b , b c , c a , c b , c c aa,ab,ac,ba,bb,bc,ca,cb,cc aa,ab,ac,ba,bb,bc,ca,cb,cc也不是缺失子序列。
什么情况下长度为 i i i的子序列全都不是缺失子序列?
前 c c c个字母恰好出现 i i i次?更确切的说应该是存在 i i i段,每段包含前 c c c个字母至少 1 1 1次。
例如上述字符串 a b c c b a abccba abccba,可以分成两端 a b c abc abc、 c b a cba cba,正好 a b c abc abc都出现 1 1 1次,这样长度为 2 2 2的子序列肯定都可以构造出,只要每段选一个字母即可。
再例如字符串 a b c c a b c c a abccabcca abccabcca,最多分成两部分 a b c abc abc、 c a b c c a cabcca cabcca,每部分 a b c abc abc都至少出现 1 1 1次,说明最短缺失子序列长度为 3 3 3。
所以给定字符串 s s s,直接贪心从左往右每次从 l l l开始找一个最靠左的端点 r r r,使得 [ l , r ] [l,r] [l,r]满足前 c c c个字母至少出现1次。找出的段数+1就是最短缺失子序列长度。
求出长度之后,对于每次询问 t t t只需要判断两件事:
1、字符串 t t t的长度是否等于最短缺失子序列
2、 t t t是否不是 s s s的子序列。
判断字符串 t t t是否不是 s s s的子序列,可以利用数组 N e x t [ i ] [ j ] Next[i][j] Next[i][j]在线性时间内判断。
N e x t [ i ] [ j ] Next[i][j] Next[i][j]表示第 i i i个位置之后第 j j j个字母的位置,在输入的时候就可以预处理好。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10;
char v[30], s[maxn], t[maxn];///Next[i][j]表示第i位后字符'A'+j的位置
int Next[maxn][26];
///Next[0]存储每个字符第一次出现的位置int main()
{scanf("%s", v + 1);scanf("%s", s + 1);int vlen = strlen(v + 1), slen = strlen(s + 1);//求最短缺失子序列长度lenint K = 0, len = 1;for(int i = 1; i <= vlen; i++)K |= (1 << (v[i] - 'A'));int tK = 0;for(int i = 1; i <= slen; i++){tK |= (1 << (s[i] - 'A'));if(tK == K)len++, tK = 0;//对于字符s[i],往前暴力更新Next数组for(int j = i - 1; j >= 0; j--){Next[j][s[i] - 'A'] = i;//直到找到上一个s[i]停止if(s[j] == s[i])break;}}int n;scanf("%d", &n);while(n--){scanf("%s", t + 1);int tlen = strlen(t + 1);int ok = 0;if(tlen == len)//保证最短{int pos = 0;for(int i = 1; i <= tlen; i++){pos = Next[pos][t[i] - 'A'];if(!pos)break;}//pos等于0说明是无法匹配的//此时为缺失子序列ok = (pos == 0);}printf("%d\n", ok);}return 0;
}
E 房间划分
题意: 给定一个凸多边形房间,现在需要将房间划分成等面积的两部分。
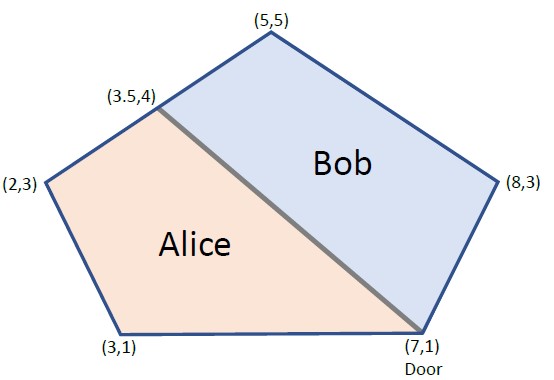
房间只有一个门,可以视为一个顶点,需要沿着直线将房间划分成两部分。
直线的一端必须是门,另一端必须是墙角或者墙壁。
如下图所示,最终需要求解出直线另一端点的坐标。
Tag: 计算几何、三角形面积
难度: ☆☆☆
来源: P A C N W 2021 PACNW \ 2021 PACNW 2021
思路: 题目相当于给一个凸多边形,找一条直线使得面积平分。直线的一点在第一个端点上,请求出另一个在凸多边形边上的端点。
利用三角形面积公式可以求出凸多边形面积 S = ∑ i = 2 n − 1 S Δ ( p [ 1 ] , p [ i ] , p [ i + 1 ] ) S=\sum_{i=2}^{n-1}S_\Delta(p[1],p[i],p[i+1]) S=∑i=2n−1SΔ(p[1],p[i],p[i+1])。
求出 S S S后,求第几个三角形加入后,面积恰好从小于 S 2 \frac{S}{2} 2S变成大于等于 S 2 \frac{S}{2} 2S。
假设 Δ ( p [ 1 ] , p [ i ] , p [ i + 1 ] ) \Delta(p[1],p[i],p[i+1]) Δ(p[1],p[i],p[i+1])后恰好满足上述条件,记加入前面积为 S 1 S_1 S1,加入后面积为 S 2 S_2 S2,则在线段 [ p [ i ] , p [ i + 1 ] ] [p[i],p[i+1]] [p[i],p[i+1]]等比例找一个点 x x x满足:
∣ ∣ x − p [ i ] ∣ ∣ ∣ ∣ p [ i + 1 ] − p [ i ] ∣ ∣ = S 2 − S 1 S 2 − S 1 \frac{||x-p[i]||}{||p[i+1]-p[i]||} = \frac{\frac{S}{2}-S_1}{S_2-S_1} ∣∣p[i+1]−p[i]∣∣∣∣x−p[i]∣∣=S2−S12S−S1
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
typedef long long ll;
int n;
struct Point
{double x, y;Point(){}Point(double x, double y):x(x), y(y){}void input(){scanf("%lf%lf", &x, &y);}Point operator -(const Point& a)const{return Point(x - a.x, y - a.y);}Point operator +(const Point& a)const{return Point(x + a.x, y + a.y);}Point operator *(double p)const{return Point(x * p, y * p);}
}node[maxn];
typedef Point Vector;
//叉积
inline double Cross(Vector A, Vector B){return A.x*B.y - A.y*B.x;
}
//三角形面积
inline double Area(Point A, Point B, Point C){return 0.5 * Cross(B-A, C-A);
}int main()
{scanf("%d", &n);for(int i = 1; i <= n; i++)node[i].input();double half_area = 0;for(int i = 2; i <= n - 1; i++)half_area += Area(node[1], node[i], node[i + 1]);half_area *= 0.5;double now_area = 0;for(int i = 2; i <= n - 1; i++){double next_area = now_area + Area(node[1], node[i], node[i + 1]);if(now_area <= half_area && next_area >= half_area){//cout<<i<<" "<<now_area<<" "<<half_area<<" "<<next_area<<endl;//AB = AM + MB//(half_area - now_area) : (next_area - now_area) = AM : ABdouble p = (half_area - now_area) / (next_area - now_area);Point delta = (node[i + 1] - node[i]) * p;Point ans = node[i] + delta;printf("%.9f %.9f\n", ans.x, ans.y);break;}now_area = next_area;}return 0;
}
这篇关于NewOJ Week 8题解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







