【滑动窗口】“正难则反法” 解决最小操作数的问题

本文主要是介绍【滑动窗口】“正难则反法” 解决最小操作数的问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

Problem: 1658. 将 x 减到 0 的最小操作数

文章目录

题目解析
算法原理分析
Code
复杂度

题目解析

首先我们来解读一下本题的题目含义

题目会给到我们一个整数数组和一个整数x，我们可以从左侧，也可以从右侧去减，只要让这个x最终减到【0】即可。
不过呢既然可以从左边也可以从右边减的话就一定存在多种方案，我们所需要的话是操作次数最少的那次，看到下面我列出来的两种情况，很明显第二种方法 从右侧删去两个数据更加优的

算法原理分析

接下去我们来介绍一下本题的算法原理

通过刚才的分析相信很多小伙伴认为本题的题目意思并不是很难理解，但是呢想找到对应的解决方案还是比较困难的，在这里的话教大家一种方法叫做 “正难则反法"
题目中要我们去找的是左右两侧的 最小操作数，但是呢这并不好计算，于是我们可以换个思路，将左侧的数据看做是一个整体，记为a；将右侧的数据看做是一个整体，记为b；那么我们可以得出a + b = x
既然左右两侧的是x的话，那么中间的一段就是sum - x。而且既然两边需要最短的话，中间我们要找的就是【最长的那一段】

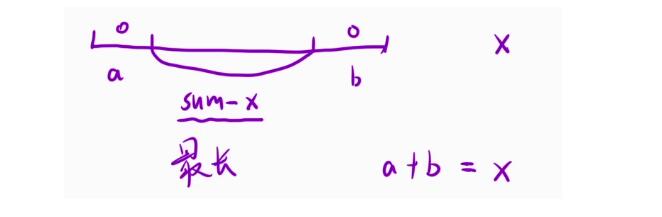
因此经过上面的步步分析，我们便将题目的意思转换为了去找 数组里面最长子数组的长度，而且它们的和即为sum - x的结果。不过最后我们要返回的结果可不是这个长度len，而是n - len

本题我们还是考虑使用滑动窗口来进行求解，因为滑动窗口本身就是基于【双指针】的，所以读者在看此文的时候可以先看看我『双指针』的专栏题解
我们的right指针还是一样作为向后遍历并进行计数累加的指针，当其没有达到target的时候就继续去作累加的操作，这相当于是【进窗口】的操作。当其到中间这个点的时候此时sum的值只会是 大于或者等于target的；
当sum == target 的时候呢便去做更新长度的操作。当sum > target的时候我们就要去考虑【出窗口】的操作，将左侧的left指针所指向的内容从我们所累加的和中减去，然后还需要执行left++让其继续后移

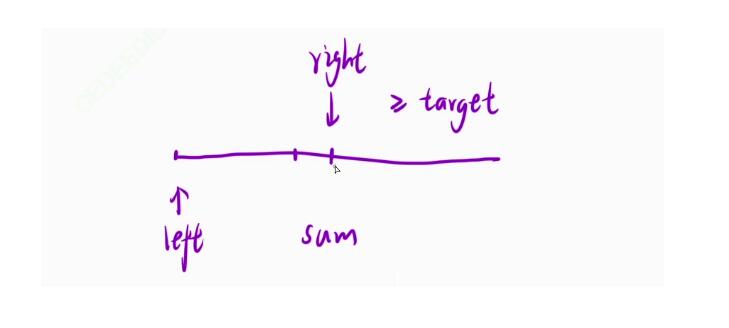
那有同学问：right还需要回来吗，还是持续后移呢？

我们来探讨一下这个问题，因为在中间这个点的时候sum >= target，那从最左侧到这个点前面一个点的总和是< target的，那如果我们使用暴力解法的话在left向后移动的时候，此时如果right再回来的话，其实是没有必要了，因为left++执行了出窗口的操作后，这个sum就更为小了，此时让right--再左移的话只会更小
所以我们的和这个right是不需要回来的，它只会在那个== target的位置或者是> target的位置

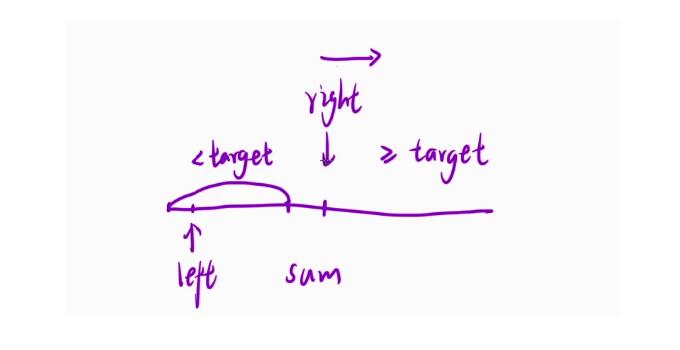
💬 最后的代码详解我们马上来看看看【code】部分，不过读者可以根据算法原理的解读自己试着写写看

Code

对于代码而言的话读者基本上就是根据我们前面所描述的去进行书写即可，还有一些细节地方需要注意

题目中给到的提示这一块，即数组里面所有的数据都是大于1的，那么我们数组中找这个target的时候是不会出现负数这种情况的，所以若是遇到这种情况的，我们直接return -1即可

以下是整体的代码详解：


class Solution {
public:int minOperations(vector<int>& nums, int x) {int n = nums.size();int sum1 = 0;    // 用于先行求出整个数组的和int sum2 = 0;    // 用于遍历数组时的累加int ret = -1;for(int a : nums)   sum1 += a; int target = sum1 - x;      // 减去两端的数据后中间的和// 处理细节：数组中不会存在负数, 若存在的话则表示找不到if(target < 0)  return -1;for(int left = 0, right = 0; right < n; ++right){// 1.进窗口sum2 += nums[right];// 累加和超过target则开始出窗口while(sum2 > target){// 2.出窗口sum2 -= nums[left++]; }// 3.更新结果if(sum2 == target)ret = max(ret, right - left + 1);}if(ret == -1)   return ret;elsereturn n - ret;    // 减去最长的子串即为最小操作数}
};

下面则是执行的结果：