2106. 摘水果（每日一难phase-day22）

本文主要是介绍2106. 摘水果（每日一难phase-day22），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2106. 摘水果

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列，每个 positioni 互不相同。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择向左或者向右走。在 x 轴上每移动 一个单位 ，就记作一步。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：
在这里插入图片描述

输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：最佳路线为：

向右移动到位置 6 ，摘到 3 个水果
向右移动到位置 8 ，摘到 6 个水果移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：
在这里插入图片描述

输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k =4
输出：14
解释：可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。最佳路线为：

在初始位置 5 ，摘到 7 个水果
向左移动到位置 4 ，摘到 1 个水果
向右移动到位置 6 ，摘到 2 个水果
向右移动到位置 7 ，摘到 4 个水果移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：
在这里插入图片描述

输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：最多可以移动 k= 2 步，无法到达任一有水果的地方

提示：

1 <= fruits.length <= 1e5
fruits[i].length == 2
0 <= startPos, positioni <= 2 * 1e5
对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0开始计数）
1 <= amounti <= 1e4
0 <= k <= 2 * 1e5

解析：

双指针滑动窗口
分为三种情况，右指针在左侧，左指针在右侧，左指针左，右指针右
前两种情况需要保证：（r-l）<=k && (r-l)+min(abs(s-l),abs(s-r))<=k
具体代表什么意思呢？r-l<=k表示窗口区间小于k，（r-l）<=k && (r-l)+min(abs(s-l),abs(s-r))<=k表示最远处离startPos距离小于等于k。
可以看出 &&右式包含左式（同大取大），因此可以写成：
(r-l)+min(abs(s-l),abs(s-r))<=k
再看第三种情况：左右指针分别位于两侧
需要保证：（r-l）+min(s-l,r-s)<=k

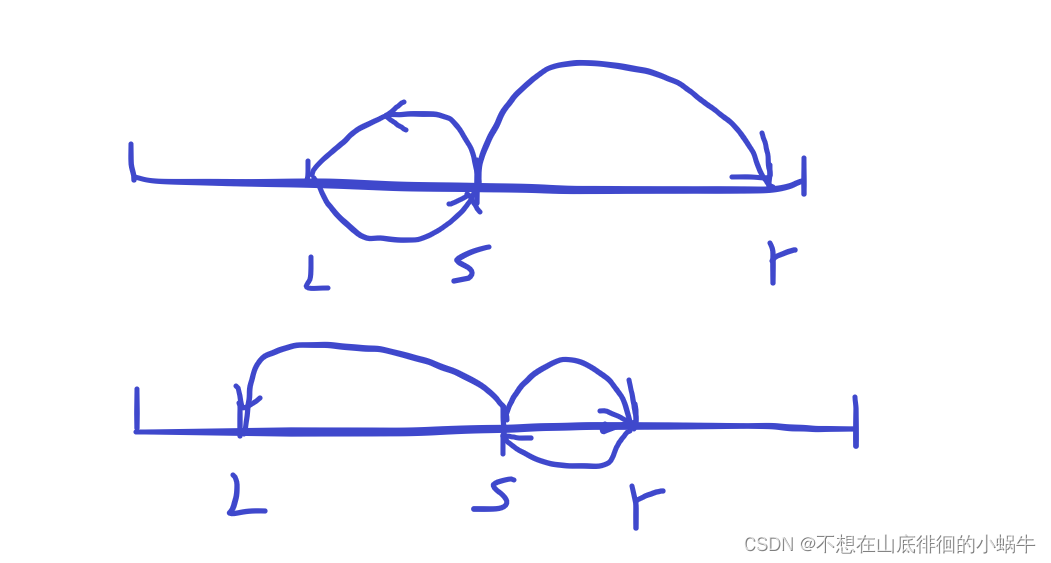
可以看出两式可以合并为：(r-l)+min(abs(s-l),abs(s-r))<=k，因此满足该种情况右指针右移，不满足左指针左移即可。

代码：

class Solution {
public:int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {int n=fruits.size();int l=0,r=0;int res=0,tmp=0;while(r<n){int rdiff = abs(startPos-fruits[r][0]);while(l<=r&&fruits[r][0]-fruits[l][0]+min(abs(startPos-fruits[l][0]), rdiff)>k){tmp-=fruits[l][1];l++;}// 正确状态得到结果tmp+=fruits[r][1];res=max(res,tmp);r++;        }return res;}
};