Genetic Algorithm遗传算法学习

本文主要是介绍Genetic Algorithm遗传算法学习，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考资料：http://blog.csdn.net/b2b160/article/details/4680853/#comments(冒昧的用了链接下的几张图)
百度百科：http://baike.baidu.com/link?url=FcwTBx_yPcD5DDEnN1FqvTkG4QNllkB7Yis6qFOL65wpn6EdT5LXFxUCmv4JlUfV3LUPHQGdYbGj8kHVs3GuaK

算法介绍

遗传算法是模拟达尔文生物进化论的自然选择和遗传学进化机理的计算模型。运用到了生物学中“适者生存，优胜劣汰”的原理。在每一次的进化过程中，把拥有更好环境适应性的基因传给下一代，直到最后的个体满足特定的条件，代表进化的结束，GA(后面都以GA代称为遗传算法的意思)算法是一种利用生物进化理论来搜索最优解的一种算法。

算法原理

算法的基本框架

了解算法的基本框架是理解整个算法的基础，算法的框架包含编码、适应度函数、初始群体的选择。先假设本例子的目标函数如下,求出他的最大值

f(x) = x1 * x1 + x2 * x2; 1<= x1 <=7,1<= x2<=7

1、适应度函数。适应度函数是用来计算个体的适应值计算，顾名思义，适应值越高的个体，环境适应性越好，自然就要有更多的机会把自己的基因传给下一代，所以，其实适应度函数在这里起着一个过滤条件的作用。在本例子，目标函数总为非负值，并且以函数最大化为优化目标，所以可以将函数的值作为适应值。

2、编码。编码指的是将个体的信息表示成编码的字符串形式。如果个体变量时数字的形式，可以转为二进制的方式。

算法的群体选择过程

这个过程是遗传算法的核心过程，在里面分为了3个小的步骤，选择，交叉，变异。

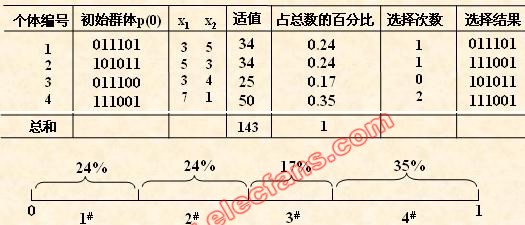
1、初始个体的选择过程。就是挑选哪些个体作为即将产生下一代的个体呢。过程如下：

(1).利用适值函数，计算每个个体的适值，计算每个个体的适值占总和的百分比。

(2).根据百分比为每个个体划定一定的所属区间。

(3).产生一个[0, 1]的小数，判断这个小数点落在哪个个体的区间内，就表明要选出这个个体。这里其实就已经蕴含着把高适值的个体优先传入下一代，因为适值高，有更高的几率小数是落在自己的区间内的。

用图示范的形式表现如下：

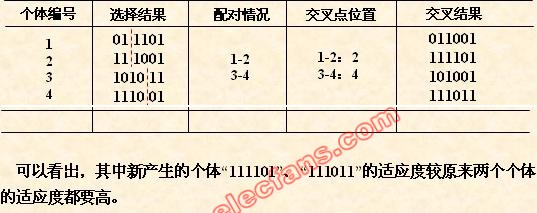
2、交叉运算。个体的交叉运算过程的步骤细节如下：

(1).首先对于上个选择步骤选择来的个体进行随机的两两配对。

(2).取出其中配对的一对个体，随机设定一个交叉点，2个个体的编码的交叉点后的编码值进行对调，生成新的2个个体编码。

(3).所有的配对的个体都执行步骤(2)操作，最后加入到一个结果集合中。

交叉运算的方式又很多，上面用的方法是其中比较常用的单点交叉方式。

用图示范的形式表现如下：

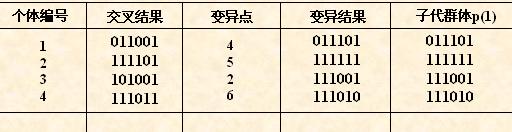
3.变异运算。变异运算过程的步骤细节如下：

(1).遍历从交叉运算所得结果的结果集，取出集中一个个体编码,准备做变异操作

(2).产生随机的一个变异点位置。所选个体的变异点位置的值做变异操作，将他的值取为反向的值。

(3).将所有的交叉运算所得的结果集中的元素都执行步骤(2)操作。

用图示范的形式如下：

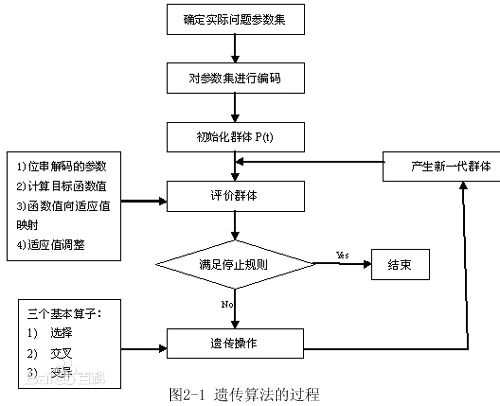
整个遗传算法的原理过程，用一个流程图的表现形式如下：

算法代码实现

算法代码的测试用例正如算法原理所举的一样，遗传进化的阈值条件为：个体中产生了使目标函数最大化值的个体，就是基因为111111。

GATool.java:

[java] view plain copy print ?  
 packageGA; 
  
 importjava.util.ArrayList; 
 importjava.util.Random; 
  
 /** 
 *遗传算法工具类 
 * 
 *@authorlyq 
 * 
 */ 
 publicclassGATool{ 
 //变量最小值 
 privateintminNum; 
 //变量最大值 
 privateintmaxNum; 
 //单个变量的编码位数 
 privateintcodeNum; 
 //初始种群的数量 
 privateintinitSetsNum; 
 //随机数生成器 
 privateRandomrandom; 
 //初始群体 
 privateArrayList<int[]>initSets; 
  
 publicGATool(intminNum,intmaxNum,intinitSetsNum){ 
 this.minNum=minNum; 
 this.maxNum=maxNum; 
 this.initSetsNum=initSetsNum; 
  
 this.random=newRandom(); 
 produceInitSets(); 
 } 
  
 /** 
 *产生初始化群体 
 */ 
 privatevoidproduceInitSets(){ 
 this.codeNum=0; 
 intnum=maxNum; 
 int[]array; 
  
 initSets=newArrayList<>(); 
  
 //确定编码位数 
 while(num!=0){ 
 codeNum++; 
 num/=2; 
 } 
  
 for(inti=0;i<initSetsNum;i++){ 
 array=produceInitCode(); 
 initSets.add(array); 
 } 
 } 
  
 /** 
 *产生初始个体的编码 
 * 
 *@return 
 */ 
 privateint[]produceInitCode(){ 
 intnum=0; 
 intnum2=0; 
 int[]tempArray; 
 int[]array1; 
 int[]array2; 
  
 tempArray=newint[2*codeNum]; 
 array1=newint[codeNum]; 
 array2=newint[codeNum]; 
  
 num=0; 
 while(num<minNum||num>maxNum){ 
 num=random.nextInt(maxNum)+1; 
 } 
 numToBinaryArray(array1,num); 
  
 while(num2<minNum||num2>maxNum){ 
 num2=random.nextInt(maxNum)+1; 
 } 
 numToBinaryArray(array2,num2); 
  
 //组成总的编码 
 for(inti=0,k=0;i<tempArray.length;i++,k++){ 
 if(k<codeNum){ 
 tempArray[i]=array1[k]; 
 }else{ 
 tempArray[i]=array2[k-codeNum]; 
 } 
 } 
  
 returntempArray; 
 } 
  
 /** 
 *选择操作，把适值较高的个体优先遗传到下一代 
 * 
 *@paraminitCodes 
 *初始个体编码 
 *@return 
 */ 
 privateArrayList<int[]>selectOperate(ArrayList<int[]>initCodes){ 
 doublerandomNum=0; 
 doublesumAdaptiveValue=0; 
 ArrayList<int[]>resultCodes=newArrayList<>(); 
 double[]adaptiveValue=newdouble[initSetsNum]; 
  
 for(inti=0;i<initSetsNum;i++){ 
 adaptiveValue[i]=calCodeAdaptiveValue(initCodes.get(i)); 
 sumAdaptiveValue+=adaptiveValue[i]; 
 } 
  
 //转成概率的形式，做归一化操作 
 for(inti=0;i<initSetsNum;i++){ 
 adaptiveValue[i]=adaptiveValue[i]/sumAdaptiveValue; 
 } 
  
 for(inti=0;i<initSetsNum;i++){ 
 randomNum=random.nextInt(100)+1; 
 randomNum=randomNum/100; 
  
 sumAdaptiveValue=0; 
 //确定区间 
 for(intj=0;j<initSetsNum;j++){ 
 if(randomNum>sumAdaptiveValue 
 &&randomNum<=sumAdaptiveValue+adaptiveValue[j]){ 
 //采用拷贝的方式避免引用重复 
 resultCodes.add(initCodes.get(j).clone()); 
 break; 
 }else{ 
 sumAdaptiveValue+=adaptiveValue[j]; 
 } 
 } 
 } 
  
 returnresultCodes; 
 } 
  
 /** 
 *交叉运算 
 * 
 *@paramselectedCodes 
 *上步骤的选择后的编码 
 *@return 
 */ 
 privateArrayList<int[]>crossOperate(ArrayList<int[]>selectedCodes){ 
 intrandomNum=0; 
 //交叉点 
 intcrossPoint=0; 
 ArrayList<int[]>resultCodes=newArrayList<>(); 
 //随机编码队列，进行随机交叉配对 
 ArrayList<int[]>randomCodeSeqs=newArrayList<>(); 
  
 //进行随机排序 
 while(selectedCodes.size()>0){ 
 randomNum=random.nextInt(selectedCodes.size()); 
  
 randomCodeSeqs.add(selectedCodes.get(randomNum)); 
 selectedCodes.remove(randomNum); 
 } 
  
 inttemp=0; 
 int[]array1; 
 int[]array2; 
 //进行两两交叉运算 
 for(inti=1;i<randomCodeSeqs.size();i++){ 
 if(i%2==1){ 
 array1=randomCodeSeqs.get(i-1); 
 array2=randomCodeSeqs.get(i); 
 crossPoint=random.nextInt(2*codeNum-1)+1; 
  
 //进行交叉点位置后的编码调换 
 for(intj=0;j<2*codeNum;j++){ 
 if(j>=crossPoint){ 
 temp=array1[j]; 
 array1[j]=array2[j]; 
 array2[j]=temp; 
 } 
 } 
  
 //加入到交叉运算结果中 
 resultCodes.add(array1); 
 resultCodes.add(array2); 
 } 
 } 
  
 returnresultCodes; 
 } 
  
 /** 
 *变异操作 
 * 
 *@paramcrossCodes 
 *交叉运算后的结果 
 *@return 
 */ 
 privateArrayList<int[]>variationOperate(ArrayList<int[]>crossCodes){ 
 //变异点 
 intvariationPoint=0; 
 ArrayList<int[]>resultCodes=newArrayList<>(); 
  
 for(int[]array:crossCodes){ 
 variationPoint=random.nextInt(codeNum*2); 
  
 for(inti=0;i<array.length;i++){ 
 //变异点进行变异 
 if(i==variationPoint){ 
 array[i]=(array[i]==0?1:0); 
 break; 
 } 
 } 
  
 resultCodes.add(array); 
 } 
  
 returnresultCodes; 
 } 
  
 /** 
 *数字转为二进制形式 
 * 
 *@parambinaryArray 
 *转化后的二进制数组形式 
 *@paramnum 
 *待转化数字 
 */ 
 privatevoidnumToBinaryArray(int[]binaryArray,intnum){ 
 intindex=0; 
 inttemp=0; 
 while(num!=0){ 
 binaryArray[index]=num%2; 
 index++; 
 num/=2; 
 } 
  
 //进行数组前和尾部的调换 
 for(inti=0;i<binaryArray.length/2;i++){ 
 temp=binaryArray[i]; 
 binaryArray[i]=binaryArray[binaryArray.length-1-i]; 
 binaryArray[binaryArray.length-1-i]=temp; 
 } 
 } 
  
 /** 
 *二进制数组转化为数字 
 * 
 *@parambinaryArray 
 *待转化二进制数组 
 */ 
 privateintbinaryArrayToNum(int[]binaryArray){ 
 intresult=0; 
  
 for(inti=binaryArray.length-1,k=0;i>=0;i--,k++){ 
 if(binaryArray[i]==1){ 
 result+=Math.pow(2,k); 
 } 
 } 
  
 returnresult; 
 } 
  
 /** 
 *计算个体编码的适值 
 * 
 *@paramcodeArray 
 */ 
 privateintcalCodeAdaptiveValue(int[]codeArray){ 
 intresult=0; 
 intx1=0; 
 intx2=0; 
 int[]array1=newint[codeNum]; 
 int[]array2=newint[codeNum]; 
  
 for(inti=0,k=0;i<codeArray.length;i++,k++){ 
 if(k<codeNum){ 
 array1[k]=codeArray[i]; 
 }else{ 
 array2[k-codeNum]=codeArray[i]; 
 } 
 } 
  
 //进行适值的叠加 
 x1=binaryArrayToNum(array1); 
 x2=binaryArrayToNum(array2); 
 result=x1*x1+x2*x2; 
  
 returnresult; 
 } 
  
 /** 
 *进行遗传算法计算 
 */ 
 publicvoidgeneticCal(){ 
 //最大适值 
 intmaxFitness; 
 //迭代遗传次数 
 intloopCount=0; 
 booleancanExit=false; 
 ArrayList<int[]>initCodes; 
 ArrayList<int[]>selectedCodes; 
 ArrayList<int[]>crossedCodes; 
 ArrayList<int[]>variationCodes; 
  
 int[]maxCode=newint[2*codeNum]; 
 //计算最大适值 
 for(inti=0;i<2*codeNum;i++){ 
 maxCode[i]=1; 
 } 
 maxFitness=calCodeAdaptiveValue(maxCode); 
  
 initCodes=initSets; 
 while(true){ 
 for(int[]array:initCodes){ 
 //遗传迭代的终止条件为存在编码达到最大适值 
 if(maxFitness==calCodeAdaptiveValue(array)){ 
 canExit=true; 
 break; 
 } 
 } 
  
 if(canExit){ 
 break; 
 } 
  
 selectedCodes=selectOperate(initCodes); 
 crossedCodes=crossOperate(selectedCodes); 
 variationCodes=variationOperate(crossedCodes); 
 initCodes=variationCodes; 
  
 loopCount++; 
 } 
  
 System.out.println("总共遗传进化了"+loopCount+"次"); 
 printFinalCodes(initCodes); 
 } 
  
 /** 
 *输出最后的编码集 
 * 
 *@paramfinalCodes 
 *最后的结果编码 
 */ 
 privatevoidprintFinalCodes(ArrayList<int[]>finalCodes){ 
 intj=0; 
  
 for(int[]array:finalCodes){ 
 System.out.print("个体"+(j+1)+":"); 
 for(inti=0;i<array.length;i++){ 
 System.out.print(array[i]); 
 } 
 System.out.println(); 
 j++; 
 } 
 } 
  
 } 

算法调用类Client.java：

[java] view plain copy print ?  
 packageGA; 
  
 /** 
 *Genetic遗传算法测试类 
 *@authorlyq 
 * 
 */ 
 publicclassClient{ 
 publicstaticvoidmain(String[]args){ 
 //变量最小值和最大值 
 intminNum=1; 
 intmaxNum=7; 
 //初始群体规模 
 intinitSetsNum=4; 
  
 GATooltool=newGATool(minNum,maxNum,initSetsNum); 
 tool.geneticCal(); 
 } 
 } 

算法多次测试的输出结果：

测试1：

[java] view plain copy print ?  
 总共遗传进化了0次 
 个体1:111001 
 个体2:101010 
 个体3:101110 
 个体4:111111 

测试2：

[java] view plain copy print ?  
 总共遗传进化了1次 
 个体1:101101 
 个体2:111111 
 个体3:100111 
 个体4:100111 

测试3：

[java] view plain copy print ?  
 总共遗传进化了14次 
 个体1:110101 
 个体2:111111 
 个体3:110101 
 个体4:110011 

算法结果分析

可以看到，遗传进化的循环次数还是存在着不确定定性的，原因在于测试的个体数太少，如果个体数比较多的话，几轮就可以出现111111这样的个体编码组了。从结果可以看出，总的还是能够向1多的方向发展的。

说说我对遗传算法的理解

通过实现了GA算法，觉得这有点集成算法的味道，因为这其实用到了跨学科的知识，用生物进化理论的知识，去作为一个搜索最优解的解决方案，而且算法本身理解和实现也不是特别的难。

这篇关于Genetic Algorithm遗传算法学习的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

Genetic Algorithm遗传算法学习

算法介绍

算法原理

算法的基本框架

算法的群体选择过程

算法代码实现

算法结果分析

说说我对遗传算法的理解

相关文章

HarmonyOS学习(七)——UI（五）常用布局总结

Ilya-AI分享的他在OpenAI学习到的15个提示工程技巧

【前端学习】AntV G6-08 深入图形与图形分组、自定义节点、节点动画（下）

学习hash总结

零基础学习Redis(10) -- zset类型命令使用

【机器学习】高斯过程的基本概念和应用领域以及在python中的实例

【学习笔记】陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

线性代数|机器学习-P36在图中找聚类

Node.js学习记录（二）