NOIP2017列队

Sylvia 是一个热爱学习的女♂孩子。
前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。
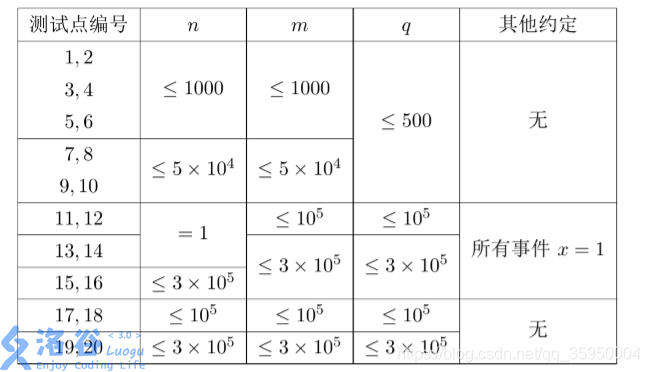
Sylvia 所在的方阵中有名学生，方阵的行数为 n，列数为 m。
为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 1 到 编上了号码（参见后面的样例）。即：初始时，第 i行第 j列 的学生的编号是。
然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 q q件这样的离队事件。每一次离队事件可以用数对(x,y) (1 \le x \le n, 1 \le y \le m)描述，表示第 x行第 y列的学生离队。
在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达 这样的两条指令：
向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 x 行第 m列。
向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 n行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 n 行 第 m 列一个空位，这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学 的编号是多少。
注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后 方阵中同学的编号可能是乱序的。
输入
输入共 q+1行。
第 1 行包含 3 个用空格分隔的正整数 n, m, q，表示方阵大小是 n 行 m 列，一共发 生了 q 次事件。
接下来 q行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x, y用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 x行第 y列。
输出
按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学 生的编号。

这个题首先是动态开点线段树的模板题。
动态开点线段树用来维护有几个人被删掉，快速求出当前这行（列）的第k个人是谁。
然后就很板了啊；
AC Code（写了70行算很菜的了）:

#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
#include<vector>
#define maxn 300005
#define maxm 300005*20
#define LL long long
using namespace std;int n,m,q,len;int tot,lc[maxm],rc[maxm],cut[maxm];
int rt[maxn];
vector<LL>item[maxn];void get(int &res){char ch;while(!isdigit(ch=getchar()));for(res=ch-'0';isdigit(ch=getchar());res=res*10+ch-'0');
}int New()
{++tot;cut[tot]=lc[tot]=rc[tot]=0;return tot;
}void Insert(int &now,int l,int r,int pos)
{if(!now)now=New();cut[now]++;if(l==r) return;int mid=(l+r)>>1;if(pos<=mid) Insert(lc[now],l,mid,pos);else Insert(rc[now],mid+1,r,pos);
}int Query(int now,int l,int r,int pos)
{if(l==r) return l;int mid=(l+r)>>1,siz=mid-l+1-cut[lc[now]];if(siz>=pos) return Query(lc[now],l,mid,pos);else return Query(rc[now],mid+1,r,pos-siz);
}LL Delrow(int u,LL suc)
{int tmp;Insert(rt[n+1],1,len,tmp=Query(rt[n+1],1,len,u));LL ret=(tmp<=n ? 1ll*tmp*m:item[n+1][tmp-n-1]);item[n+1].push_back(suc==-1?ret:suc);return ret;
}LL Delcol(int u,int v)
{int tmp;Insert(rt[u],1,len,tmp=Query(rt[u],1,len,v));LL ret=(tmp<m ? 1ll*(u-1)*m+tmp:item[u][tmp-m]);item[u].push_back(Delrow(u,ret));return ret;
}int main(){//freopen("1.in","r",stdin);//freopen("1.out","w",stdout);int u,v;get(n),get(m),get(q);len=max(n+q,m+q);	for(int i=1;i<=q;i++){get(u),get(v);printf("%lld\n",(v==m)?Delrow(u,-1):Delcol(u,v));}
}

但是出题人扬言要卡线段树，放树状数组过。
但树状数组做这个题就有点曲折了。
第一个难点，线段树的二分结构使得我们可以边二分边求前缀和，做到复杂度O(logn),但是树状数组在蒟蒻的眼中一般来说都只能二分套树状数组O(log^2n),这复杂度首先就不对了。
树状数组也是可以O(logn)并且常数更小的完成这个任务的。
如果你学习过zkw线段树，你可以发现树状数组就是一个省了一半空间的线段树加上中序遍历。
实际上还是可以实现的，具体看代码。
第二个难点，树状数组不能动态开点。
但是你会发现，其实我们需要维护的信息，因为我们是惰性删除，我们只需要求实际的位置就可以，而这针对于各行各列都是相对独立的，那么完全没有必要一遍求出答案，每一行分别处理，最后利用最后一列求出答案就行。

AC Code(50行尚可):

#define maxn 300005
#define LL long long
using namespace std;char cb[1<<15],*cs,*ct;
#define getc() (cs==ct&&(ct=(cs=cb)+fread(cb,1,1<<15,stdin),cs==ct)?0:*cs++)
inline void read(int &res){ char ch;for(;!isdigit(ch=getc()););for(res=ch-'0';isdigit(ch=getc());res=res*10+ch-'0'); }int n,m,q;
int siz,tr[maxn*4],x[maxn],y[maxn],ry[maxn];
vector<LL>vec[maxn],qry[maxn];
inline void upd(int now,int val){ for(;now<=siz;now+=now&-now) tr[now]+=val; }
inline int qsum(int now){ int ret = 0;for(;now;now-=now&-now) ret+=tr[now];return ret; }
inline int Find(int x)
{int ret=1,sum=0;for(;;ret<<=1) if((ret<<1)-tr[ret<<1]>=x) break;if(ret-tr[ret] == x) return ret;sum = tr[ret];for(int k=ret>>1;k;k>>=1) if((ret+k)-tr[ret+k]-sum<x) ret+=k,sum+=tr[ret];return ret+1;
}int main()
{read(n),read(m),read(q),siz=max(n,m)+q;for(int i=1;i<=q;i++){read(x[i]),read(y[i]);if(y[i]!=m) qry[x[i]].push_back(i);}for(int i=1,sz;i<=n;i++){sz=qry[i].size();for(int j=0;j<sz;j++)upd(ry[qry[i][j]]=Find(y[qry[i][j]]),1);for(int j=0;j<sz;j++)upd(ry[qry[i][j]],-1);}for(int i=1,row;i<=q;i++){LL ans = 0;row=Find(x[i]),upd(row,1);ans=(row <=n ? 1ll * row * m : vec[n+1][row-n-1]);if(y[i]!=m)vec[x[i]].push_back(ans),ans=(ry[i] <= m-1 ? 1ll * (x[i]-1)*m+ry[i] : vec[x[i]][ry[i]-m]);vec[n+1].push_back(ans);printf("%lld\n",ans);}
}