一度辍学的数学差生，获得今年菲尔兹奖

杨净 丰色 发自 凹非寺
量子位 | 公众号 QbitAI

小时候数学不好、高中辍学当诗人。

后来为生计学做记者，结果在24岁那年偶然听了节菲尔兹奖得主的课，突然就被打通任督二脉，开始学习数学。

这是新晋菲尔兹奖得主许埈珥的传奇经历——进入数学界15年即登上最高领奖台。

△来源：普林斯顿大学

有观点表示，其不可能的程度，相当于一个人18岁拿起网球拍，20岁赢得温网公开赛。

值得一提的是，这也是继丘成桐、陶哲轩、吴宝珠之后又有亚裔科学家获此殊荣。

15年磨一剑

本次获得表彰的原因是他将霍奇理论的思想引入组合学，证明了几大猜想。

包括几何格的Dowling–Wilson猜想、拟阵的Heron–Rota–Welsh猜想、强梅森猜想，还发展了洛伦兹多项式。

其中最知名的工作，就是他开拓了一种全新的思路，解释并证明了Heron–Rota–Welsh猜想（后简称罗塔猜想）。

罗塔猜想于在1971年提出，研究对象为“拟阵”组合对象。

简单来说，以点和线组合成的图为例，给一个图的顶点着色，两个相邻的点颜色不同。在颜色数量指定的情况下，着色的可能性可以由一个特征多项式的方程来计算。

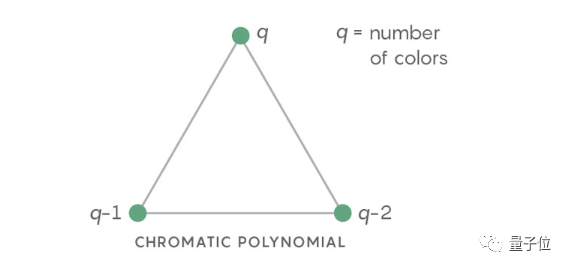
罗塔猜想就预测，任何拟阵的特征多项式的系数总是对数凹的。

值得一提的是，其他两位合作者，一位曾因当厨师放弃学数学，另一位则是资深的摇滚乐爱好者，结果阴差阳错地解决了一个世界级难题。

也正因这项工作他一炮而红， 并很快获得了普林斯顿高等研究院（IAS）长期研究员的头衔。

在他之前，只有三位年轻科学家被授予过该头衔。

其中包含吴宝珠在内的两位科学家，都获得了菲尔兹奖。

于是乎在那时，年仅34岁的他，就已经被认定为菲尔兹奖热门得主。

很难想象，这种大牛般的人生经历会发生在一位半路出家的数学家身上。

事实上，在他数学之旅刚开始之时，即便有菲尔兹奖得主广中平祐（1970年得主）的点拨，但依旧不受学界其他人待见。

在本校读完硕士之后，他申请了十几个美国的博士项目。

无奈研究经历实在是平庸，研究生课程也表现平平，即便有大牛的推荐信，美国高校并不为其所动，传统强校更是拒之千里。最后他也只拿到了一个offer——UIUC。

不过很快，事情来到了转折点。

或许正是因为半路出家，所以从一开始就跟一般数学家的思路就有所不同。

就在第一学期，他就发现可以用奇点理论，即在广中平祐学习到的知识，来证明图论当中诸多性质。

其中就包括一个著名猜想——里德猜想，也可以说是罗塔猜想的特例。两者非常相似，但研究对象不一致。

一个是图，另一个是拟阵。

而在此之前，他甚至都不知道有这个猜想的存在。

他将证明过程po到网上， 结果密歇根大学就邀请他去做报告。

当时一数学家Mircea Mustaţă给予了高度评价，之后也成为了许埈珥的博士生导师。

从某种程度上说，这个报告非常优美和清晰；它一下子就切中了要点。

对于刚开始读研究生的人来说，能做一个如此清楚的报告的并不多见。

会后，密歇根大学当即邀请他转校。于是就在2011年他来到了密歇根读博，当时他来美国还不到两年。

这时候已证明完里德猜想后，他开始转战下一个战场，即里德猜想的进阶版——罗塔猜想。

在密歇根博士毕业后，他曾在IAS、斯坦福大学做过研究员，现在是一名普林斯顿大学的数学教授。

时至今日，他也会在每年暑期回到韩国访学，这个所有一切开始的原点。

大学读了6年

1983年，许埈珥的父母还在美国加州读研究生时生下了他。

2岁时，他们一家回到韩国，爸爸在高丽大学教统计学，妈妈在首尔大学教俄语。

据Quanta Magazine介绍，学校对于许埈珥来说很痛苦，因为他在课堂上无法集中注意力，学不进去东西。

相反，他很喜欢一个人看书，读完了一套生物百科全书的全部10卷，还把家附近的一座山都摸了一个遍。

数学对于它来说，也是个不怎么有意思的东西。父亲给他布置的练习题，他选择直接抄答案。

父亲知道后把答案撕了，他就跑到书店里去抄答案。

小学期间一次考得很砸的数学成绩更是让他彻底“摆烂”。

转眼到了16岁上高一的年纪，“感性”的许埈珥选择辍学写诗：

我听到好听的音乐时，真的会流眼泪。”

我知道自己很聪明，但无法用成绩来证明这一点，所以开始写诗。

当时，他写了一些关于自然和自己经历的东西，想在读大学之前的两年内完成全部作品。

不过他发现写作过程有些痛苦和压抑，也只是喜欢成为伟大诗人后身上的那种光环，再加上写诗养不活自己，

慎重考虑之后，还是回到学校读完高中并考了大学。

进入首尔国立大学时许埈珥19岁，这个年龄还不算晚，但他仍然觉得很迷茫：不知道自己想做什么，也不知道自己擅长什么。

△来源：quantamagazine

因为曾经想过当科学记者，他就选择了主修天文学和物理，但最终还是以经常逃课、多门课程重修收场。

我大概是迷路了。

24岁时，同班同学早就毕业了，他还没有，硬生生读到了第六年。

不过说来也巧，“幸好他还没毕业”，遇到了来学校访问并讲学的菲尔兹奖得主广中平佑(Hironaka)。

因为想把这个大名人作为自己的第一个采访对象，他参加了他开的代数几何课。

没想到的是，自己就被这位老师的魅力吸引住了，而且他发现课程本身也很有意思：不像普通本科课程那样“精巧”，反而很“简化”。

开窍了，数学封印解除！

他越来越觉得数学居然这么有意思，而且和写诗不同：

在数学里不会过度关注自我，可以自由寻找“在自己之外的美”，而这种美是一种客观的、真实的东西，比写作更能让自己敞开心扉。

与此同时，与相当诗人的那段时间不同，学数学也让他不再总是想要寻求外界的认可。

就这样，许埈珥成为了广中平佑班上最积极的学生——

当时200人的班上几个星期后就只剩5名同学，他坚持到了最后。

广中平佑看到了许埈珥的潜力，也把他收到了靡下。

就这样，许埈珥和这位老师一起吃饭、交流数学想法，尤其是从他身上学到了霍奇理论。

就连广中平佑回日本，许埈珥也都跟着。

ps.有意思的是，许埈珥最开始主动去找广中平佑吃午饭，主要是希望问一些他的个人信息作为采访素材，结果广中平佑总是把话题转移到数学上来。

不过许埈珥装作听得懂的样子，教授后来回忆这件事，表示还真不记得原来他根本没有听懂。

醉心数学，几个月以冷冻披萨为生、妻子分娩还在解题

其实，除了前面提到的“波折”的数学开窍经历，许埈珥身上还有一些有意思的小插曲。

许多和他共事的人对他的评价是：非常谦虚、脚踏实地。

得知自己获得菲尔兹奖时，他表示，确实很高兴，但内心深处会怀疑自己真的有这么优秀吗？

Quanta Magazin的记者在对他进行采访时，发现他说话其实很慢、用词谨慎、经常停顿，以一种非常平和、平静的方式来表达自己。

这和另一位合作者对他的评价一样：

许埈珥是一个不会很容易兴奋的人。如果你和他聊5分钟微积分，你会觉得这人可能连资格考试都过不了。

但事实上，他是在以一种更深入的方式理解一些看似简单的概念，这些东西后来都被证明很有用。

△来源：quantamagazine

在生活中，许埈珥自诩是一个非常能忍受重复性的人，每天都保持着同样的生活规律。

他办公室里的东西很少，经常在公共图书馆吵闹的儿童区工作，因为安静的地方会让他打瞌睡。

他痴迷于数学，不愿意浪费时间做饭，曾经几个月都靠冷冻比萨饼为生。

博士毕业后搬家赶上冬天，家里没有毯子。

他嫌购物中心太远浪费时间，就在附近的药店买了十块布+一个巨大的订书钉，给自己做了个毯子。

……

如此种种，以至于他在韩国读硕士时认识的女朋友来看他，发现他“生存技能如此堪忧”之时，都在犹豫要不要嫁给他。

△来源：quantamagazine

嫁过去之后，结果又在生孩子时，他还在做数学题……

好在孩子出生以后许埈珥“收敛”了很多，也能放下时间陪孩子玩耍、做家务。

不变的是，许埈珥仍然一天只能集中精力工作几个小时。

妻子形容他：“别人工作1小时，休息5分钟，他一小时都在干别的，然后专注5分钟、10分钟。”

今年还有一位女数学家得奖

许埈珥这位数学家的精彩故事讲完了，今天和他一起得奖的其他三位数学家同样值得关注。

第一位是来自牛津大学的教授James Maynard，他的研究方向是数论。

获奖理由：因对解析数论的贡献而被授予2022年菲尔兹奖，该贡献使得素数结构和迪奥芬图逼近的理解方面取得了重大进展。

相信有很多对他已经有所熟悉，他曾摘得「数论界最高奖」柯尔奖，证明孪生素数猜想的办法连另一位菲尔兹奖得主陶哲轩都自叹弗如。

第二位是来自瑞士日内瓦大学/法国高等科学研究所的教授Hugo Duminil-Copin，他的研究方向是概率论。

获奖理由：因解决了统计物理中相变概率理论的长期问题，特别是在三维和四维领域的问题。

最后一位是就职于瑞士洛桑联邦理工学院的乌克兰数学家Maryna Viazovska。

她是史上第二位获得此奖的女数学家（首位是37岁的伊朗数学家Maryam Mirzakhani，于2014年获得），研究方向和许埈珥一样，是组合几何。

获奖理由：因为她证明了在8维空间中E8晶格提供相同球体下的最密集封装，并进一步为傅里叶分析中的相关极值问题和插值问题做出贡献。

最后，迄今为止，一共有64位数学家获得菲尔兹奖，大部分获奖者为美国人和欧洲人，亚裔获得者少之又少：

至今共11位，熟知的除了我们的丘成桐教授（1982年获奖），还包括越南数学家吴宝珠（2010年）和华裔数学家陶哲轩（2006年）。

后面两位曾经在同一届IMO比赛中同时获得金牌。

参考链接：
[1]https://www.quantamagazine.org/june-huh-high-school-dropout-wins-the-fields-medal-20220705/
[2]https://www.quantamagazine.org/a-path-less-taken-to-the-peak-of-the-math-world-20170627/
[3]https://news.sciencenet.cn/htmlnews/2022/7/482148.shtm
[4]https://www.maigoo.com/news/539426.html

— 完 —

「量子位·视点」直播报名

什么是“智能决策”？智能决策的关键技术是什么？它又将如何打造引领企业二次增长的“智能抓手”？

7月7日周四，参与直播，为你解答～

点这里👇关注我，记得标星哦～