Leetcode 1240：铺瓷砖（超详细的解法！！！）

你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。

房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。

假设正方形瓷砖的规格不限，边长都是整数。

请你帮设计师计算一下，最少需要用到多少块方形瓷砖？

示例 1：

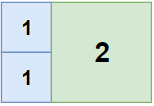
输入：n = 2, m = 3
输出：3
解释：3 块地砖就可以铺满卧室。2 块 1x1 地砖1 块 2x2 地砖

示例 2：

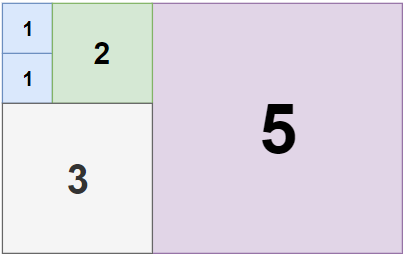
输入：n = 5, m = 8
输出：5

示例 3：

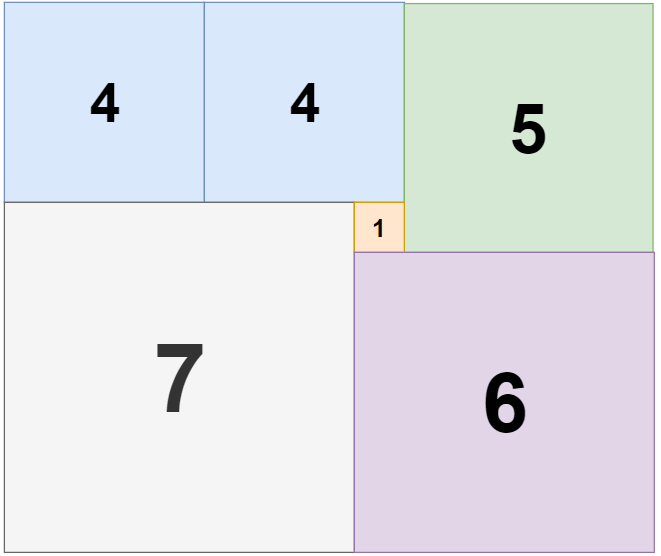
输入：n = 11, m = 13
输出：6

提示：

• 1 <= n <= 13
• 1 <= m <= 13

解题思路

这是一个经典的问题，该问题源自这篇论文Tiling a rectangle with the fewest squares。当然我们这里肯定不会这么复杂的去做，这里给出两种解法。

首先考虑dfs的解法，也就是一行一行的去枚举可以放的矩形，例如：

此时我们将第一行的所有矩形都确定了，接着考虑第二行的矩形，那么这里应该是从绿色（第2个）下面开始放，然后再放紫色的（第4个），也就是从最低高度开始放。当所有矩形的高度都是大矩形的高度n时，那么此时摆放成功，记录结果。为了记录每个矩形的高度，我们需要开辟m大小的数组（记录每个位置的高度）。对于第一个例子，最后记录（最后一层）的就是[1,2,2]。需要注意的是，我们实际放正方形的时候采用贪心策略（从最大的开始放），所以并不会出现上图中的情形。

最后代码非常简洁：

class Solution:def tilingRectangle(self, n: int, m: int) -> int:res = m * n    def dfs(ht, moves):if all(h == n for h in ht):res = min(res, moves)returnif moves >= res:returnidx = ht.index(min(ht))for i in range(min(m - idx, n - ht[idx]), 0, -1):# 正方形大小nht = ht[:]for j in range(i): # 正方形放入nht[idx + j] += idfs(nht, moves + 1) dfs([0] * m, 0)return res

这个问题还可以换一种方式思考，仔细观察题目给的例子，实际上描述了三种切分方式：横切、竖切和包含中心正方形的切分（第三个图）。

对于横切来说，最后的结果就应该来自上面一个矩形和下面一个矩形；对于竖切来说，最后的结果就应该来自左边一个矩形和右边一个矩形；对于包含正方形的形式来说，可以看成下面这种方式：

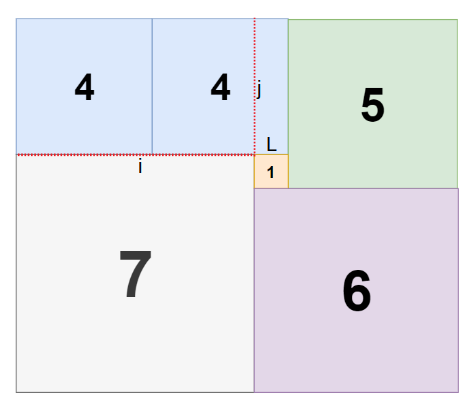
将左上角两个正方形何在一起看，我们需要确定中心矩形的大小l和位置(i,j)，那么左上角矩形的大小就是(i+l,j)，右上角矩形的大小就是(x-(i+l),j+l)，左下角矩形的大小就是(i,y-j)，右下角矩形的大小就是(x-i,y-(j+l))，其中x和y表示外部整个矩形的宽度和高度。

接着思考边界问题，当x==y的时候，只要一个正方形就可以了。而当x==1的时候，需要y个正方形。当y==1的时候，需要x个正方形。

from functools import lru_cache
class Solution:def tilingRectangle(self, n: int, m: int) -> int:@lru_cache(None)def dfs(x, y):if x == y:return 1if x == 1:return yif y == 1:return xres = x * yfor i in range(1, x//2 + 1):# 竖切res = min(res, dfs(i, y) + dfs(x - i, y))for j in range(1, y//2 + 1):# 横切res = min(res, dfs(x, j) + dfs(x, y - j))for l in range(1, min(x, y)):# 包含中心for i in range(1, x-l):for j in range(1, y-l):res = min(res, dfs(i+l, j) + dfs(x-(i+l), j+l) + dfs(i, y-j) + dfs(x-i, y-(j+l)) + 1)return resreturn dfs(n, m)

上面这个代码还可以继续优化，我们可以去掉包含中心的情况。因为题目给的数据最大是13，而包含中心矩形的最优解只会出现在(11,13)和(13,11)这两种情况的时候，此时的最优解是6，可以查看这个表。

from functools import lru_cache
class Solution:def tilingRectangle(self, n: int, m: int) -> int:@lru_cache(None)def dfs(x, y):if (x, y) in {(11, 13), (13, 11)}:return 6if x == y:return 1res = x * yfor i in range(1, x//2 + 1):res = min(res, dfs(i, y) + dfs(x - i, y))for j in range(1, y//2 + 1):res = min(res, dfs(x, j) + dfs(x, y - j))return resreturn dfs(n, m)

reference:

https://www.bilibili.com/video/av73704545?from=search&seid=6528127797779899524

我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！