PBR学习笔记（一）应用光学

本文主要是介绍PBR学习笔记（一）应用光学，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

为了系统的学习PBR，我准备先学习《应用光学》其中相关的几个章节。

地址：https://www.bilibili.com/video/av28799135?p=1

我看的教材是应用光学（第三版）张以谟。

第一章应用光学绪论

应用光学包括几何光学、典型光学系统和像差理论三大部分。我们先学习几何光学，它撇开光的波动本质，仅以光线作为基础利用几何分析方法来抽象研究光线经光学系统（包括平面、球面等）的传播和成像规律，利用足够精确的近似，简化复杂的光成像。

几何光学基本概念

发光点、波面、光线和光束

发光点——本身能发光或被照明后发光的几何点。即无大小又无体积，但能辐射能量。

波面——发光点在某一时刻发出的光形成波面。若周围是各向同性均匀介质，将形成以发光点为中心的球面波（无穷远处变为平面波）。

光线——波面的法线即几何光线中所指的光线。

光束——波面的法线簇，分为发散光束和汇聚光束。

几何光学的基本定律

光的直线传播定律

光在各向同性的均匀介质中沿直线传播。

衍射： $sin\alpha =K\lambda /D$ （K：衍射系数）

当波长 $\lambda \rightarrow 0$ 时（相对于衍射直径D，换句话说D足够大的时候），波动光学→几何光学。

光的独立传播定律

从不同的光源发出的光束以不同方向通过雪间某点时，彼此互不影响，各光束独立传播。

忽略干涉现象。

反射定律与折射定律：

PQ为一理想的光滑反射界面，入射光线AO和界面上投射点的法线ON夹角AON称为入射角，以I表示，反射光线OB和法线ON的夹角BON称为反射角，以I"表示。角I 和角I"以锐角来量度，由光线转向法线，顺时针方向旋转形成的角度为正，反之为负。

反射定律:入射光线、反射光线和投射点法线三者在同一平面内，入射角和反射角二者绝对值相等、符号相反，即入射光线和反射光线位于法线的两侧。反射定律可表示为:

$I=-{I}''$

PQ为两种均匀介质的理想平滑分界面，AO为入射光线，在O点发生折射，OC为相应的折射光线。NN"为入射点O的法线，入射角AON，以I表示；折射光线OC和法线NN"的夹角CON" 为折射角，以I“表示。入射角和折射角的符号法则也是从光线转向法线，按锐角来量度，顺时针方向旋转形成的角度为正，反之为负。

折射定律：入射光线、折射光线和投射点的法线三者在同一平面内，入射角的正弦与折射角的正弦之比与入射角的大小无关，而与两种介质的性质有关。对一定波长的光线，在一定温度和压力的条件下，该比值为一常数，等于折射光线所在介质的折射率n' 与入射光线所在介质的折射率n 之比。折射定律可以表示为：

$\frac{sinI}{sin{I}'}=\frac{{n}'}{n}$ 或 $nsinI = {n}'sin{I}'$

一定波长的单色光在真空中的传播速度c 与官在给定介质中的传播速度v之比，定义为该介质对指定波长的光的绝对折射率.：

n = C/v (C——光在真空中的速度，v——光在介质中的速度，n > 1)

在给定介质中，一定被茸的光的速度为常数，所以该被佳的绝对折射率也为常数。被分界面分开的两种介质，折射率高的光速低，称为光密介质:折射事低的光速高，称为光疏介质。

空气的绝对折射率受温度和压力的影响，标准条件下n = 1.000272（760mmHg，20℃，λ=0.5893μ），与空气比较的折射率叫做相对折射率（或者也可以说在空气中测得的介质折射率为工业折射率，简称折射率）。

光线传播的可逆性

一条光线由介质1 经分界面折射进入介质2 ，则折射定律可写为
$\frac{sinI_{1}}{sin{I_{2}}}=\frac{{n_{2}}}{n_{1}}$
另一条光线由介质2 经分界面折射进入介质1 ，如果光线的入射角为ι ，则按折射定律有
$\frac{sinI_{2}}{sin{I_{1}}}=\frac{{n_{1}}}{n_{2}}$
显然可以看出，以上两种折射情况是沿着同一光路，只是方向是相反的。这种现象称为"光路的可逆性"。

对于反射和折射现象，在均匀折射率介质和非均匀折射率介质、简单光学系统和复杂光学系统中，光的可逆性均是成立的。

在折射定律中若令n‘ = -n得I’ = -I，此时就是反射定律，也就是说反射定律是折射定律得特殊情况。其中-n并不代表负折射率，这是为了统一反射和折射得公式（空气中反射时，可以认为n=1，n’=-1）。

老师说也有负折射率，即入射光线和折射光线在法线同一侧，负折射率材料也是研究的一个热点。

分界面上反射光和折射光的能量分布

折射定律和反射定律只能解决反射光和折射光所遵循的方向的问题，而不能说明能量的分布。后者是物理光学中所要解决的问题。此处只给出结论。根据光的电磁理论，反射光和折射光的能量分布通常采用反射率R和透过率T表示:

R = 反射光的辐射通量 / 入射光的辐射通量

T = 折射光的辐射通量 / 入射光的辐射通量

在不存在吸收和其他损失的理想条件下，有

T = 1 - R

T和R的能量分布取决于入射光的偏振态、两种介质的折射率以及入射角的大小。当入射光为自然光，并给定界面两边的介质时，则反射光和折射光的能量分布主要取决于入射角的大小。

曲线A是光从空气进入玻璃(由光疏介质进入光密介质)时，分界面处的反射率凡和入射角I的关系曲线。曲线表明，当1<45°时，反射率 $R_{m}$ 近似于常量，近似于垂直入射(I = 0°) 时的反射率值 $R_{m0}$ ，按物理光学自然光垂直入射(I=0°)时的反射率:

$R_{m0} = \left (\frac{n - 1}{n + 1} \right )^{2}$

若n= 1.523 ，则 $R_{m0}\approx 0.043$ ，即约有4%的能量被反射。

曲线B是由玻璃进入空气(由光密介质进入光疏介质时)，分界酷的 $R_{n}-I$ 曲线。当l<41°时， $R_{n}\approx R_{n0}\approx 0.043$ ，反射率近似于一个常数.当I增大到41°时，反射率急剧上升到近似于1的值。当l>41°时， $R_{n}$ = 1 ，表明入射光线全部反射回原介质，没有折射发生，即所谓的"全反射"。

全反射

当光线的入射角I大于某值时，两种介质的分界面把入射光全部反射回原介质中去，这种现象称为"全反射"或"完全内反射"。

产生全反射的条件有:入射光由光密介质进入光疏介质:入射角必须大于一定的角度，按折射定律，当折射角 $I{}'$ = 90°，有

$sinI_{m}=\frac{{{n}'}}{n}sin90^{\circ}=\frac{{{n}'}}{n}$

式中，入射角 $I_{m}$ 称为临界角，此时折射光线沿分界面掠射。若入射角I 大于临界角 $I_{m}$ 时，折射定律已不适用。实验证明，此时光线不发生折射，而按反射定律把光线完全反射回原介质中。如果光线由玻璃射入空气，当玻璃的折射率n = 1. 523 时，则临界角 $I_{m}$ 约为41° ，与上一节一致。

在实际应用中，全反射常优于一般镜面反射，因为镜面的金属镀层对光有吸收作用，而全反射在理论上可使入射光全部反射回原介质。因此，全反射现象在光学仪器中有着重要的应用。例如，为了转折光路常用反射棱镜取代平面反射镜。

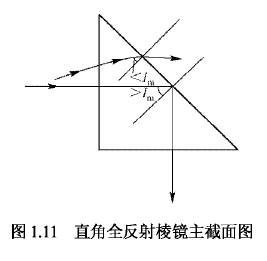
传光和传像的光学纤维也是利用了全反射原理。光纤将低折射率的玻璃外包层包在高折射率玻璃心子的外面:

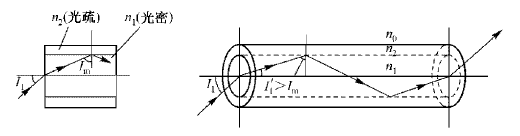
矢量形式的折射定律和反射定律

$A^{0}$ 和 ${A^{0}}'$ 分别表示入射光线和折射光线的单位矢量n和n'分别表示折射面两边的介质的折射率。矢量AO和AO'指向右方为正方向，反之为负方向。NO为折射面投射点法线的单位矢量，其方向顺着入射光线方向。由 $nsinI = {n}'sin{I}'$ 推出，折射定律可以表示为

$n(A^{0}\times N^{0} )=n{}'({A^{0}}'\times N^{0})$

把入射光线矢量A和折射光线矢量A'的长度各取为n和n'，即 $A = nA^{0}$ , $A{}' = n'{A^{0}}'$ ，则得

$A\times N^{0} = A{}'\times N^{0}$ 或 $(A-A{}')\times N^{0} =0$

此式说明矢量(A'-A) 和NO的方向是一致的，故可写为

$A-A{}'= GN^{0}$

G称为偏向常数。用 $N^{0}$ 对上式两边作点积，可得

$G = n{}'cosI{}' - ncosI$

由G的正负即比较n和n'的大小可得，矢量(A'-A) 和NO的方向由光疏介质进入光密介质时同向，光密介质进入光疏介质时反向。

由 $n{}'cosI{}' =\sqrt{{n}'^{2} - {n}'^{2}sin^{2}I{}'} =\sqrt{{n}'^{2} - n^{2}sin^{2}I} = \sqrt{n^{2} - n^{2}+ n^{2}cos^{2}I}$ 可得：

$G = \sqrt{{n}'^{2} - n^{2} + (N^{0}\times A)^{2})} - N^{0}\times A$

求得G值后，就可求得折射光线方向为：

$A{}'= A + GN^{0}$ （按照之前推是 $A{}'= A - GN^{0}$ ）

这就是矢量形式的折射定律。

和可逆性那小节一样，令n'=-n，得I=-I，则等式可写为：

$G = n{}'cosI{}' - ncosI = - 2ncosI =-2(N^{0}\times A)$

可得矢量形式的反射定律：

$A{}'= A -2N^{0}(N^{0}\times A)$

第六章光能及其传播计算

辐射能通量，光通量

辐射量

辐射能——以电磁辐射形式发射、传输或接受的能量称辐射能。单位为焦耳（J），尔格（erg）

辐射能通量/辐射功率——单位时间内通过某一面积的全部辐射能。符号为P，单位为瓦特（W）。

光是电磁辐射波谱中的一部分。发射辐射能的物体，称为一次辐射源。受别的辐射源照射后透射或反射能量的物体，称为二次辐射源。两种辐射源统称为辐射体，它可以是实物，也可以是实物所成的像。

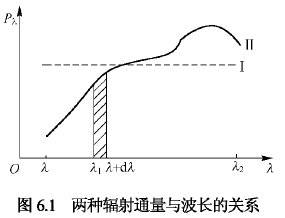
辐射可能由多种波长组成，每种波长的辐通量又可能各不相同。总的辐通量应该是各个组成波长的辐通量的总和。如下图所示Ⅰ，Ⅱ两种辐射，Ⅰ是等能量分布的辐射，Ⅱ是不等能量分布的辐射。设 $P_{\lambda }$ 是辐通量随波长变化的函数，在极窄的波段范围dλ内所对应的辐通量(图中阴影线所示面积)为

$dP = P_{\lambda }d\lambda$

总的辐通量为

$P = \int P_{\lambda }d\lambda$ (6.1)

接收器的光谱晌应

接收器对所能感受的波长是有选择性的。一种类型的接收器只能感受一定的波长范围，且对各种波长的响应程度(反应灵敏度)也不相同。

接收器对不同波长电磁辐射的反应程度称为光谱响应度或光谱灵敏度，对人眼来说有一个专门术语，称为光谱光视效率(spectral Luminous Efficiency) ，又译作"视见函数"。

由实验测得人眼对不同波长的光谱光视效率V(λ) 的数值列于下表6.1，对应的曲线如下图6.2所示。

下面λ写作l

实验表明，在同等辐射功率的情况下，频率为 $540\times 10^{12}$ Hz的单色辐射(空气中波长为0.555μm的黄绿光)对人眼造成的光剌激强度最大，光感最强，取其相对剌激强度为1 ，其余波长的V(l)均小于1 。例如波长为0.660μm的红光，V(I) = 0.06100，需要有比0.555μm的黄绿光大1/0.061 = 16 倍的功率才能对人眼造成同样的视觉剌激。或者说，黄绿光对人眼的剌激比同样功率的红光或蓝光要强。当人眼看到一束黄光比一束红光亮时，实际上红光的功率基本上比黄光的功率大。

光通量(Luminous Flux)

本章主要讨论可见光的能量，但涉及的原理、名词、定义等同样也适用于不可见光的辐射能量。为了区别，在有关可见光的名词前冠以"光"字，例如"光通量"和"辐通量"相对应，前者用于可见光，后者用于其他辐射能。

如前所述，式(6.1)的辐通量中只有0.38～0.77μm的辐射才能引起人眼的光刺激，且光剌激的强弱不仅取决于图6.1中辐射体辐通量的绝对值，还取决于人眼的光谱光视效率V(I)。定义辐射能中能被人眼感受的那一部分能量为光能。辐射能中由V(I)折算到能引起人眼刺激的那一部分辐通量称为光通量，用F表示(有的书上用F表示)。

在全部波段范围内，总光通量为

$\textbf{F} = \int P_{l}V(l)dl$

辐射通量和光通量同为功率，单位都是瓦特(W)，但是在有关可见光能的问题中，光通量F的通用单位为"流明"(lm)，关于流明的定义参见6.2节。

光通量和辐通量之间的换算

由理论和实验可知，1瓦特的频率为 $540\times 10^{12}$ Hz的单色辐射的辐通量等于683lm的光通量。对其他波长的单色光，lW辐通量引起的光刺激都小于683lm：

$\textbf{F} = 683\int P_{l}V(l)dl$

注意这个公式单位是lm，描述光通量，上面的公式单位是W，描述辐射通量。

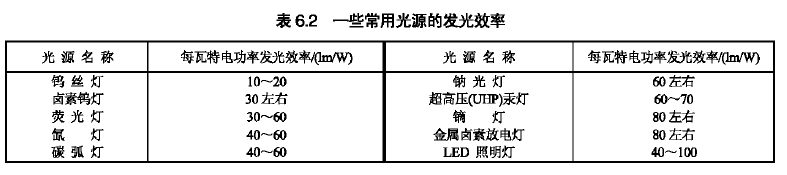
每瓦特电功率所产生的光通量(lm数)作为该类光源的发光效率：1W电功率的发光效率 = 该光源的光通量(lm)/该光源的耗电功率(W)

发光强度

立体角

以立体角顶点为球心，作一个半径为r的球面，用此立体角的边界在此球面上所截的面积dS除以半径的平方来标志立体角的大小，即

$d\omega =dS/r^{2}$

立体角的单位为"球面度" (Steradian)，符号为sr。当所截出的球面积等于半径的平方时，为一球面度。一个发光点周围全部空间的立体角为全部球面积/ $r^{2}$ ：

$\frac{4\pi r^{2}}{ r^{2}} = 4\pi(sr)$

立体角的计算

球面上一块小面积dS对点O构成的立体角为dω。面积则由边长a及b决定，由图可知： $a = rsini\mathrm{d}j$ ， $b = r\mathrm{d}i$ ， $dS = r^{2} sini\mathrm{d}i\mathrm{d}j$ ，小面积对应的立体角为

$\mathrm{d}\omega = \mathrm{d}S/r ^{2} = sin i\mathrm{d}i\mathrm{d}j$

这是立体角计算的普遍式。但在光学系统中习惯用平面角U来标志孔径角的大小，为此，下面建立平面角(孔径角)U和立体角ω之间的关系式，如图6.5所示。利用上式，立体角ω可写为

$\omega =\int\int sin i\mathrm{d}i\mathrm{d}j = \int_{0}^{2\pi}\mathrm{d}j\int_{0}^{U}sini\mathrm{d}i=4\pi sin^{2}(U/2)$ (6.6)

上式就是立体角和平面角的转换关系式。

当角U很小时， $sin(U/2)\approx U/2$ ，则

$\omega \approx \pi U^{2}$

我们也可以把立体角视作由无数个同心圆组成，用周长来积分计算，周长C=2πrsinθ， $\mathrm{d}s = 2\pi rsin\theta \cdot r \mathrm{d}\theta$ ，对其从0到U积分。

$s=\int_{0}^{U}2\pi r^{2}sin\theta \mathrm{d}\theta =-\int_{0}^{U}2\pi r^{2} \mathrm{d}cos\theta=2\pi r^{2}(1-cosU)=4\pi r^{2} sin^{2}(U/2)$

$w = s / r^{2} =4\pi sin^{2}(U/2)$

当角U很小时，可以近似看作是半径为rU的圆， $w\approx \pi \left ( rU \right )^{2}/r^{2} = \pi U^{2}$

发光强度

发光强度的符号为I。多数光源在不同方向辐射的光通量是不相等的，例如，常用的220V，100W钨丝白炽灯泡向各方向辐射的光通量如图6.7所示，曲线Ⅰ表示灯泡周围光通量分布情况。曲线Ⅱ表明该灯泡上部套上涂白的反光罩后光通量重新分布情况，可在某些方向上提高光能利用率。为了表征辐射体在空间某一方向上的发光状况，引入一个量"发光强度"。

发光强度的定义是某一方向单位立体角内所辐射的光通量值。设一点光源(实际上几何尺寸为零的点光源是不存在的，但当光源尺寸α较小，并从10a 以外的距离处观测时，可以近似地当做点光源处理，所引入的误差不大于1%)非均匀地向各方向辐射光能如图6.8所示。如果在某一方向上一个很小立体角dω内辐射的光通量为dF，则

$I=\mathrm{d}\mathbf{F}/\mathrm{d}\omega$ （6.8）

式中，I称为点光源在该方向上的发光强度。

如果点光源在一个较大的立体角ω范围内均匀辐射，其总光通量为F ，则在此立体角范围内的平均发光强度为常数，即：

$I=\mathbf{F}/\omega$

发光强度的单位

发光强度I的单位为坎德拉(Candela) ，符号为cd，它是光度学中最基本的单位。其他单位(如光通量、光照度、光亮度等的单位)都是由这一基本单位导出的。

坎德拉的定义为:一个频率为 $540\times 10^{12}$ Hz的单色辐射光源，若在给定方向上的辐射强度为1/683W/sr，则该光源在该方向的发光强度为1cd。定义中以频率取代波长，可以避免空气折射率的影响，使定义更严密:也可以使这一频率对应于空气中波长为0.555μm的单色辐射，即是对人眼光剌激最灵敏的波长。

发光强度的单位最早叫“烛光”（candle），在1881年，国际电工技术委员会根据科技发展和要求，把“烛光”规定为国际性单位，并定义为将一磅鲸鱼油脂制成六支蜡烛，以每小时120格令的速度燃烧时，在水平方向的发光强度为1烛光。而从烛光到坎德拉，无论是单位的定义还是复现计数，都经历了漫长的演变过程，大家可以查询相关的资料查看。

光通量的单位

由基本单位坎德拉可以导出光通量的单位流明(lumen) ，符号为lm。由式(6.8): dj = Idω，发光强度为1cd的点光源在单位立体角1sr内发出的光通量为定义1lm，即

$1lm =1cd\cdot sr$ （就是 $1cd=1lm / sr$ 转换）

光源发光强度和光通量之间的关系

各向均匀发光的点光源在立体角w内的总光通量为

$\mathbf{F} =I_{0}\omega$

$I_{0}$ 是平均发光强度。发向四周整个壁间的总光通量为

$\mathbf{F} = 4\pi I_{0}$

把平面孔径角U和立体角ω的换算关系式(6.6)代入

$\mathbf{F} = 4\pi I_{0}sin^{2}(U/2)$

也可以从这个表求得表6.2的发光效率。

光照度和光出射度

光照度定义及其单位

光照度(Illuminance)简称照度，用字符E表示。定义为：照射到物体表面一个面元上的光通量除以该面元的面积，即单位面积上所接收的光通量大小：

$E=\mathrm{d}\mathbf{F}/\mathrm{d}S$

dS为被照明面元的面积，dF为面元dS上所接收的光通量。如果较大面积的表面被均匀照明，则投射到其上的总光通量F除以总面积S称为该表面的平均光照度 $E_{0}$ ：

$E_{0}=\mathbf{F}/S$

光照度的单位为勒克斯，符号为lx，1lx是1lm的光通量均匀照射到1 $m^{2}$ 的面积上所产生的光照度。

点光源直接照射一平面时产生的光照度(距离平方反比律)

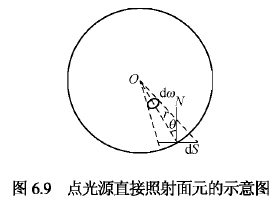
点光源O的平均发光强度为 $I_{0}$ ,面积dS距离O为r，对点O所张的立体角为dω ，dS的法线和dω的轴线夹角为q 。由立体角的定义可得：

$\mathbf{d}\omega =\mathbf{d}Scos \mathbf{q}/r^{2}$

光通量：

$\mathbf{d}\mathbf{F}=I\mathbf{d}\omega =I\mathbf{d}Scos \mathbf{q}/r^{2}$

面积dS上的光照度为：

$E=\mathbf{d}\mathbf{F}/\mathbf{d}S=Icos \mathbf{q}/r^{2}$

即点光源直接照射一面元时，其上的光照度与点光源的发光强度成正比，与点光源到面元的距离r的平方成反比，并与面元的法线和照射光束方向的夹角q的余弦成正比。

光出射度(Luminous Exitance)

光出射度用符号M表示。其定义为离开表面一点处的面元的光通量除以面元的面积，即从一发光表面的单位面积上发出的光通量称为该表面的光出射度。光出射度和照度E是一对相对意义的物理量，两者的单位相同(lm/ $m^{2}$ )。

对于非均匀辐射的发光表面，有：

$M=\mathbf{d}\mathbf{F}/\mathbf{d}S$

在较大面积上均匀辐射的发光表面，其平均光出射度为

$M_{0}=\mathbf{F}/S$

发光表面可以是本身发光的，也可以是受外来光照射后透射或反射发光的:可以是实际发光体，也可以是其像面。

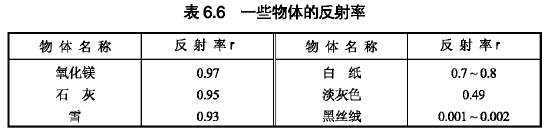
若一本身不发光的反射表面S受外来照射后所得的照度为E，入射光中一部分被吸收，另一部分被反射，设表面的反射率为r,r是反射光通量F'和入射光通量F之比，即r =F'/F，一般以百分数表示，则表面反射时的光出射度为：

${\mathbf{F}}'/S=r\mathbf{F}/S$

$M=rE$

所有物体的反射率都小于1。多数物体对光的反射有选择性，对不同波长的色光，有不同的反射率r。受白光照射时，若表面对红光的反射能力较强，而蓝、绿、黄等色光被吸收，则这种物体被人眼观察时表现为红色。对所有波长的反射率r值都相同且近似于零的物体称为黑体，严格而言，黑体是不管波长、入射方向或偏振状态如何，吸收所有辐射能的热辐射体。同时，在给定温度下，它对所有波长都具有最大的光谱辐射出射度，因此黑体又称为全辐射体。

光亮度

上节中的光出射度M虽能表征发光表面单位面积上发出的光通量值，但并未计入辐射的方向，不能全面地表征发光表面在不同方向上的辐射特性，为此须引入另一物理量一一光亮度(Luminance)，用字符L表示。

在评价视频画面质量时，还有一个名词Brightness(亮度，或译为明度、明亮度)。"Brightness"是考虑了观测环境、人眼性能，及光源本身一些影响因素后，人眼主观上感觉到的明亮程度。

光亮度的定义

光亮度简称亮度，用字符L表示。光亮度定义为在发光表面上取一块微面积dS，此微面积在与表面法线N夹i角方向的立体角dω内发出的光通量为 $\mathrm{d}\Phi_{i}$ ，则由前可知，i方向的发光强度为

$I_{i}=\mathrm{d}\mathbf{F_{i}}/d\omega$

微面积dS在i方向的光亮度 $L_{i}$ 的定义是微面积在i方向的发光强度I与此微面积在垂直于该方向的平面上的投影面积dScosi之比，即

$L_{i}=\frac{I_{i}}{\mathrm{d}Scosi}$ (6.21)

带入 $I_{i}$ ：

$L_{i}=\frac{\mathrm{d}\mathbf{F_{i}}}{cosi\mathrm{d}S\mathrm{d}\omega }$ (6.22)

i方向的光亮度 $L_{i}$ 是投影到i方向的单位面积上的发光强度，也就是投影到i方向的单位面积、单位立体角内的光通量大小。

光亮度的单位是坎德拉每平方米(cd/ $m^{2}$ )。

余弦辐射体

一般发光面在各个方向的亮度值不等，即亮度 $L_{i}$ 本身是空间方位角i和j的复杂函数。但某些发光面的发光强度与空间方向的关系按下列简单规律变化：

$I_{i}=I_{N}cosi$ (6.23)

$I_{N}$ 是dS法线方向的发光强度， $I_{i}$ 是与法线成i角方向的发光强度。符合上式规律的发光体称为"余弦辐射体"或"朗伯(Lambert)辐射体"。

把式(6.23)代入式(6.21) ，求出余弦辐射体的光亮度为常数 $L_{0}$ :

$L_{i}=I_{N}/dS=L_{0}$

一般的漫射表面都具有近似于余弦辐射的特性。在完全镜面反射(定向反射)中，反射光方向的亮度 $L_{i}$ 最大，其余方向为零，不具有余弦辐射性质。绝对黑体是理想的余弦辐射体。有些光源很接近于余弦辐射体，例如图6.16 中平面状钨灯的发光强度曲线接近于双向的余弦发光体。发光二极管(LED)辐射的空间分布近似于单向的余弦辐射体。

余弦辐射表面向孔径角为U 的立体角内发出的光通量

如图6.17所示，设dS为一个余弦辐射微表面，其通过垂直方向孔径角为U的立体角ω所发射的光通量，从(6.22)得：

$\mathrm{d}\mathbf{F_{i}}=L_{i} cosi\mathrm{d}S\mathrm{d}\omega$

$\mathbf{F}=\int L_{i} cosi\mathrm{d}S\mathrm{d}\omega$

余弦发光体的 $L_{i}$ 为常数,对U范围内的圆锥角积分，得

$\mathbf{F}=L\mathrm{d}S\int_{ 0}^{2\pi}\mathrm{d}j\int_{0}^{U}cosisini\mathrm{d}i=\pi L\mathrm{d}Ssin^{2}U$ (6.25)

余弦辐射面在孔径角U范围内发射的光通量正比于光亮度L、面积dS和孔径角正弦的平方。

点光源在孔径角U范围内发射的光通量正比于发光强度I；而余弦辐射的面光源在孔径角U范围内的光通量正比于光亮度L。光亮度在面光源中所起的作用与发光强度在点光源中的作用相似，是决定进入光学系统的光通量的重要指标。

余弦幅射表面向2π立体角空间发出的总光通量、光亮度和光出射度的关系

U=π/2时，由式6.25可得

$\mathbf{F}=\pi L\mathrm{d}S$

这是余弦发光面向2π立体角半球空间发出的全部光通量。再由光出射度的定义式得该余弦辐射体的光出射度为：

$M=\mathbf{F}/{d}S=\pi L$

小结：

光通量(Luminous Flux) 符号：F(Φ) 单位：lm(cd•sr)(W)

立体角(Solid Angle) 符号：ω(Ω) 单位：sr

发光强度(Luminous Intensity) 符号：I 单位：cd(lm/sr)

光照度(Illuminance) 符号：E 单位：lx(lm/ $m^{2}$ )

光出射度(Luminous Exitance) 符号：M 单位：lx(lm/ $m^{2}$ )

光亮度(Luminance) 符号：L 单位：cd/ $m^{2}$ (lm/ $m^{2}$ /sr)

$\textbf{F} = 683\int P_{l}V(l)dl$

$\mathrm{d}\omega = \mathrm{d}S/r ^{2} = sin i\mathrm{d}i\mathrm{d}j$

$I_{0}=\mathbf{F}/w$

$\omega =4\pi sin^{2}(U/2)$

$E_{0}=\mathbf{F}/S$

$E=\mathbf{d}\mathbf{F}/\mathbf{d}S=Icos \mathbf{q}/r^{2}$

$M_{0}=\mathbf{F}/S$

$L_{i}=\frac{I_{i}}{\mathrm{d}Scosi}=\frac{\mathrm{d}\mathbf{F_{i}}}{cosi\mathrm{d}S\mathrm{d}\omega }$

$\mathbf{F}=L\mathrm{d}S\int_{ 0}^{2\pi}\mathrm{d}j\int_{0}^{U}cosisini\mathrm{d}i=\pi L\mathrm{d}Ssin^{2}U$

光通量和光亮度在光学系统中的传递、像面光照度

同一介质内的元光管中光通量和光亮度的传递

元光管即两端的截面积很小的光管，光能就在此光管内传递。先讨论在同一介质中传递的情况。

图6.1 9 中由任意两个光束截面周界所围的锥体就是一个光管，图中虚线所示为光管周界。当两个截面尺寸很小(即小视场、小孔径的近轴区范围内)时就是元光管。

根据式6.22得由dS1面出发并经元光管传到dS2面上的光通量：

$\mathrm{d}\mathbf{F_{1}}=L_{1}cosi_{1}\mathrm{d}S_{1}\mathrm{d}\omega _{1}=\frac{L_{1}cosi_{1}\mathrm{d}S_{1}\mathrm{d}S_{2}cosi_{2}}{r^{2}}$

由于光线可逆，同样可以得到由dS2面发出并传到dS1面上的光通量：

$\mathrm{d}\mathbf{F_{2}}=L_{2}cosi_{2}\mathrm{d}S_{2}\mathrm{d}\omega _{2}=\frac{L_{2}cosi_{2}\mathrm{d}S_{2}\mathrm{d}S_{1}cosi_{1}}{r^{2}}$

如果光能在元光管中没有损失，则dF1= dF2。于是得 $L_{1}=L_{2}$ ，即光能在同一均匀介质的元光管中传递时，如果无光能损失，则在传播方向上任一截面上光通量的传递不变，光亮度的传递也不变，任一截面上光亮度相等。

面光源直接照射一平面时产生的光照度(距离平方反比律)

发光面dS1在被照明面dS2上造成的光照度E2：

$E_{2}=\frac{\mathrm{d}\mathbf{F_{1}}}{\mathrm{d}S_{2}}=\frac{L_{1}\mathrm{d}S_{1}cosi_{1}cosi_{2}}{r^{2}}$

面光源直接照射一微面积时，微面积的光照度与面光源的光亮度L和光源面积大小成正比，与距离r平方成反比，并与两平面的法线和光束方向的夹角i1，i2的余弦成正比。与点光源比较，点光源造成的光照度与发光强度成正比，而面光源造成的光照度和光亮度与光源面积成正比:两者的共同点是都与距离平方成反比，且都与表面的倾斜度有关，故称此关系为"距离平方反比律"。

（待续，请看教材，先贴上比较重要得一部分）

小视场、大孔径光学系统的光通量和像面照度

根据式6.25，如果从物面到像面传递过程中光能有损失，得

$\mathbf{{F}'}=K\mathbf{F}=K\pi L\mathrm{d}Ssin^{2}U$

像面中心部分的光照度E'为

${E}'=\frac{\mathbf{{F}'}}{\mathrm{d}{S}'}=K\mathbf{F}=K \pi L \frac{\mathrm{d}S}{\mathrm{d}{S}'}sin^{2}U=K \pi L \frac{y^{2}}{{y}'^{2}}sin^{2}U=K \pi Lsin^{2}U/b^{2}$