games101作业02：Triangles and Z-buffering

games101作业02：Triangles and Z-buffering

内容

1. 创建三角形的 2 维 bounding box。
2. 遍历此 bounding box 内的所有像素（使用其整数索引）。然后，使用像素中心的屏幕空间坐标来检查中心点是否在三角形内。
3. 如果在内部，则将其位置处的插值深度值 (interpolated depth value) 与深度缓冲区 (depth buffer) 中的相应值进行比较。
4. 如果当前点更靠近相机，请设置像素颜色并更新深度缓冲区 (depth buffer)。

基础知识

判断点是否在三角形内

叉乘在图形学中的意义：判断左和右
判断b在a的左边还是右边(右手坐标系)
用a叉乘b，得到的结果是正的，说明b在a的左侧
用b叉乘a，得到的结果是负的，说明b在a的右侧

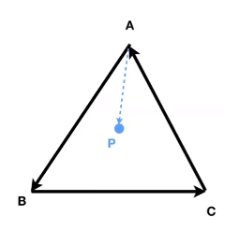
判断内和外
判断Q在三角形ABC的内部？
ABXAP，结果是正的，说明P在AB的左侧
BCXBP，结果是正的，说明P在AB的左侧
CAXPC，结果是正的，说明P在CA的左侧
所以P在三角形ABC的内部，
绕的顺序是AB-BC-CA，绕向逆时针和顺时针，也就是三个叉乘结果都是正的，或者都是负的，这个是三角形光栅化的基础，要知道三角形覆盖了哪些像素，判断像素是否在三角形内部

锯齿 (走样，Aliasing)

利用三角形光栅化算法，我们可以把该三角形表示成一个如下图所示的像素点集合

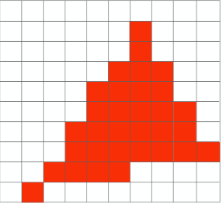
三角形变的“歪歪扭扭”的，哪能说它是一个标准的三角形呢。这种问题本质是因为我们在采样的时候的频率过低无法跟上图像的频率，导致最后结果的失真，当然这是从信号处理的角度去看这个问题，在这里不会做过多的展开。
从简单的角度去解释这种问题出现的原因就是，我们用有限离散的像素点去逼近连续的三角形，那么自然会出现这种锯齿走样的现象，因为这种近似是不准确的。接下来会介绍两种解决走样的方法，具体来说第二种可以当成第一种的改良

超采样反走样(Super Sampling AA)

SSAA的想法其实是非常直观的，如果有限离散像素点逼近结果不好，那么我们用更多的采样点去逼近不就会得到更好的结果了吗？所以根据这个思想我们可以把原来的每个像素点进行细分，比如下例中，我们讲每个像素点细分成了4个采样点：

我们根据每个采样点来进行shading（该概念还未提及，可以理解为计算每个像素点的颜色的过程，当然这里是一个纯红色的三角形，如果该点在三角形内，它的颜色值可以直接得到为（1，0，0）），这样得到了每个采样点的颜色之后，我们讲每个像素点内部所细分的采样点的颜色值全部加起来再求均值，作为该像素点的抗走样之后的颜色值！结果如下：

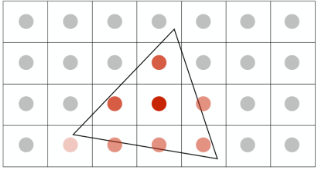
当然读者可能还是觉得，这还不是有锯齿，咋就抗锯齿了呢？

仔细观察可以发现因为将4个采样点的颜色求均值的之后，靠近三角形边缘的像素点有的变淡了，从宏观角度来看的话，这个锯齿就会变得不那么明显了。我们可以看看这样一个具体例子。

怎么样，效果还是相当明显吧！

(tips：SSAA并不局限于分成4个，也可以分更多的，可以自己决定，如果喜欢玩游戏的读者一定知道游戏里面其实就有一个抗锯齿的选项，其中的 ×2,×3,×4\times2,\times3,\times4×2,×3,×4,分别代表的就是4个，9个，16个采样点，显然采样点越多抗锯齿效果越好，但计算负担也会随之增加）。

1.2 多采样反走样(Multi-Sampling AA)
MSAA其实是对SSAA的一个改进，显然SSAA的计算量是非常大的，每个像素点分成4个采样点，我们就要进行4次的shading来计算颜色，额外多了4倍的计算量，如何降低它呢？

MSAA的做法也很容易理解，我们依然同样会分采样点，但是只会去计算究竟有几个采样点会被三角形cover，计算颜色的时候只会利用像素中心坐标计算一次颜色(即所有的信息都会被插值到像素中心然后取计算颜色)，如下图：

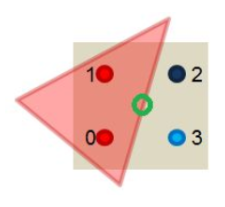
只有两个采样点被我们的三角形cover了，将该像素中心计算出来的颜色值乘以50%即可，这样大大减少了计算量，并且得到反走样效果也是很不错的。

Z-Buffer算法

解决了走样问题之后，还有一个仍需解决的问题，我们如何判断物体先后关系？更具体的说每个像素点所对应的可能不止一个三角形面上的点，我们该选择哪个三角形面上的点来显示呢？答案显然易见，离摄像头最近的像素点显示。这里便要利用到我们之前做model−>view−>projection变换之后所得到的深度值 zzz 了，这里定义z越大离摄像机越远！
以下我们介绍Z-Buffer算法，主要有2步。

1. Z-Buffer算法需要为每个像素点维持一个深度数组记为zbuffer，其每个位置初始值置为无穷大（即离摄像机无穷远）。
2. 随后我们遍历每个三角形面上的每一个像素点[x,y]，如果该像素点的深度值z，小于zbuffer[x,y]中的值，则更新zbuffer[x,y]值为该点深度值z，并同时更新该像素点[x,y]的颜色为该三角形面上的该点的颜色。

重心坐标求解

参考材料

给定三角形的三点坐标A, B, C，该平面内一点(x,y)可以写成这三点坐标的线性组合形式，即 (x,y)=αA+βB+γC且满足 α+β+γ=1。则称此时3个坐标A,B,C的权重α,β,γ为点(x,y)在重心坐标系下的重心坐标。
如何求解α,β,γ：

重心坐标插值（透视矫正插值）

在屏幕空间进行线性插值得到点c的intensity为0.5，然而对于在在view space之中正确的插值结果，可以很明显看到C的intensity绝不为0.5。这也就造成了插值的误差，应该去矫正！

首先先分别定义屏幕空间的比例为s，view space中为t，其余符号含义如下图所示：

为了简便证明，将点的坐标用2维表示，第一维为图中所示的x轴，第二维为z轴。
简而言之，我们的目标就是得出t与s的关系式，这样就可以正确的利用屏幕空间的系数s插值到正确的view space的结果，推导过程如下。
由上图所示的投影所造成的三角形相似性可以轻易得出如下几个式子：

同样，分别利用screen space 以及 view space的线性插值可以得到以下几个式子：

将4式与5式代入3式得：

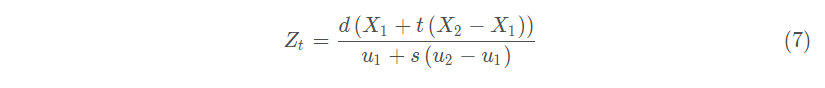
再将1式与2式代入7式得：

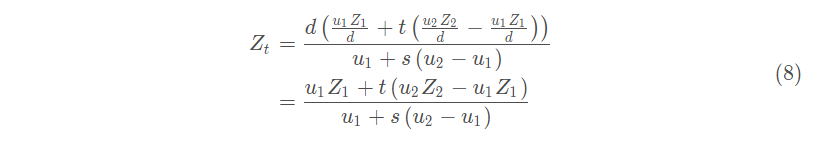
最后将6式代入8式的左边得到：

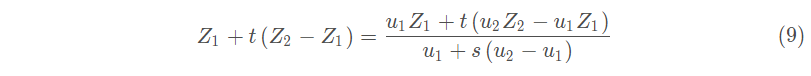
仔细观察9式，我们已经成功得出了t与s的一个关系式，其中的其它参数都是已知，因此进一步化简不在这里展开，可以得到如下t与s关系：

如此就可以利用屏幕空间下的系数得到正确插值结果了，计算如下：

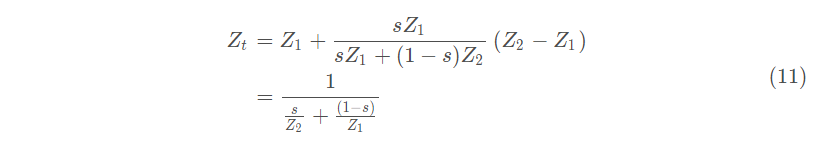
以上证明虽然只是针对线性插值的矫正结果，对于重心坐标插值，我们可以类似类推得出：

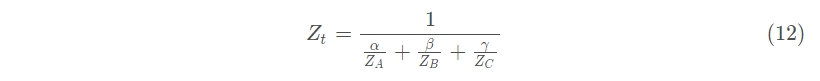
正确得出深度的插值结果之后，再看看任意属性(法线向量，纹理坐标，view space 坐标)插值结果，依然以线性插值为例先进行推导：用I代表任意属性

不难看出插值的分母就是深度值的倒数，类推得出重心坐标任意属性的正确插值如下:

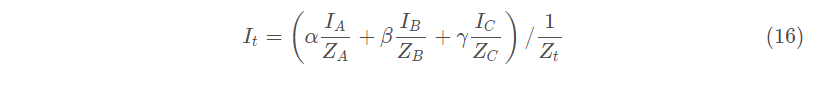
（tips:任意属性自然包括深度值，将深度值z代入16式可以得出与12式一样的结果）
至此，我们就可以利用16式进行所有的属性的重心坐标插值，并且保证结果正确了！

代码

static bool insideTriangle(int x, int y, const Vector4f* _v){Vector3f v[3];for(int i=0;i<3;i++)v[i] = {_v[i].x(),_v[i].y(), 1.0};Vector3f f0,f1,f2;f0 = v[1].cross(v[0]);f1 = v[2].cross(v[1]);f2 = v[0].cross(v[2]);Vector3f p(x,y,1.);if((p.dot(f0)*f0.dot(v[2])>0) && (p.dot(f1)*f1.dot(v[0])>0) && (p.dot(f2)*f2.dot(v[1])>0))return true;return false;
}

void rst::rasterizer::rasterize_triangle(const Triangle& t) {auto v = t.toVector4();// 构造bounding boxfloat min_x = std::min(v[0][0], std::min(v[1][0], v[2][0]));float max_x = std::max(v[0][0], std::max(v[1][0], v[2][0]));float min_y = std::min(v[0][1], std::min(v[1][1], v[2][1]));float max_y = std::max(v[0][1], std::max(v[1][1], v[2][1]));min_x = (int)std::floor(min_x);max_x = (int)std::ceil(max_x);min_y = (int)std::floor(min_y);max_y = (int)std::ceil(max_y);bool MSAA = true;//MSAA 4Xif (MSAA) {// 格子里的细分四个小点坐标std::vector<Eigen::Vector2f> pos{{0.25,0.25},{0.75,0.25},{0.25,0.75},{0.75,0.75},};for (int x = min_x; x <= max_x; x++) {for (int y = min_y; y <= max_y; y++) {// 记录最小深度float minDepth = FLT_MAX;// 四个小点中落入三角形中的点的个数int count = 0;// 对四个小点坐标进行判断 for (int i = 0; i < 4; i++) {// 小点是否在三角形内if (insideTriangle((float)x + pos[i][0], (float)y + pos[i][1], t.v)) {// 如果在，对深度z进行插值auto tup = computeBarycentric2D((float)x + pos[i][0], (float)y + pos[i][1], t.v);float alpha,  beta, gamma;std::tie(alpha, beta, gamma) = tup;float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();z_interpolated *= w_reciprocal;minDepth = std::min(minDepth, z_interpolated);count++;}}if (count != 0) {if (depth_buf[get_index(x, y)] > minDepth) {Vector3f color = t.getColor() * count / 4.0;Vector3f point(3);point << (float)x, (float)y, minDepth;// 替换深度depth_buf[get_index(x, y)] = minDepth;// 修改颜色set_pixel(point, color);}}}}}else {for (int x = min_x; x <= max_x; x++) {for (int y = min_y; y <= max_y; y++) {//下个采样点是否在三角形内if (insideTriangle((float)x + 0.5, (float)y + 0.5, t.v)) {auto tup = computeBarycentric2D((float)x + 0.5, (float)y + 0.5, t.v);float alpha;float beta;float gamma;std::tie(alpha, beta, gamma) = tup;float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();z_interpolated *= w_reciprocal;if (depth_buf[get_index(x, y)] > z_interpolated) {Vector3f color = t.getColor();Vector3f point(3);point << (float)x, (float)y, z_interpolated;depth_buf[get_index(x, y)] = z_interpolated;set_pixel(point, color);}}}}}
}