「LOJ#10056」「一本通 2.3 练习 5」The XOR-longest Path （Trie

本文主要是介绍「LOJ#10056」「一本通 2.3 练习 5」The XOR-longest Path （Trie，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题来自：POJ 3764

给定一棵

第一行一个整数

输出一行一个整数，表示答案。

样例输入

样例输出

样例解释

最长的异或和路径是 $1→2→31\to 2\to 31→2→3 ，它的长度是 3⨁4=73 \bigoplus 4=73⨁4=7。$

注意：结点下标从

注： $\bigoplus yx⨁y 表示 xxx 与 yyy 按位异或。$

对于 $100%100\%100% 的数据，1≤n≤105,1≤u,v≤n,0≤w<2311\le n\le 10^5,1\le u, v \le n,0 \le w < 2^{31}1≤n≤105,1≤u,v≤n,0≤w<231$

题解

首先对于树上两点路径的异或值，可以用一个树上前缀和维护。

记$sum[x]$为$x$到祖先的异或和。

由于异或有：$a ⨁ a = 0$

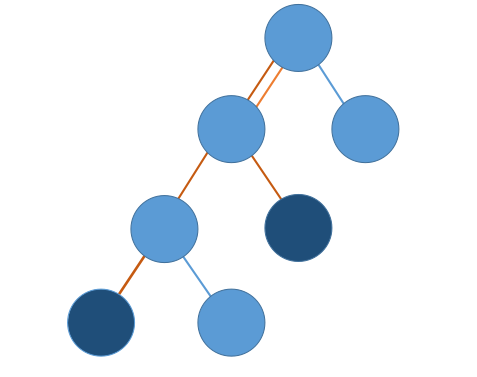
所以如下图，在$sum[u] ⨁ sum[v]$时，lca以上的屎色线已经被消掉了。

所以$ans=sum[u] ⨁ sum[v]$

问题转化为：有1e5个数，要求其中两数异或的最大值。

于是变为「LOJ#10050」「一本通 2.3 例 2」The XOR Largest Pair （Trie

于是这道题就可以由两道看起来离得很远的题拼起来而成了。

  1 编号     题目     状态     分数     总时间     内存     代码 / 答案文件     提交者     提交时间
  2 #231397     #10056. 「一本通 2.3 练习 5」The XOR-longest Path    Accepted     100     225 ms     10364 KiB     C++ / 1.8 K     qwerta     2018-10-16 16:53:15
  3 
  4 #include<iostream>
  5 #include<cstring>
  6 #include<cstdio>
  7 #include<cmath>
  8 using namespace std;
  9 inline int read()
 10 {
 11     char ch=getchar();
 12     int x=0;
 13     while(!isdigit(ch))ch=getchar();
 14     while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
 15     return x;
 16 }
 17 const int MAXN=1e5+3;
 18 struct emm{
 19     int e,f,v;
 20 }a[2*MAXN];//用来建树
 21 int h[MAXN];
 22 int tot=0;
 23 void con(int x,int y,int l)//连树边
 24 {
 25     a[++tot].f=h[x];
 26     h[x]=tot;
 27     a[tot].e=y;
 28     a[tot].v=l;
 29     a[++tot].f=h[y];
 30     h[y]=tot;
 31     a[tot].e=x;
 32     a[tot].v=l;
 33     return;
 34 }
 35 int d[MAXN],w[MAXN];//记深度和前缀和
 36 void dfs(int x)//dfs遍历树
 37 {
 38     for(int i=h[x];i;i=a[i].f)
 39     if(!d[a[i].e])
 40     {
 41         w[a[i].e]=(w[x] xor a[i].v);
 42         d[a[i].e]=d[x]+1;
 43         dfs(a[i].e);
 44     }
 45     return;
 46 }
 47 struct ahh{
 48     int nxt[2];
 49 }tr[3200003];//Trie树
 50 int cnt=0;
 51 int b[33];//用来按位拆分
 52 void add(int x)
 53 {
 54     int j=-1;
 55     memset(b,0,sizeof(b));
 56     while(x)//拆二进制
 57     {
 58         b[++j]=x&1;
 59         x>>=1;
 60     }
 61     int k=0;
 62     for(int j=31;j>=0;--j)
 63     {
 64         if(!tr[k].nxt[b[j]])
 65           tr[k].nxt[b[j]]=++cnt;
 66         k=tr[k].nxt[b[j]];
 67     }
 68     return;
 69 }
 70 long long find(int x)//返回与x异或的最大结果
 71 {
 72     int j=-1;
 73     memset(b,0,sizeof(b));
 74     while(x)
 75     {
 76         b[++j]=x&1;
 77         x>>=1;
 78     }
 79     long long now=0;
 80     int k=0;
 81     for(int j=31;j>=0;--j)
 82     {
 83         if(tr[k].nxt[1-b[j]])//尽量往不一样的走
 84         {
 85             now+=(1<<j);
 86             k=tr[k].nxt[1-b[j]];
 87         }
 88         else k=tr[k].nxt[b[j]];
 89     }
 90     return now;
 91 }
 92 int main()
 93 {
 94     //freopen("a.in","r",stdin);
 95     int n=read();
 96     for(int i=1;i<n;++i)
 97     {
 98         int u=read(),v=read(),w=read();
 99         con(u,v,w);//连树边
100     }
101     int s=min(7,n);
102     d[s]=1;
103     dfs(s);
104     long long ans=0;
105     for(int i=1;i<=n;++i)
106       add(w[i]);//加前缀和
107     for(int i=1;i<=n;++i)
108       ans=max(ans,find(w[i]));//记录答案
109     cout<<ans;
110     return 0;
111 }