这题看上去第一反应:
什么?平面几何???说好的A题呢???
读完样例&打完草稿:
这不就是个
xx题吗
回到正文,这题需要我们处理三种图形的嵌套:
- 圆形
- 等腰三角形(底边等于高)
- 正方形
这些嵌套其实总共只有六种情况,我们分类讨论(因为文中提到不会有一样的图形嵌套):
圆形
(1).圆形套三角形
如图,这种情况的三角形三个顶点和圆相交,对答案的贡献为3
(2).圆形套正方形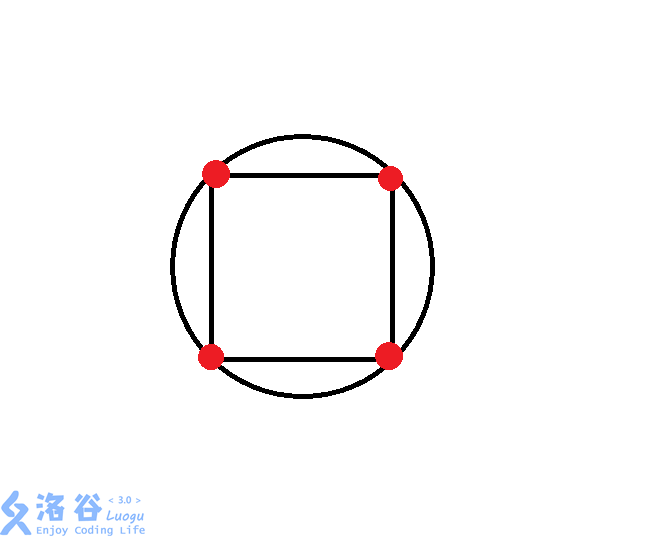
如图,这种情况的正方形四个顶点和圆相交,对答案的贡献为4- 三角形
(1).三角形套正方形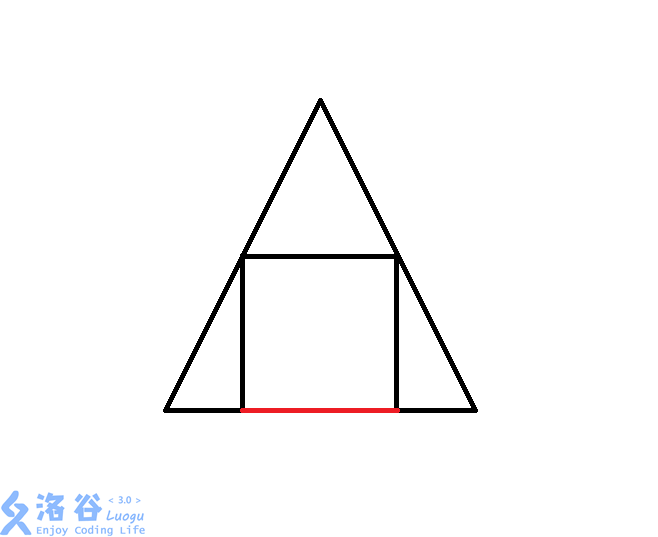
如图,这种情况的正方形会与三角形底边重合,所以有无限多个点
(2).三角形套圆形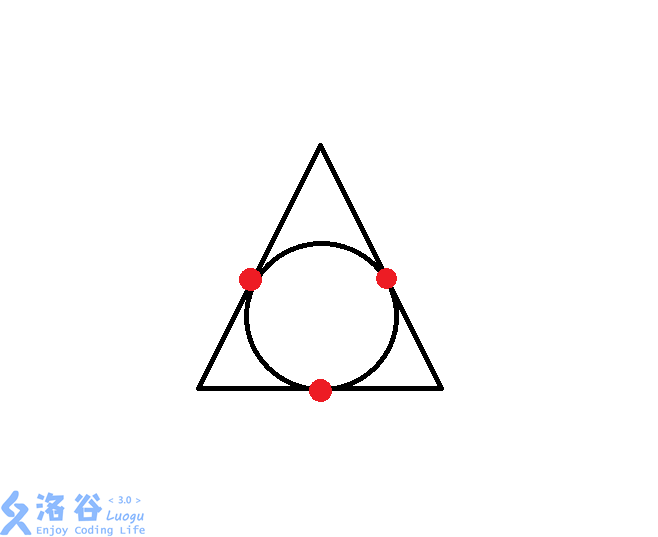
如图,这种情况的圆形会与三角形的三边相交,对答案的贡献(点数)为3 正方形
(1).正方形套圆形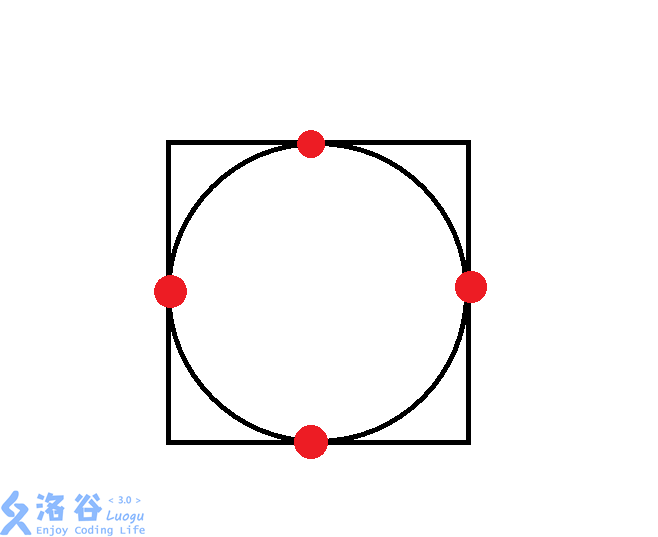
如图,这种情况的圆与正方形四边相交,对答案的贡献为4
(2).正方形套三角形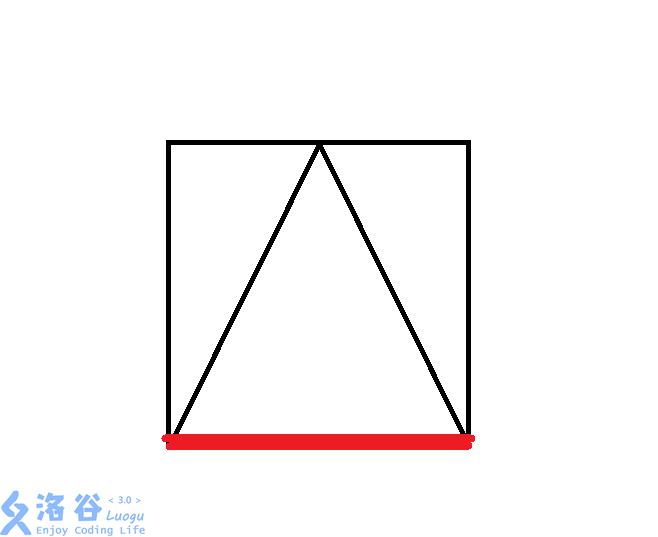
如图,这种情况的正方形会与三角形底边重合,所以有无限多个点
这样我们就可以写出一份看似正常的代码了:
#include <cstdio>
#include <cctype>
#define MAXN 101inline int read() {int a = 0,f = 1;char v= getchar();while (!isdigit(v)) {if (v == '-') {f = -1;}v = getchar();}while (isdigit(v)) {a = a * 10 + v- 48;v = getchar();}return a * f;
}int pre[MAXN],ans;int main() {int n = read();for (int i = 1;i <= n;++i) {pre[i] = read();}for (int i = 2;i <= n;++i) {if (pre[i-1] == 1) {if (pre[i] == 2) {ans += 3;}else {ans += 4;}}if (pre[i-1] == 2) {if (pre[i] == 1) {ans += 3;}else {printf("Infinite");return 0;}}if (pre[i-1] == 3) {if (pre[i] == 1) {ans += 4;}else {printf("Infinite");return 0;}}}printf("Finite\n%d",ans);return 0;
}笔者考试时,开开心心的拿着这份代码去交了,结果是:
WA!
为什么?
这里有一组数据可以hack掉这份代码:
Input:
3
3 1 2
Output:
Finite
6
程序输出:
Finite
7为什么?
我们可以画个图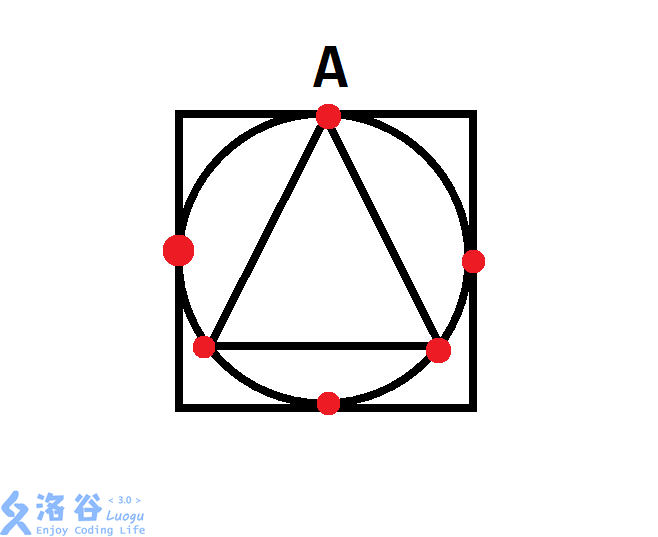
很明显,在计算圆形跟正方形,三角形与圆形的时候,A点被计算了两遍,这就是问题所在!
所以,我们要对所有形如这类的数据进行特判
加上特判的代码:
#include <cstdio>
#include <cctype>
#include <cstdlib>
#define MAXN 101inline int read() {int a = 0,f = 1;char v= getchar();while (!isdigit(v)) {if (v == '-') {f = -1;}v = getchar();}while (isdigit(v)) {a = a * 10 + v- 48;v = getchar();}return a * f;
}int pre[MAXN],ans;int main() {int n = read();for (int i = 1;i <= n;++i) {pre[i] = read();}for (int i = 2;i <= n;++i) {if (pre[i-2] == 3 && pre[i-1] == 1 && pre[i] == 2) {ans -= 1;}if (pre[i-1] == 1) {if (pre[i] == 2) {ans += 3;}else {ans += 4;}}if (pre[i-1] == 2) {if (pre[i] == 1) {ans += 3;}else {printf("Infinite");return 0;}}if (pre[i-1] == 3) {if (pre[i] == 1) {ans += 4;}else {printf("Infinite");return 0;}}}printf("Finite\n%d",ans);return 0;
}使用这份代码,你就可以快乐上分了






