2022 第47届沈阳站部分题解

F. Half Mixed

题面：

题目链接：F. Half Mixed

简要题意：
  给出 $n,m$， 求构造 $n$ 行 $m$ 列 只包含 $0,1$ 的数列,要求全部纯净块的数量 = 全部混合块的数量。纯净块指子矩形内所有数字要么全部是 $0$ ，要么全部是 $1$，而混合块则相反：子矩形内要包括$0,1$两种数字，问是否能构造出，若是能打印你所构造的序列。

解法思路：根据官方题解与自己理解结合而成

n 行的子矩形数量为 $\frac{n\ast (n+1)}{2}$
m行的子矩形数量为 $\frac{m\ast (m+1)}{2}$

如果$\frac{n\ast (n+1)}{2}\ast \frac{m\ast (m+1)}{2}$是奇数，那么永远构造不出来，始终会多出一个数，这个时候输入No即可.

若相乘是偶数，代表有解，假设 $\frac{m\ast (m+1)}{2}$ 是偶数，考虑 $1\times m$ 的情况，$1\times m$ 的子矩形有 $\frac{m\ast (m+1)}{2}$ ，设长度 $({\sum }_{i=1}^k{l}_1,l_2,\cdots ,l_k)=m$，每一个 $l_i$ 长度的子矩形数量为 $\frac{l_i\ast (l_i+1)}{2}$ ，纯净子矩形数量即为 ${\sum }_{i=1}^k\frac{l_i\ast (l_i+1)}{2}$，要满足纯净子矩形 $=$ 混合子矩形，则 ${\sum }_{i=1}^k\frac{l_i\ast (l_i+1)}{2}=\frac{m\ast (m+1)}{4}$ 且要满足 ${\sum }_{i=1}^k{l}_i=m$，其中 $\frac{m\ast (m+1)}{2}$ 代表 $m$ 列子矩形总数,要纯净和混合数量相同只需要两边各占一半，即纯子矩形数量满足 = $\frac{m\ast (m+1)}{4}$

每次选择尽可能大的 $l_i$ 的长度，二分 $mid$ 长度，找到最大满足 $\frac{mid\ast (mid+1)}{2}$ 大于等于 $need-(m-cnt)$ 的位置长度 $len$ ，将这段长度全部赋值相同的数，转换$01,flag=flag\oplus 1$ ， 然后减去这段区间产生的子矩形数量 $need-\frac{mid\ast (mid+1)}{2}$ ，直到 $need=0$，这个时候我们就构造出一个符合情况的序列了。

解释二分为什么是找大于等于 $need-(m-cnt)$ ，而不是直接找大于等于 $need$。
因为 m - cnt 代表剩下的位置需要 01 交替摆放，如果直接找大于等于 need，可能存在这个位置 mid 填了之后纯子矩形数量够了，但是没有满足构造出来长度和 = m 的情况

只要满足$1\times m$的情况，然后铺满$n$行也是满足要求的

代码块

#include<bits/stdc++.h>
using namespace std;#define ll long long
#define sc(x) scanf("%d",&x)
#define _sc(x) scanf("%lld",&x)
#define pf(x) printf("%d",x);
#define _pf(x) printf("%lld",x);
#define FOR(i,a,b) for(int i = a;i<=b;++i)
#define _FOR(i,a,b) for(int i = a;i<b;++i)
#define pb push_back
#define lb lowber_bound
#define ub upper_bound
#define lson(x) ((x) * 2)
#define rson(x) ((x) * 2 + 1)const ll mod = 1e9+7;
const ll maxn = 1e6+10;
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;ll pow2(ll a,ll n){ ll res = 1ll;while(n){if(n&1) res = (res*a)%mod;a = (a*a)%mod;n >>= 1;}return res;}ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; }int T;
ll n,m;
int a[maxn];
ll in[maxn];
void init(){in[1] = 1;for(int i = 2;i <= 1000000;++i){in[i] = in[i - 1] + i;} 
}
void calc(ll x){ll need = (x + 1) * x / 4;int cnt = 1 , flag = 1;while(need){/* 二分寻找最大的长度need - x + cnt ===> 所需要的 need 数量 - 还剩下(x - cnt)填补交替01形成的纯子矩形 */int pos = lower_bound(in + 1, in + 1 + 1000000 , need - (x - cnt)) - (in);for(int i = 1;i<=pos;++i){a[cnt++] = flag;}need -= in[pos];flag ^= 1;}
}void solve(){cin >> n >> m;ll sumN = (n + 1) * n / 2  , sumM = (m + 1) * m / 2;if((sumN & 1) && (sumM & 1)){cout << "No\n";return ;}cout << "Yes\n";int flag = 0;if(sumM & 1){swap(n,m);flag = 1;}calc(m);if(flag){for(int i = 1;i <= m;++i){for(int j = 1;j<=n;++j){cout << a[i] << " \n"[j == n];}}}else{for(int i = 1;i <= n;++i){for(int j = 1;j<= m;++j){cout << a[j] << " \n"[j == m];}}		}}
int main(void){std::ios::sync_with_stdio(0);std::cin.tie(0);init();cin >> T;while(T--){solve();}return 0;
} 

L. Tavern Chess

题面

题目描述

给定 $n$ 和 $m$ 分别代表Alice的团队士兵数量和鲍勃的团队士兵数量，现在两队的士兵进行攻击，若爱丽丝的士兵数量 $n>m$ ，则爱丽丝先手攻击鲍勃，如果是 $m>n$ 则鲍勃先手先攻击爱丽丝，如果 $n=m$ 则两边各 $50\%$的机会攻击对方。问最后爱丽丝赢得概率，鲍勃赢得概率，打平的概率。

攻击的规则如下：双方回合战，即每一轮攻击后交换攻击权，每次攻击由攻击次数最少且血量大于0的最左侧士兵攻击。士兵血量小于等于0视为死亡。

翻译巨坑：攻击次数最少的最左边士兵攻击

解法思路
观看范围 $n,m\le 7$ 可以第一时间判断爆搜，概率不均衡，所以直接带入概率进去算就完事了，
这题最坑在翻译攻击次数最少的士兵攻击这句话上。

代码块

#include<bits/stdc++.h>
using namespace std;#define ll long long
#define sc(x) scanf("%d",&x)
#define _sc(x) scanf("%lld",&x)
#define pf(x) printf("%d",x);
#define _pf(x) printf("%lld",x);
#define FOR(i,a,b) for(int i = a;i<=b;++i)
#define _FOR(i,a,b) for(int i = a;i<b;++i)
#define pb push_back
#define lb lowber_bound
#define ub upper_bound
#define lson(x) ((x) * 2)
#define rson(x) ((x) * 2 + 1)const ll mod = 1e9+7;
const ll maxn = 1e6+10;
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;ll pow2(ll a,ll n){ ll res = 1ll;while(n){if(n&1) res = (res*a)%mod;a = (a*a)%mod;n >>= 1;}return res;}ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; }int T;
ll n,m;ll a[8],b[8];
ll Aatk[8] , Batk[8];
ll AtkCnt[8] , BtkCnt[8];
double WinA , WinB , draw;int check(){int f1 = 1, f2 = 1;for (int i = 0; i < n; ++i){if (a[i] > 0){f1 = 0;break;}}for (int i = 0; i < m; ++i){if (b[i] > 0){f2 = 0;break;}}if(f1 && f2) return 2; // 打平局面if(f2) return 0;	//  A Winif(f1) return 1; // B Winreturn 3; // 还未完成的局面
}int Calc(int n , ll arr[8]){int res = 0;for (int i = 0; i < n; ++i){if(arr[i] <= 0) continue;++res;}return res;
}void dfs(auto a,auto b,int opt , double prob){int t = check();if(t != 3){if(t == 2) draw += prob;if(t == 0) WinA += prob;if(t == 1) WinB += prob;return ;}int size = Calc((opt == 0 ? m : n) , (opt == 0 ? b : a));double prob2 = prob / (1.0 * size);if(opt == 0){int pos , miCnt = 1e9+5;for (int i = 0; i < n; ++i){if(a[i] <= 0) continue;if(AtkCnt[i] < miCnt){miCnt = AtkCnt[i];pos = i;}}for(int i = 0;i<m;++i){if(b[i] <= 0) continue;b[i] -= Aatk[pos];a[pos] -= Batk[i];AtkCnt[pos]++;dfs(a,b,opt ^ 1,prob2);b[i] += Aatk[pos];a[pos] += Batk[i];AtkCnt[pos]--;			}}else{int pos , miCnt = 1e9+5;for (int i = 0; i < m; ++i){if(b[i] <= 0) continue;if(BtkCnt[i] < miCnt){miCnt = BtkCnt[i];pos = i;}}for(int i = 0;i<n;++i){if(a[i] <= 0) continue;a[i] -= Batk[pos];b[pos] -= Aatk[i];BtkCnt[pos]++;dfs(a,b,opt ^ 1,prob2);a[i] += Batk[pos];b[pos] += Aatk[i];BtkCnt[pos]--;		}}
}void solve(){cin >> n >>  m;for (int i = 0; i < n; ++i){cin >> a[i]; Aatk[i] = a[i];}for (int i = 0; i < m; ++i){cin >> b[i]; Batk[i] = b[i];}if(n > m){dfs(a,b,0,1);}else if(m > n){dfs(a,b,1,1);}else{dfs(a,b,0,0.5);dfs(a,b,1,0.5);}cout << fixed << setprecision(15) << WinA << "\n" << WinB << "\n" << draw << "\n";}
int main(void){std::ios::sync_with_stdio(false);std::cin.tie(0);T = 1;while(T--){solve();}return 0;
} 

C. Clamped Sequence

题面

题目描述

给定 $n$ 和 $d$ ，代表有 $n$ 个数，你可以选取一个区间 $[l,r]$ 要满足 $0\le r-l\le d$ ，问你选的区间 $[l,r]$ 后，按照题面那条公式更新数组的值 ，并且求得相邻两个数相减的绝对值最大。

解题思路
观察到范围 $n\le 5000$ ，直接就想到 $n^2$ 时间复杂度的解法。我们可以以每个数 $a_i$ 作为左端点 ，右端点即 $a_i+d$ ，然后 $O(n)$ 修改数组的值，加上两两差的绝对和取个最大值，最后还原数组。然后再以右端点 $a_i$，左端点 $a_i-d$ ，正反扫一遍取最大值即可。

代码块

#include<bits/stdc++.h>
using namespace std;#define ll long long
#define sc(x) scanf("%d",&x)
#define _sc(x) scanf("%lld",&x)
#define pf(x) printf("%d",x);
#define _pf(x) printf("%lld",x);
#define FOR(i,a,b) for(int i = a;i<=b;++i)
#define _FOR(i,a,b) for(int i = a;i<b;++i)
#define pb push_back
#define lb lowber_bound
#define ub upper_bound
#define lson(x) ((x) * 2)
#define rson(x) ((x) * 2 + 1)const ll mod = 1e9+7;
const ll maxn = 1e6+10;
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;ll pow2(ll a,ll n){ ll res = 1ll;while(n){if(n&1) res = (res*a)%mod;a = (a*a)%mod;n >>= 1;}return res;}ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; }int T;
ll n,m;ll a[5005] , b[5005];void solve(){ll d;cin >> n >> d;for (int i = 0; i < n; ++i){cin >> a[i]; b[i] = a[i];}ll ans = 0;for(int i = 0 ; i < n ;++i){int le = a[i] , ri = a[i] + d;for(int j = 0 ; j < n ; ++j){if(b[j] < le) b[j] = le;else if(b[j] > ri) b[j] = ri;}ll res = 0;for(int j = 0 ; j + 1< n ; ++j){res += abs(b[j] - b[j + 1]);b[j] = a[j];}b[n - 1] = a[n - 1];ans = max(res, ans);}for(int i = n - 1 ; i >= 0 ;--i){int le = a[i] - d , ri = a[i];for(int j = 0 ; j < n ; ++j){if(b[j] < le) b[j] = le;else if(b[j] > ri) b[j] = ri;}ll res = 0;for(int j = 0 ; j + 1< n ; ++j){res += abs(b[j] - b[j + 1]);b[j] = a[j];}b[n - 1] = a[n - 1];ans = max(res, ans);}	cout << ans << "\n";
}
int main(void){std::ios::sync_with_stdio(false);std::cin.tie(0);T = 1;while(T--){solve();}return 0;
} 

D. DRX vs. T1

题面

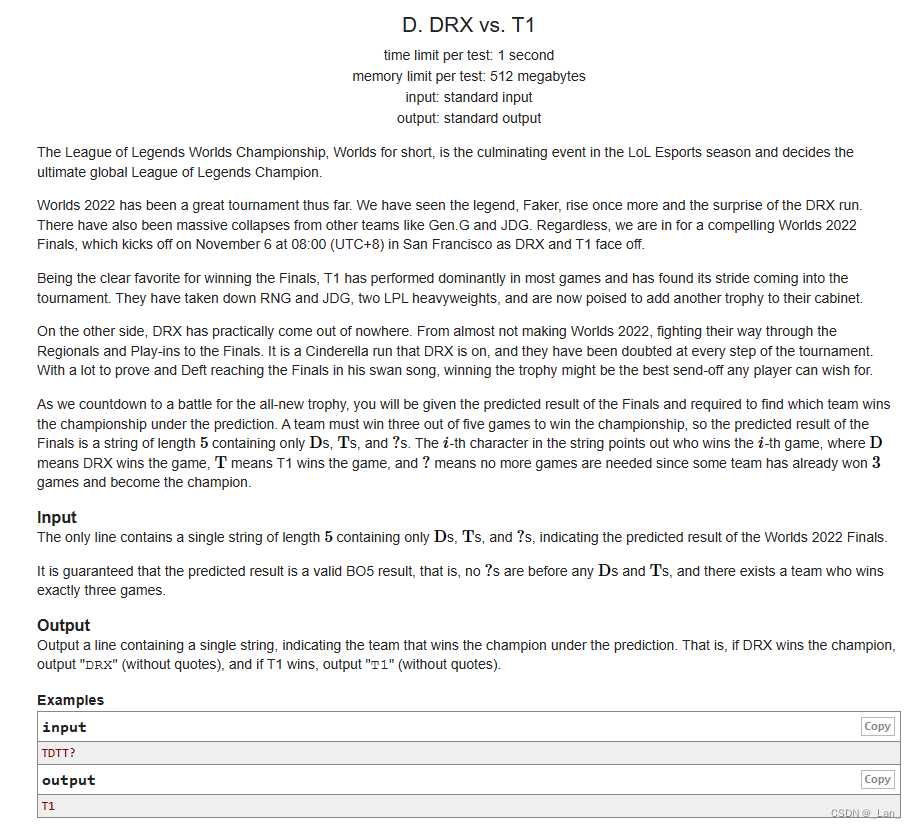
题目描述

福利签到题：就给出一行字符串，T出现次数多就输出T1，D出现次数多输出DRX

代码块

#include<bits/stdc++.h>
using namespace std;#define ll long long
#define sc(x) scanf("%d",&x)
#define _sc(x) scanf("%lld",&x)
#define pf(x) printf("%d",x);
#define _pf(x) printf("%lld",x);
#define FOR(i,a,b) for(int i = a;i<=b;++i)
#define _FOR(i,a,b) for(int i = a;i<b;++i)
#define pb push_back
#define lb lowber_bound
#define ub upper_bound
#define lson(x) ((x) * 2)
#define rson(x) ((x) * 2 + 1)const ll mod = 1e9+7;
const ll maxn = 1e6+10;
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;ll pow2(ll a,ll n){ ll res = 1ll;while(n){if(n&1) res = (res*a)%mod;a = (a*a)%mod;n >>= 1;}return res;}ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; }int T;
ll n,m;void solve(){string str;map<char,int> mp;cin >> str;for(auto x:str){mp[x]++;}if(mp['T'] > mp['D']) cout << "T1";else cout << "DRX";
}
int main(void){std::ios::sync_with_stdio(false);std::cin.tie(0);T = 1;while(T--){solve();}return 0;
} 

A想补，但是还没理解到位，先写这么多，下次再来