喷水装置（贪心 区间覆盖问题）

参考：[洛谷日报第74期]贪心讲解I_思路

第1部分 基础算法(提高篇)--第1章 贪心算法1424：【例题3】喷水装置_zqhf123的博客-CSDN博客

喷水装置

        长L米，宽W米的草坪里装有n个浇灌喷头。每个喷头都装在草坪中心线上（离两边各W/2米）。我们知道每个喷头的位置（离草坪中心线左端的距离），以及它能覆盖到的浇灌范围。 请问：如果要同时浇灌整块草坪，最少需要打开多少个喷头？

输入格式:

        输入包含若干组测试数据。

        第一行一个整数T表示数据组数。

        每组数据的第一行是整数n、L和W的值，其中n≤10 000。

        接下来的n行，每行包含两个整数，给出一个喷头的位置和浇灌半径。

        如下图所示的示意图是样例输入的第一组数据所描述的情况：

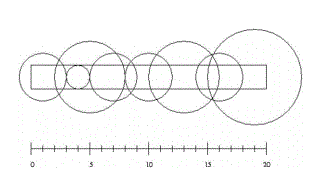
输出格式:

        对每组测试数据输出一个数字，表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开还不能浇灌整块草坪，则输出-1。

输入样例:

3
8 20 2
5 3
4 1
1 2
7 2
10 2
13 3
16 2
19 4
3 10 1
3 5
9 3
6 1
3 10 1
5 3
1 1
9 1

输出样例:

6
2
-1

参考代码如下：

#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
/*把圆换成长方形，就会发现它等价于有 n 个线段覆盖一个区间。-------区间覆盖问题。如何求圆所对应的线段两端点坐标？连接该圆心与该圆和草坪上方的两个交点，再取圆心到草坪上方的垂 线段，运用勾股定理即可求出。 接着将区间以左端点坐标为关键字从小到大排序。在当前龙头的右端点范围，找到下一个龙头能覆盖的最远的右端点。 
*/
int  T,n,l,w,pp,rr;
struct R
{double s;double e; 
}r[15005];
bool cmp(R a,R b)
{return a.s<b.s;
}
int main()
{while(cin>>T){while(T--){cin>>n>>l>>w;int cnt=0;for(int i=1;i<=n;i++){cin>>pp>>rr;if(rr>w/2.0){cnt++;//				将圆覆盖问题转化为长方形区间覆盖问题 r[cnt].s=pp-sqrt(rr*rr-w*w/4.0);r[cnt].e=pp+sqrt(rr*rr-w*w/4.0);;	}}sort(r+1,r+1+cnt,cmp);//			for(int i=1;i<=cnt;i++)
//			{
//				cout<<i<<" "<<r[i].s<<" "<<r[i].e<<endl;
//			}//		最远的右端点位置 double rpos=0;//		最少的使用个数 int res=0;//		喷头下标 int index=1;//		能否完全覆盖 bool isOk=true;
//			右端点小于右边距 while(rpos<l){
//				使用数+1 res++;
//				记录当前点的右端点 double cpos=rpos;
//			    在当前右端点cpos的范围内，喷头到右端点的最远距离 while(index<=cnt && r[index].s<=cpos ){
//					更新最远的右端点 if(rpos<r[index].e)rpos=r[index].e;
//					喷头向后使用 index++;}
//				若无法完全覆盖 if(rpos==cpos && cpos<l){cout<<"-1\n";isOk=false;break;}}if(isOk)cout<<res<<endl;}}  
}