学习《Statistical Learning》笔记

回归问题(Refression Problem)就是预测连续性或者数量型的输出的问题。比如根据你的年龄预测你的工资，当然可以增加多个输入，像性别、工龄、教育水平等等。

分类问题(Classfication Problem)就是预测结果落在哪个同中的问题。最简单的比如预测股票市场的上涨还是下跌。

聚类问题(Clustering Problem)就是将输入根据特称分为几类，不存在输出变量。

参数化方法(Parametric Methods)就是一种通过估计已经假设的函数中的参数，从而得到估计函数的方法。（往往带来很大的噪声）

非参数化(Non-parametric Methods)就是不假设模型/公式，而是通过定义一些到样本点的度量，来预测输出值。

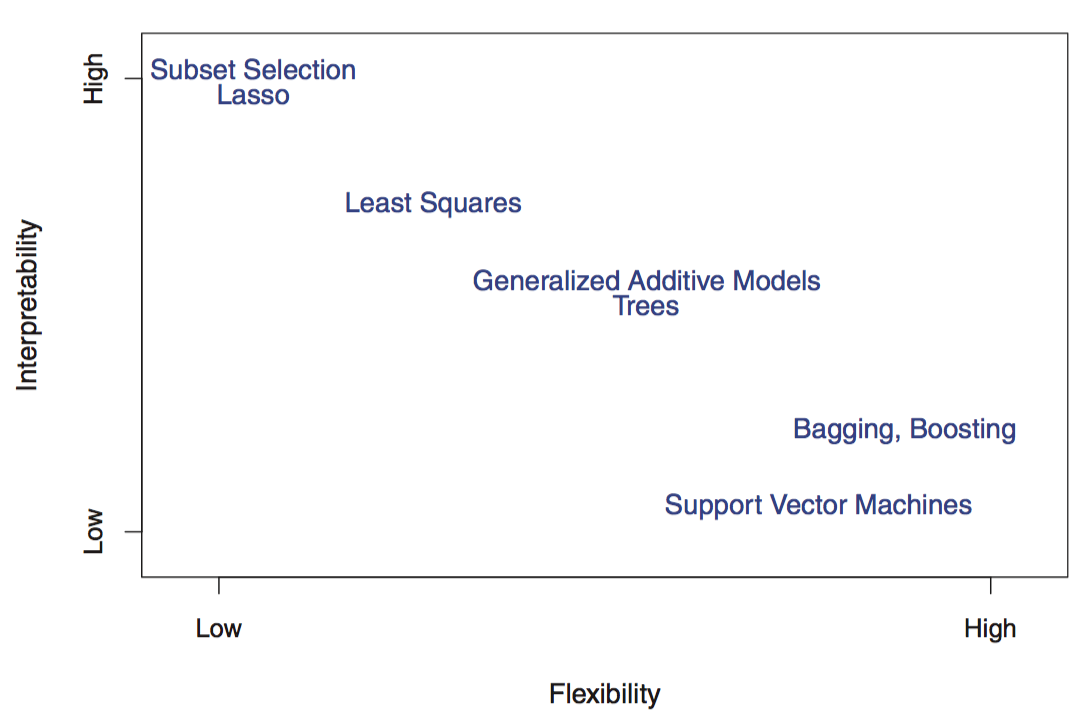
自由度(flexibility)越高的方法越难解释：不变量到变量，线性到非线性，都会导致自由度变高。

监督式学习(Supervised Learning)：对每一次观察/样本，都有响应的输出/响应与之对应，大部分的方法都是这种学习方法。

非监督式学习(Unsupervised Learning)：对应观察/样本，没有输出/响应，所做的学习是“盲“的，所以叫”非监督式学习”。比如”聚类(Clustering)”。

回归问题和分类问题区别在于数量性质和分类性质的问题。
MSE(Mean Squared Error)均方误差，公式定义如上，类似于数学期望的公式。

对于训练数据(training)来说，自由度增加，MES就会减少，但是对于验证数据(test)来说，自由度增加，MSE是一个U型曲线变哈化。

Overfitting：当采用方法时，对于training data会得出较小的MSE，但是对于test data，会得出很大的MSE的时候，这个方法就是overfitting的。

variance就是使用不同的训练数据，输出值的变化。一般来说，自由度越高，variance越大。

bias就是在建立的方法/模型/函数和实际的问题规律有偏差/错误，这个是建立的模型和真实的模型不同导致的。一般的，自由度越高，bias越小。

test error定义如上，就是用检验数据来衡量模型的准确度，输出值相等，test error不增加，输出值不等，对test error加权。对于分类模型来说，test error越小，模型越好。

贝叶斯模型是基于test error的思想，最小化test error，是一种分类模型。模型的关键，在于它是条件概率，也就是“限制某个变量固定值，其他变量随机取值(全体观察值)，计算得出输出值是某个值的概率/比率要达到最大“，换句话说，就是“限制某个变量为固定值，其他变量所有排列组合中，对应的输出值，在这些排列组合个体的数目最多，那这个观察值对应的“。
这里涉及到两个问题：如何根据原来的观察数据进行归类，从而分成多个桶，进一步的问题：桶的衡量标准是？我们要观察的的是一个条件概率，也就是一个变量不变，其他变量随机变化，导致的最终条件概率变化。怎么变化呢？可以是离散的、可以是分类的、可以是连续的，但是最终这个变化要拿去和我们要预测的test数据，去匹配，也就是test数据取临近值的时候，能落入这个桶内。这个匹配怎么操作？怎么算临近？也就是其他变量的随记变化如何度量？
我们可以认定它们是连续变化的，当test值取到临近区间的时候，就认为test数据落到了这个桶内。这个临近区间可以事先进行划分，而不是每一个样本都计算一遍，事先将连续变化的数值域划分成一个个区间，好比光谱的一个个频谱带。当test数据的某个分量的值，落在某个区间，就对应到那个桶内。

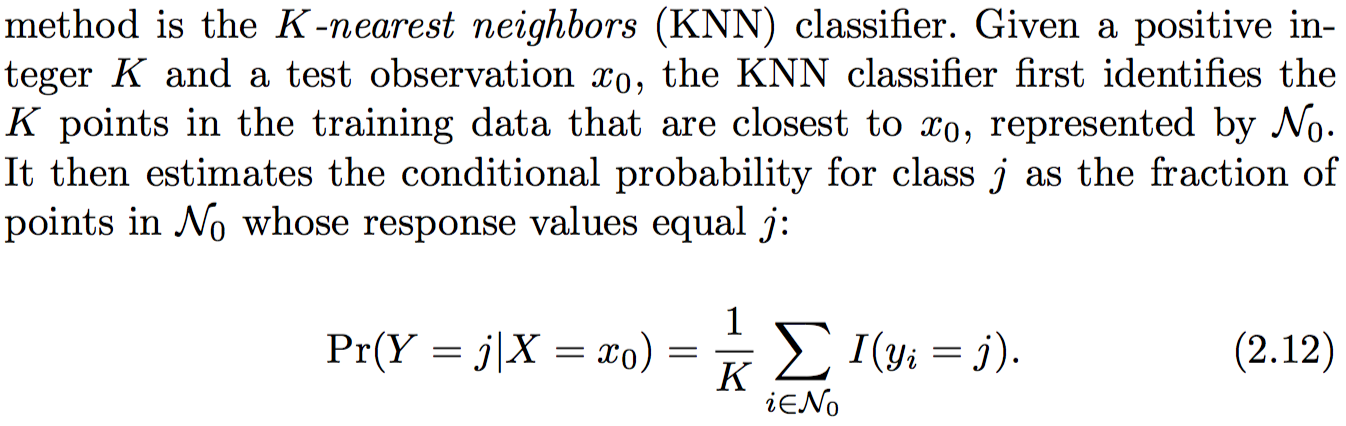
K临近算法，就是围绕test数据进行分析计算的一种方法，首先它通过实现确定的距离公式，计算得出距离test数据最近的K个观察点(观察数据)。然后再为每一个桶，计算条件概率，计算方法如上，关键就是K个点中，对应的桶占了几个点。如果要提前计算桶的衡量标准，也完全可以，就是对每一个test数据可能出现的点(数据实例)，都按照上面的方法事先计算一遍，确定这个实例所属的桶。在有新的test数据要预测输出的时候，只要把事先计算的桶返回就可以了。
(对variance和bias的影响：K值较小的时候，variance很大，但bias较小，K值较大的时候，variance很小，但bias较大，从而产生的预测都不好)

三种应用最广泛的分类器(模型/函数)：逻辑回归(logistic regression)、线性判别分析(linear discriminant analysis)和K临近分析(K-nearest neighbors)。计算机增强型(computer-intensive)方法：广义可加模型(generalized additive models)，树形(trees)，随即森林(random forests)，support vector machines(支持向量机)。
最大似然估计：假设既定的数据模型，围绕出现的样本，衡量模型的参数指标，让这个样本出现的可能性最大。
（定义很晦涩，简单理解下：比如这个数据模型：，是给定参数：每次出现的概率w=0.2，计算10次出现的次数的概率，y是出现的次数。如果我们不知道参数，只知道出现了y次，比如y=4或者y=6，怎么估计w?很显然这个模型就是很好的估计方式，我们让w取一个值，使得这个模型计算出来的概率是最大的，反过来，这个w值也应该是最可能的，也就是说这个模型成为了衡量它自身指标的指标。如果w有多个分量，比如w1\w2\w3等等，注意，最终公式的自变量还是x，只不过x的取特定的样本值，所以无法进行相乘，作为联合概率密度来处理。对应的衡量公式中，w各个分量会同时出现，所以求最大值时，是对w的多个分量求偏导的。
但是，如果我们拿到了x的多个样本值，这些样本值又是相互独立的，那么我们在构造所谓的衡量模型的时候，就可以用相互独立的x样本值，来构造联合概率密度，让联合概率密度的值最大，从而选出最可能的w参数值。从而，我们的概率密度公式是这样： 这里样本x的下标是变化的。
）