BZOJ2321 [BeiJing2011集训]星器 能量守恒定律

题目大意：在一个二位矩阵上有一些星器，把两个不相邻的星器互相靠近一格会产生两个星器距离的能量，给出始末状态，求产生的最大能量。

以前偶然间看过这道题的题解，用到了能量守恒定律
在neither_nor看这道题的时候我告诉他这道题是物理以后我就滚回去看了题解…
他自己推出来了一个和网上都不一样的做法，果然是神犇，%%%

可以把两个星器的移动以后产生的能量看成是移动消耗的能量，这样根据能量守恒，计算出始末状态的能量差即为答案

势能是相对的，可以定义一个星器相对于原点的势能为横纵坐标的平方和的一半。
验证一下势能的定义是否正确。横纵坐标两项相互独立，互不影响。这样这里只对于一维坐标计算。设移动前 两个星器的坐标分别为x,y，移动后分别为(x+1),(y-1)，势能差为

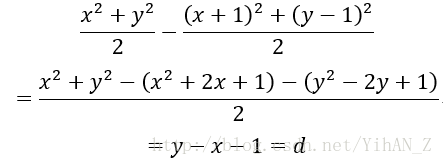
恰好为释放的能量。

若将势能定义为一次多项式，则消耗的能量与移动次数有关；若将势能定义为二次多项式，则消耗的能量与距离有关。

#include <cstdio>
#define N 205
using namespace std;
typedef long long LL;
inline LL sq(int x) { return x*x; }
int n,m,tmp,a[N][N];
LL sum;
int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&tmp),sum+=(LL)(a[i][j]-tmp)*(sq(i)+sq(j));printf("%lld\n",sum/2);return 0;
}