2022暑初二信息竞赛学习笔记集锦

Day 3：新知——并查集

学习笔记

一、概念

1. 概念：用来表示不相交集合的数据结构，处理不相交集合的合并和查询问题。每个集合通过代表来区分。
2. 操作：
   (1) FindSet (x)
   用来查找元素 x 属于哪个集合，返回集合的代表。
   (2) UnionSet (x, y)
   如果 x 、 y 属于不同集合，则将 x 、 y 所在集合进行合并，否则不进行任何操作/
3. 实现方法：有根树表示集合。

二、基本操作

1. 初始化 MakeSet
   用father[i]表示i的父结点。

void MakeSet () {for (int i = 1; i <= n; i ++) {father[i] = i;//若父节点与自己相同，则为根结点。}
}

2. 查询 FindSet

int FindSet (int x) {if (father[x] == x) {//同上注释return x;} else {return FindSet (father[x]);}
}

3. 合并 UnionSet

void UnionSet () {if (FindSet (x) == FindSet (y)) {//如果x、y在同一集合，不用合并。return;}father[FindSet (x)] = FindSet[y];//接在y的根结点上。
}

三、并查集优化1——路径压缩

int FindSet (int x) {if (father[x] == x) {//同上注释return x;} else {return father[x] = FindSet (father[x]);//直接连到根结点。}
}

四、并查集优化2——按秩合并(启发式合并)

用rank[i]维护以i结点为根的子树的深度。

void UnionSet () {int a = FindSet (x), b = FindSet (y);if (a == b) {//如果x、y在同一集合，不用合并。return;}if (rank[a] <= rank[b]) {//如果b树比a树深，把a接在b后father[a] = b;} else {//否则把b接在a后father[b] = a;}if (rank[a] == rank[b]) {//如果a和b一样深，根据刚才的语句是接在b后的，则b的深度要加1rank[b] ++;}
}

五、带权并查集(边带权并查集)

六、种类并查集(扩展域并查集)

Day 5：新知——树状数组

学习笔记

一、概念

树状数组(Binary Indexed Tree，简称BIT)，是一个区间查询和单点修改时间复杂度降为$\Theta (\log n)$的数据结构，主要用于查询任意两点之间所有元素之和。

二、问题的提出

一个一维数组，长度为$n$，接下来要对这个数组进行两种操作：

• 修改，对$i$~$j$之间的元素增加$x$；
• 求和，求第$i$个元素到第$j$个元素的和。

三、解决办法

办法一：前缀和

优点：求和：$\Theta (1)$。
缺点：修改：$\Theta (n)$。

办法二：树状数组

重点:lowbit (x)函数

求把$x$转化成二进制后，取末尾的$1$和后面的$0$，再转化成十进制的值。

写法：

int lowbit (int x) {return x & -x;
}

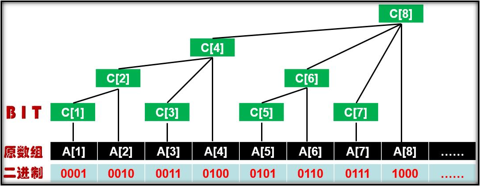
bit[i]数组就是上图中的C[i]数组，按照上图规律：

bit[1] = a[1]
bit[2] = bit[1] + a[2]
bit[3] = a[3]
bit[4] = bit[2] + bit[3] + a[4]
...

重点:update (k, x)函数：将第k个元素的值加x。

void update (int k, int x) {for (int i = k; i <= n; i += lowbit (i)) {//由上图易得，第i个元素+lowbit (i)即为它的上级元素bit[i] += x;}
}

重点:sum (k)函数：求第k个元素的值。

int sum (int k) {int ans = 0;for (int i = k; i > 0; i -= lowbit (i)) {//累加差分(bit)数组即为原数ans += bit[i];}return ans;
}

四、离散化

Q：为什么要离散化？
A：在某些时刻，数据较大时且只需知道元素的位置而元素的值无关紧要时，可以使用离散化来简化数据的强度。

离散化方法一：用数组进行离散化

struct node {int val, id;bool operator < (const node x) const {return val < x.val;}
}
......
for (int i = 1; i <= n; i ++) {scanf ("%d", &a[i].val);a[i].id = i;
}
sort (a + 1, a + n + 1);
b[a[i].id] = i;

离散化方法二：用STL+二分离散化

#include <algorithm>
using namespace std;int a[MAXN], lsh[MAXN], cnt, n;
......
for (int i = 1; i <= n; i ++) {scanf ("%d", &a[i]);lsh[i] = a[i];
}
sort (lsh + 1, lsh + n + 1);//排序
cnt = unique (lsh + 1, lsh + n + 1) - lsh - 1;//去重
for (int i = 1; i <= n; i ++) {a[i] = lower_bound (lsh + 1, lsh + cnt + 1, a[i]) - lsh;//返回坐标
}

Day 8：新知——哈希Hash表

学习笔记

一、Hash函数

指可以根据关键字直接计算出元素所在位置的函数。

二、哈希表

根据设定的哈希函数 Hash(key) 和处理冲突的方法将一组关键字映象到一个有限的连续的地址集（区间）上，并以关键字在地址集中的 “象” 作为记录在表中的存储位置，这种表便称为哈希表，这一映象过程称为哈希造表或散列，所得存储位置称为哈希地址或散列地址。

三、冲突

1. 定义：不同的元素占用同一个地址的情况叫做冲突。
2. 发生冲突的因素
   (1) 装填因子$\alpha$
   装填因子是指哈希表中己存入的元素个数 $n$ 与哈希表的大小 $m$ 的比值，即$\alpha =\frac{n}{m}$。$\alpha$越小，发生冲突的可能性越小，反之，发生冲突的可能性就越大。但是，$\alpha$太小又会造成大量存贮空间的浪费，因此必须兼顾存储空间和冲突两个方面。
   (2)所构造的哈希函数
   构造好的哈希函数，使冲突尽可能的少。
   (3)解决冲突的方法
   设计有效解决冲突的方法 。.

四、Hash函数的构造方法

1. 直接定址法
   取关键字或关键字的某个线性函数值为散列地址，即Hash(K)=K 或 Hash(K)=a * K + b（其中$a$、$b$为常数）。
   优点：以关键码 key 的某个线性函数值为哈希地址，不会产生冲突。
   缺点：要占用连续地址空间，空间效率低。

2. 除后余数法 (常用)
   取关键字被不大于散列表表长 $m$ 的数 $p$ 除后所得的余数为哈希函数。即
   $Hash(K)=K\mathrm{mod}p(p\le m)$

   ps：经验得知，一般可选$p$为质数 或 不包含小于$20$的质因子的合数。例如：131, 1331, 13331, ...

3. 平方取中法
   取关键字平方后的中间几位为哈希函数。因为中间几位与数据的每一位都相关。
   例：$2589$的平方值为$6702921$，可以取中间的$029$为地址。

4. 数字分析法
   选用关键字的某几位组合成哈希地址。
   选用原则应当是：各种符号在该位上出现的频率大致相同。

5. 折叠法
   是将关键字按要求的长度分成位数相等的几段，最后一段如不够长可以短些，然后把各段重叠在一起相加并去掉进位，以所得的和作为地址。
   适用于：每一位上各符号出现概率大致相同的情况。
   具体方法：
   移位法：将各部分的最后一位对齐相加（右对齐）。
   间接叠加法：从一端向另一端沿分割界来回折叠后，最后一位对齐相加。
   例：元素$42751896$,
   移位法： $427＋518＋96=1041$
   间接叠加法： $42751896->724+518+69=1311$

6. 随机数法
   选择一个随机函数，取关键字的随机函数值为它的哈希地址，即Hash (key) = random (key) 其中random为随机函数(random是C语言函数)。
   通常，当关键字长度不等时采用此法构造哈希函数较恰当。
   rand (): 取随机数，以默认种子1来生成，只要种子一样，无论何时何地生成的随机数都一样。
   srand (x): 将随机数的种子改为$x$。
   time (0): 获取当前时间，因为时间一直在变化，所以随机数的值也在变化。
   参考代码：

#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;int main () {srand (time (0));printf ("%d\n", rand ());return 0;
}

7. 建立Hash ()函数通常考虑的因素
   (1)计算哈希函数所需时间(包括硬件指令的因素)；
   (2)关键字的长度；
   (3)哈希表的大小；
   (4)关键字的分布情况；
   (5)记录的查找频率。

五、处理冲突的办法

1. 开放地址法
   开放地址就是表中尚未被占用的地址，当新插入的记录所选地址已被占用时，即转而寻找其它尚开放的地址。
   (1) 线性探测法
   设散列函数 Hash (K) = K mod m （$m$为表长），若发生冲突，则沿着一个探查序列逐个探查(也就是加上一个增量)，那么，第i次计算冲突的散列地址为：
   $$H_i=(H(K)+d_i)\mathrm{mod}m(d_i=1,2,\dots ,m-1)$$
   优点：只要哈希表未被填满，保证能找到一个空地址单元存放有冲突的元素；
   缺点：可能使第$i$个哈希地址的同义词存入第$i+1$ 个哈希地址，这样本应存入第$i+1$个哈希地
   址的元素变成了第$i+2$个哈希地址的同义词，……，因此，可能出现很多元素在相邻的哈希
   地址上“堆积”起来，大大降低了查找效率。
   (2) 二次探测法
   二次探测法对应的探查地址序列的计算公式为：
   $$H_i=(H(k)+d_i)\mathrm{mod}m$$
   其中$d_i=1^2,-1^2,2^2,-2^2,\dots ,j^2,-j^2(j\le m/2)$。

2. 链地址法
   基本思想：
   将具有相同哈希地址的记录链成一个单链表，m个哈希地址就设 m个单链表，然后用一个数组将m个单链表的表头指针存储起来，形成一个动态的结构。
   优点：插入、删除方便。
   缺点：占用存储空间多。

3. 再哈希法
   基本思想：

$$H_i=R{H}_i(key)(i=1,2,3,\dots \dots ,k)。$$

其中，$R{H}_i()$ 均是不同的哈希函数，即在同义词产生地址冲突时计算另一个哈希函数地址，直到冲突不再发生。
优点：不易产生“聚集”。
缺点：增加了计算时间。

4. 建立一个公共溢出区
   基本思想：
   假设哈希函数的值域为$[0,m-1]$，则设向量$HashTable[0,m-1]$为基本表。在此基础上，再建立一个溢出表，在之后的哈希操作中，无论关键字的同义词生成怎样的哈希地址，一旦发生冲突，就将其放入溢出表中。

Day 10：新知——图的概念、结构和遍历

学习笔记

一、定义

图(graph)，用来存储某些具体事物和这些事物中的联系。
图由顶点(vertex)——具体事物和边(edge)——联系组成
顶点集合为$V$，边的集合为$E$，图表示为$G=(V,E)$

二、种类

1. 无向图：边没有指定方向的图。
2. 有向图：边具有指定方向的图。
   注：有向图所连的边也叫做弧，一条边起点为弧头，终点为弧尾。
3. 带权图：边上带有权值的图。

三、无向图的术语

1. 两个顶点之间有边连接，则称两个顶点相邻。
2. 路径：相邻顶点的序列。
3. 圈：起点与终点重合的路径。
4. 度：顶点连接边的条数。
5. 树：没有圈的连通图。
6. 森林：没有圈的非连通图。

四、有向图的术语

1. 在有向图中，边是单向的，它们的邻接性是单向的。
2. 有向路径：相邻顶点的序列。
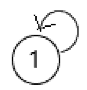
3. 有向环：一条至少含有一条边且起点和终点相同的路径。特别地，自环(见下图)
   
4. 有向无环图(DAG)：没有环的有向图。
5. 度：一个顶点的出度和入度之和即为该顶点的度。
   (1) 入度：以顶点为弧尾的边的数量。
   (2) 出度：以顶点为弧头的边的数量。

五、图的表示

1. 邻接矩阵
   对于一个有$V$个顶点的图而言，使用$V\times V$的二维矩阵表示
   $G_{i,j}=1$，有边相连
   $G_{i,j}=0$，无边相连
   无向图：$G_{i,j}=G_{j,i}=1$
   优点：可以用常数时间判断是否有边存在
   缺点：表示稀疏图时，浪费大量空间。

2. 邻接表
   用一个不定长数组vector存储G[i]表示与i边有相连的序列。

3. 链式前向星
   用几个数组来维护边之间的特殊关系。

六、图的遍历

1. DFS(深度优先搜索)
   
2. BFS(广度优先搜索)
   

Day 11：新知——最短路

学习笔记

一、概念

最短路径问题就是寻找图中两节点之间的最短路径。

二、Floyd算法

Floyd算法是最简单的最短路径算法，可以计算图中任意两点间的最短路径，但是时间复杂度和空间复杂度极高：$\Theta (n^3)$，且适用于负边权。

1. 初始化
   定义一个数组f[i][j]，表示i点到j点的最短路。
   伪代码：
   $memset(f,inf)$
   $f_{i,i}=0$
   有边相连：$f_{u,v}=w_{u,v}$
   无边相连：$f_{u,v}=inf$

2. 算法

void floyd () {for (int k = 1; k <= n; k ++) {for (int i = 1; i <= n; i ++) {for (int j = 1; j <= n; j ++) {f[i][j] = min (f[i][j], f[i][k] + f[k][j]);}}}
}

算法本质	DP
阶段	第$i$个点经过前$k$个点中任意若干个点到第$j$个点
状态转移方程	$f_{k,i,j}=\min (f_{k-1,i,j},f_{k-1,i,k}+f_{k-1,k,j})$
状态转移方程(省去$k$维)	$\min (f_{i,j},f_{i,k}+f_{k,j})$

3. 记录路径
   定义pre[i][j]表示从i到j的路径中j的前驱。

• 初始化：$pr{e}_{i,j}=i$(在无向图中$pr{e}_{j,i}=j$)
• 更新：$pr{e}_{i,j}=pr{e}_{k,j}$

三、Dijkstra算法

把结点分成两组：已经确定最短路的结点，尚未确定最短路的结点。
我们不断从第2组中的结点放入第1组并扩展。
本质是贪心，只能应用于正权图。
普通Dijkstra算法的时间复杂度为$\Theta (O^2)$，小根堆优化后时间复杂度为$\Theta (\log n)$~$\Theta (\log m)$

1. 松弛
   做一个形象的比喻，原来用一根橡皮筋直接连接$a$、$b$两点，若有一点$k$使得$a\to k\to b$比$a\to b$更短，则改成$a\to k\to b$，让橡皮筋更松弛。

代码

if (dis[b] > dis[k] + w[k][b]) {dis[b] = dis[k] + w[k][b];
}

2. 初始化
   我们设起点为$s$，终点为$e$，dis[v]表示从指定$s$到$v$的最短路，pre[v]表示$v$的前驱，用来输出路径。
   伪代码：
   $memset(dis,+\infty )$
   $memset(vis,0)$
   $for(i:1$~$n)\to di{s}_i=w_{s,i}$
   $di{s}_0=pr{e}_s=0,vi{s}_s=1$

3. 算法

$for(i:1$~$n-1)$
(1) 在所有未标记的点中找出$dis$最小的$k$
(2) 标记$k$
(3)松弛从$k$出发的边

void dijkstra () {memset (dis, 0x3f, sizeof dis);memset (vis, 0, sizeof vis);for (int i = 1; i <= n; i ++) {dis[i] = w[s][i];}dis[0] = pre[s] = 0, vis[s] = 1;for (int i = 1; i <= n - 1; i ++) {int k = -1, minn = 0x3f3f3f3f;for (int j = 1; j <= n; j ++) {if (dis[j] < minn) {k = j, minn = dis[j];}}if (vis[k] == 1) {continue;}vis[k] = 1;for (int i = 1; i <= n; i ++) {if (w[i][k] != 0X3f3f3f3f) {if (dis[i] > dis[k] + w[k][i]) {dis[i] = dis[k] + w[k][i];} }}}
}

4. Dijkstra算法堆优化(小根堆)

(1) 找出$dis$最小的$k$，我们可以用priority_queue优先队列来完成(优化第一个小循环)
(2) 用邻接表或链式前向星拉出与$k$相邻的边的序列(优化第二个小循环)

priority_queue <pair <int, int> > q;void dijkstra () {while (q.size()) {q.pop();}memset (dis, 0x3f, sizeof dis);dis[s] = 0;q.push(make_pair (0, s));while (q.size()) {int t = q.top().second;q.pop();if (vis[t] == 1) {continue;}vis[t] = 1;for (int i = head[t]; i; i = next[i]) {int x = to[i], y = w[i];if (dis[x] > dis[t] + y) {dis[x] = dis[t] + y;q.push(make_pair (-dis[x], x));}}}
}

Day 12：新知——最短路

学习笔记

四、Bellman-Ford算法

对每条边执行更新，迭代$N-1$次。具体操作是对图进行最多$n-1$次松弛操作，每次操作对所有的边进行松弛，可以应用于有向负权图。

1. 初始化

伪代码：

$memset(dis,\infty ),di{s}_s=0,pr{e}_s=0$

2. 算法

void relax (int x, int y, int w) {if (dis[y] > dis[x] + w) {dis[y] = dis[x] + w;}
}for (int i = 1; i <= n - 1; i ++) {for (int j = 1; j <= m; j ++) {relax (edge[j].s, edge[j].e, edge[j].w);}
}

在$n-1$次操作中，枚举每一条边是否能被松弛(relax操作)即可。

3. 判断负环

(1)负环的概念：权值为负数的有向环即为负环。

(2)在Bellman_Ford算法中判断负环：

观察下图：

负环都满足以下性质：
$$di{s}_s+w<di{s}_e$$
所以，我们再用一重循环，若满足这个性质，一定出现负环。

void relax (int x, int y, int w) {if (dis[y] > dis[x] + w) {dis[y] = dis[x] + w;}
}bool bellman_ford () {memset (dis, 0x3f, sizeof dis);dis[s] = 0;for (int i = 1; i <= n - 1; i ++) {for (int j = 1; j <= m; j ++) {relax (edge[j].s, edge[j].e, edge[j].w);}}for (int i = 1; i <= m; i ++) {if (dis[edge[i].s] + edge[i].w < dis[edge[i].e]) {return 0;}}return 1;
}

五、SPFA算法

SPFA算法，即用队列优化的Bellman-Ford算法，本质上还是迭代——每更新一次就考虑入队。

可以应用于有向负权图。

时间复杂度：稀疏图上$\Theta (kN)$，稠密图上退化到$\Theta (N^2)$

1. 算法实现

在Bellman-Ford算法中，有许多松弛是无效的。这给了我们很大的改进的空间。SPFA算法正是对Bellman-Ford算法的改进。它是由西南交通大学段丁凡1994年提出的。它采用了队列和松弛技术。先将源点加入队列。然后从队列中取出一个点(此时该点为源点)，对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径。

2. 判断有无负环：如果某个点进入队列的次数超过$N$次则存在负环 ( 存在负环则无最短路径,如果有负环则会无限松弛,而一个带$n$个点的图至多松弛$n-1$次)

void spfa (int s) {memset (dis, 0x3f, sizeof dis);memset (vis, 0, sizeof vis);memset (c, 0, sizeof c);//c数组来判断进入队列的次数queue <int> q;dis[s] = 0, vis[s] = 1, c[s] = 1; q.push(s);while (q.size()) {int t = q.front();q.pop();vis[t] = 0;for (int i = head[t]; i; i = next[i]) {int x = to[i], y = w[i];if (dis[x] > dis[t] + y) {dis[x] = dis[t] + y;c[x] = c[t] + 1;if (c[x] == n) {printf ("-1");exit (0);}if (vis[x] != 1) {q.push(x);vis[x] = 1;}}}}
}

Day 14：新知——最小生成树

学习笔记

一、最小生成树

1. 生成树：个点用$N-1$条边连接成一个连通块，形成的图形只可能是树，叫做生成树。因此，一个有N个点的连通图，边一定$\ge N-1$条。
2. 最小生成树(Minimum Spanning Trees，MST)：求无向带权图的一棵子树，包含$N$个点，$N-1$条边，边权之和最小。

二、Prim算法

以任意一个点为基准点，节点分为两组：

(1) 在MST上到基准点的路径已经确定的点

(2) 尚未在MST中与基准点相连的点

不断从第$2$组中选择与第$1$组距离最近的点加入第$1$组，类似于Dijkstra算法，本质也是贪心，时间复杂度为$\Theta (n^2)$。

1. 总体思想：像Dijkstra一样，也使用“蓝白点”思想，白点代表已进入最小生成树的点，蓝点代表未进入最小生成树的点。以$1$为起点生成最小生成树，d[v]表示蓝点$v$与白点相连的最小边权，mst表示最小生成树的权值之和。
2. 初始化

伪代码：

$memset(d,\infty ),d_1=0,mst=0$

3. 算法

$for(i:1$~$n-1)$

(1) 寻找d最小的x，并将其标记。

(2) 累加答案mst += d[x];

(3) 再将与$x$相邻的点更新d[x]的值。

算法结束，mst即为最小生成树的权值之和。

4. Prim算法堆优化(小根堆)

(1) 找出$dis$最小的$k$，我们可以用priority_queue优先队列来完成(优化第一个小循环)
(2) 用邻接表或链式前向星拉出与$k$相邻的边的序列(优化第二个小循环)

其实跟Dijkstra算法的优化是一样一样的啦。

void prim () {for (int i = 1; i <= n; i ++) {d[i] = inf, vis[i] = 0;}d[1] = 0;q.push(make_pair (0, 1));while (q.size()) {int t = q.top().second;q.pop();if (vis[t] == 1) {continue;}vis[t] = 1;for (int i = head[t]; i; i = next[i]) {int x = to[i], y = w[i];if (vis[x] == 0 && d[x] > y) {d[x] = y;q.push(make_pair (-d[x], x));}}mst += d[t];}
}

三、Kruskal算法

利用并查集，起初每个点各自构成一个集合，所有边按照边权从小到大排序，依次扫描。

若当前扫描到的边连接两个不同的点集就合并，本质也是贪心，时间复杂度为$\Theta (M\log N)$。

与Prim算法相比，没有基准点，该算法是不断选择两个距离最近的集合进行合并的过程。

1. 初始化

用cnt表示已经连的边数。

$sort(ed,cmp\to$按照边权排序$)$

$mst=0,cnt=0$

2. 算法

$for(i:1$~$m)$

(1) 如果两个点不在同一个集合，合并，mst += 边权;

(2) 如果cnt连了$n$条边了，跳出算法。

struct node {long long u, v, w;bool operator < (const node x) const {return this->w < x.w;}
} ed[MAXN];void MakeSet () {for (int i = 1; i <= n; i ++) {father[i] = i;}
}int FindSet (int x) {if (x == father[x]) {return x;} else {return father[x] = FindSet (father[x]);}
}bool UnionSet (int x, int y, int i) {int a = FindSet (x), b = FindSet (y);if (a == b) {return 0;}father[a] = b;cnt ++;mst += ed[i].w;return 1;
}void kruskal () {sort (ed + 1, ed + m + 1);for (int i = 1; i <= m; i ++) {if (UnionSet (ed[i].u, ed[i].v, i) == 0) {continue;}if (cnt == n) {return;}}
}

Day 22：新知——倍增&RMQ算法

学习笔记

一、倍增算法概述

倍增，顾名思义就是查找的范围按照翻倍而扩大或缩小，从而达到加速计算的效果。

举一个例子，假设你站在$0$点，你需要跳到$15$个单位长度的地方。

如果每一次都只跳$1$个单位长度，那么需要跳$15$次。

如果按照倍增的思路，那么只需要跳$4$次就可以达到$15$:

设距离终点的长度为$d$，那么我们每次都可以找到一个数$k$，使得$2^k\le d$且$k$最大的值，就在这时，我们向前跳$2^k$个单位长度，就是最优的跳跃长度。

• 第一步，$d=15$，$\because 2^3\le 15$，$\therefore$ 求得$k=3$，跳$8$个单位长度。

• 第二步，$d=7$，$\because 2^2\le 7$，$\therefore$ 求得$k=2$，跳$4$个单位长度。

• 第三步，$d=3$，$\because 2^1\le 3$，$\therefore$ 求得$k=1$，跳$2$个单位长度。

• 第四步，$d=1$，$\because 2^0\le 1$，$\therefore$ 求得$k=0$，跳$1$个单位长度。

这时，$d=0$，结束跳跃，所以只需要跳$4$步。

二、RMQ算法

RMQ (Range Minimum/Maximum Query)，即区间最值算法。

作用：对于 ∀ l , r ∈ { 1 , 2 , . . . , n } \forall l,r \in \{1,2,...,n\} ∀l,r∈{1,2,...,n} 且 $l\le r$，都可以以$\Theta (1)$的时间复杂度，求到 max ⁡ i = l r { a i } \max_{i=l}^r\{a_i\} maxi=lr​{ai​}。

算法原理：

1. 预处理部分

我们定义一个数组rmq[i][j]，类似于定义一个DP数组，表示从第$i$个元素开始往后数$2^j$个元素中的最大值。

首先我们可以很简单的预处理一下：$rm{q}_{i,i}=a_i$。

很简单的道理，在一个数里选极值，肯定就是这个数。

接下来用一个dp进行状态转移，状态转移方程为：(此处以求最大值为例)
r m q i , j = max ⁡ { r m q i , j − 1 , r m q i + 2 j − 1 , j − 1 } rmq_{i,j}=\max\{rmq_{i,j-1},rmq_{i+2^{j-1},j-1}\} rmqi,j​=max{rmqi,j−1​,rmqi+2j−1,j−1​}
这个状态转移方程也很好理解，就是将整串数对半分，左侧极值和右侧极值更加极端的值就是整串数的极值。

for (int j = 1; (1 << j) <= n; j ++) {for (int i = 1; i + (1 << j) - 1 <= n; i ++) {rmq[i][j] = max (rmq[i][j - 1], rmq[i + (1 << j - 1)][j - 1]);}
}

这样，我们就以$\Theta (n\log n)$的时间复杂度求得了$rmq$数组，$10^6$的数据不在话下。

最后，要求$l$和$r$之间的极值$(l\le r)$，当然是不能直接输出$rm{q}_{l,r}$的。

我们可以求到一个值$k$，使得从$l$出发的右$2^k$个数中的极值，和$r$出发的左$2^k$个数中的极值两个数中极值就是$l$到$r$的极值。

所以，我们只要保证$r-2^k+1\le l+2^k-1$成立即可。

$r-2^k+1\le l+2^k-1$

移项得：$r-l+2\le 2^{k+1}\cdots \cdots ①$

$\because l\le r$ (前提条件)

$\therefore 0\le r-l$

$\therefore r-l\le 2(r-l)$

$\therefore r-l+2\le 2(r-l+1)\cdots \cdots ②$

现在观察$①$、$②$两式，其左侧相同，右侧一个只带有$k$，一个只带有$l$或$r$，我们就可以认为$2(r-l+1)=2^{k+1}$，从而求出$k$的值。

再次化简，得$k={\log }_2(r-l+1)$，这就是$k$的计算公式。

int getrmq (int l, int r) {int k = log2 (r - l + 1);return max (rmq[l][k], rmq[r - (1 << k) + 1][k]);
}

RMQ算法就是典型的倍增思想解题。RMQ算法又称**ST算法**，其中rmq数组又称**ST表**。

Day 24：新知——拓扑排序&关键路径

学习笔记

一、拓扑排序的定义

拓扑排序，是一个只适用于$AOV$网的算法。$AOV$网，即$DAG$(有向无环图)。对于一个$DAG$进行拓扑排序，是将整个图$G$的所有顶点排序成一个线性序列，使得图$G$中的任意一对顶点$u$和$v$，若边$<u,v>\in E(G)$，则$u$在这个序列中出现在$v$之前。这样的序列称为满足拓扑次序(Topological Order)的序列，注：拓扑排序的序列在一些情况中不唯一，也有可能无解。

二、拓扑排序问题的解决

思想：

1. 首先选择一个**入度为$0$**的点。
2. 从$AOV$网($DAG$)中，删除此顶点以及与之相连的边。
3. 重复以上步骤，直到不存在入度为$0$的点。
4. 如果选择的点数小于总点数，说明图中有环或孤岛;若选择的点数等于总点数，那么顶点选择的次序就是拓扑排序的顺序。

bool dfs (int x) {int Max = 100;fl[x] = -1;for (int i = 0; i < G[x].size(); i ++) {if (fl[G[x][i]] == -1) {return 0;} else if (fl[G[x][i]] == 0 && !dfs (G[x][i])) {return 0;} else {Max = max (Max, topo[G[x][i]] + 1);}}fl[x] = 1;topo[x] = Max;return 1;
}bool toposort () {for (int i = 1; i <= n; i ++) {if (!fl[i]) {if (!dfs (i)) {return 0;}}}return 1;
}

注意：代码中fl[i]数组用来记录状态。

• 若$f{l}_i=0$，表示$i$点没有被访问过;
• 若$f{l}_i=1$，表示$i$点已经被访问过;
• 若$f{l}_i=0$，表示$i$点正在访问。

拓扑排序的作用：

1. 解决$AOV$网的排序问题;
2. 判断一个有向图是否为$AOV$网，即判断一个有向图是否有环。

三、关键路径

(1) $AOV$网和$AOE$网

$AOV$网：$DAG$，有向无环图。

$AOE$网：带权有向图。

(2) 在关键路径中的术语

1. 源点(起始点)：入度为$0$的点。
2. 汇点(终点)：出度为$0$的点。
3. 路径长度：整条路径上的权值之和。
4. 关键路径：在$AOE$网中，从源点到汇点具有最大长度的路径。

Day 25：新知——欧拉回路

学习笔记

一、定义

1. 欧拉回路：通过图中每条边，且每条边只通过一次，并且经过每个顶点的回路。
2. 欧拉通路：通过图中每条边，且每条边只通过一次，并且经过每个顶点的通路。
3. 有向图的基图：忽略所有有向边的方向，得到的无向图就是这个有向图的基图。

解释一下：回路是指从起点出发，经过所有边再回到起点的路径;通路是指从起点出发，经过所有边后到达终点(起点$\ne$终点)的路径。

具有欧拉回路的图称为欧拉图，具有欧拉通路的图称为半欧拉图。

二、欧拉回路&欧拉通路的性质

(1) 无向图

无向图$G$为连通图，且$G$中有且仅有$2$个顶点的度数为奇数，则图$G$为欧拉通路，其中，两个度数为奇数的顶点必定为起点和终点。

无向图$G$为连通图，且$G$中任意顶点的的度数均为偶数，则图$G$为欧拉回路。

(2) 有向图

有向图$D$的基图为连通图，且满足$D$中有且仅有$2$个点的入度不等于出度，而在这两个点中，一个出度比入度多$1$，另一个入度比出度大$1$，则图$D$为欧拉通路，其中，出度比入度大$1$的点为起点，入度比出度大$1$的点为终点。

有向图$D$的基图为连通图，且$D$中任意顶点的出度均等于入度，则图$D$为欧拉回路。

三、解法

(1) DFS

#include <cstdio>
#include <algorithm>
#include <cstring>
#define inf 0x3f3f3f3f
using namespace std;const int MAXN = 2000 + 5;
int G[MAXN][MAXN], d[MAXN], ans[MAXN], n, x, y, t;
int Max = -inf, Min = inf;void dfs (int x) {for (int i = Min; i <= Max; i ++) {if (G[x][i]) {G[x][i] --; G[i][x] --;dfs (i);}}ans[++ t] = x;
}int main () {scanf ("%d", &n);for (int i = 1; i <= n; i ++) {scanf ("%d %d", &x, &y);G[x][y] ++, G[y][x] ++;Max = max (Max, max (x, y)); Min = min (Min, min (x, y));d[x] ++, d[y] ++;}bool flag = 0;for (int i = Min; i <= Max; i ++) {if (d[i] % 2 == 1) {flag = 1;dfs (i);break;}}if (!flag) dfs (Min);for (int i = t; i >= 1; i --) {printf ("%d ", ans[i]);}return 0;
}

(2) Fleury算法

算法原理：

设图$G$是一个无向欧拉图。

1. 任意在图$G$中取一顶点$V_0$，令路径$P_0=V_0$;
2. 假设沿着路径$P_i=V_0{E}_1{V}_1{E}_2{V}_2{E}_3{V}_3...E_i{V}_i$走到点$V_i$，按照下面方法从 E ( G ) − { E 1 , E 2 , E 3 , . . . , E i } E(G)-\{E_1,E_2,E_3,...,E_i\} E(G)−{E1​,E2​,E3​,...,Ei​}中选择一边作为$E_{i+1}$：

• $E_{i+1}$与$V_i$相连;
• $E_{i+1}$不应该是 E ( G ) − { E 1 , E 2 , E 3 , . . . , E i } E(G)-\{E_1,E_2,E_3,...,E_i\} E(G)−{E1​,E2​,E3​,...,Ei​}中的桥。

3. 当(2)不能再进行的这时候，得到的回路$P_m=V_0{E}_1{V}_1{E}_2{V}_2{E}_3{V}_3...V_m(V_m=V_0)$为$G$中的一条欧拉回路。

注：无向图$G(V,E)$为连通图，若边集$E1\in E$，再图$G$中删除$E1$后得到的子图不连通，且删除$E1$的任意真子集后得到的子图为连通图，则称$E1$是$G$的一个割边集。若一条边构成了一个割边集，则称该边为割边(桥)。

说点人话吧…

如下图，若删除了一条边，整个图会分裂成两个独立的子图，则称这条边为桥。(如红边)

int G[MAXN][MAXN];
stack <int> st;void dfs (int x) {st.push(x);for (int i = 1; i <= n; i ++) {if (G[x][i] > 0) {G[x][i] --, G[i][x] --;dfs (i);break;}}
}void fleury (int x) {st.push(x);while (st.size()) {bool flag = 0;int pos = st.top();for (int i = 1; i <= n; i ++) {if (G[pos][i] > 0) {fl = 1;break;}}if (!flag) {printf ("%d ", pos);st.pop();} else {st.pop();dfs (pos);}}
}int main () {scanf ("%d %d", &n, &m);for (int i = 1; i <= m; i ++) {scanf ("%d %d", &x, &y);G[x][y] ++, G[y][x] ++;d[x] ++, d[y] ++;}int num = 0, start = 1;for (int i = 1; i <= n; i ++) {if (d[i] % 2 == 1) {start = i, num ++;}}if (num == 0 || num == 2) {fleury (start);} else {puts ("No Euler Path");}
}