高性能数值计算编程小技巧(带实例，持续更新.......)

1、乘法比除法运算速度更快，一般情况下，尽量用乘法代替除法

  $a=0.5\ast b$与$a=b/2.0$分别计算1000000次。在笔者的程序运行环境下，前者运行时间1.62ms，后者运行时间3.85ms(不同平台结果不一样)。乘法计算效率大概是除法的2.3倍！

#include <time.h>
#include <stdio.h>
#include <math.h>
#define TEST_COUNT 100
#define CALCULATE_COUNT 1000000double calculate_mean_runtime(double timeArray[]);
double calculate_std_runtime(double timeArray[], double meanRuntime);double calculate_mean_runtime(double timeArray[])
{long n;double sum = 0.0;for (n = 0; n < TEST_COUNT; n++){sum += timeArray[n];}return sum / TEST_COUNT;
}double calculate_std_runtime(double timeArray[], double meanRuntime)
{long n;double sum = 0.0;for (n = 0; n < TEST_COUNT; n++){sum += (timeArray[n] - meanRuntime) * (timeArray[n] - meanRuntime);}return sqrt(sum / (TEST_COUNT - 1));
}void main(void)
{long i, n, startTime, finishTime;double meanRuntime, stdRuntime, timeArray[TEST_COUNT];double a, b = 1.0;for (n = 0; n < TEST_COUNT; n++){startTime = clock();for (i = 0; i < CALCULATE_COUNT; i++){//a = 0.5 * b;a = b / 2.0;}finishTime = clock();timeArray[n] = (double)(finishTime - startTime);}meanRuntime = calculate_mean_runtime(timeArray);stdRuntime = calculate_std_runtime(timeArray, meanRuntime);printf("The mean run time is:%f ms!\n", meanRuntime);printf("The std run time is:%f ms!\n", stdRuntime);
}

2、两相近的数相减，会导致计算精度丢失，应想办法将减法运算转化为其他运算

  在一定条件下，利用恒等变换，可以将减法运算转化为其他运算，从而提高计算精度。以下函数的取值均在定义域内。
  1).当$x\to 0$时，作变换：
$$1-cosx=2si{n}^2(\frac{x}{2})\text{\hspace{1em}(1)}$$
  2).当$x_1$与$x_2$很接近时，作变换：
$$lo{g}_a{x}_1-lo{g}_a{x}_2=lo{g}_a\frac{x_1}{x_2}\text{\hspace{1em}(2)}$$
  3).当$x$较大时，作变换：
$$\sqrt{x+1}-\sqrt{x}=\frac{1}{\sqrt{x+1}+\sqrt{x}}\text{\hspace{1em}(3.1)}$$
$$lo{g}_a(x-\sqrt{x^2-1})=-lo{g}_a(x+\sqrt{x^2-1})\text{\hspace{1em}(3.2)}$$
$$arctan(x+1)-arctan(x)=arctan(\frac{1}{x^2+x+1})\text{\hspace{1em}(3.3)}$$
  令$arctan(x+1)=A,arctan(x)=B$，$tan(A-B)=\frac{tan(A)-tan(B)}{1+tan(A)tan(B)}=\frac{x+1-x}{1+(x+1)x}=\frac{1}{x^2+x+1}$，则$A-B=arctan(\frac{1}{x^2+x+1})$，上式得证。
  4).当$b^2>>4ac$时，对于一元二次方程求根公式$x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$，作变换(详见博文:一元二次方程高精度实数根(C语言))：
$$x_1=\frac{-2c}{b+\sqrt{b^2-4ac}}(b>0)\text{\hspace{1em}(4.1)}$$
$$x_2=\frac{-2c}{b-\sqrt{b^2-4ac}}(b<0)\text{\hspace{1em}(4.2)}$$
  5).当$f(x)\approx f(x^{\ast })$时，利用泰勒展开，作变换：
$$f(x)-f(x^{\ast })=f^{\prime }(x^{\ast })(x-x^{\ast })+\frac{f^{\prime \prime }(x^{\ast })}{2}(x-x^{\ast }{)}^2+\cdots \text{\hspace{1em}(5)}$$

#include <stdio.h>
#include <math.h>void main(void)
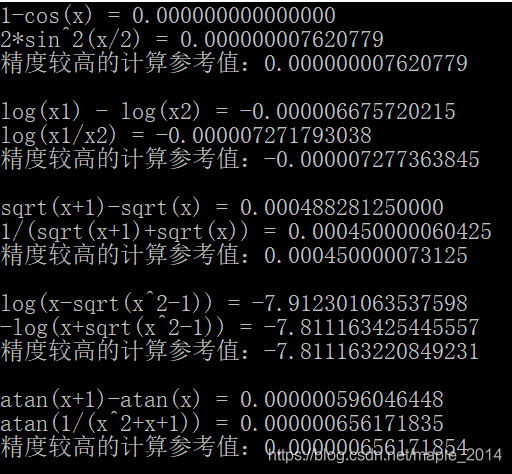
{float x, x1, x2;double xx, xx1, xx2;//(1)x = 1.234567e-4f;xx = (double)x;printf("1-cos(x) = %.15f\n", 1.0 - cosf(x));printf("2*sin^2(x/2) = %.15f\n", 2.0 * sinf(x / 2.0) * sinf(x / 2.0));printf("精度较高的计算参考值：%.15f\n\n", 2.0 * sin(xx / 2.0) * sin(xx / 2.0));//(2)x1 = 123456.0f;x2 = 123456.9f;xx1 = (double)x1;xx2 = (double)x2;printf("log(x1) - log(x2) = %.15f\n", logf(x1) - logf(x2));printf("log(x1/x2) = %.15f\n", logf(x1 / x2));printf("精度较高的计算参考值：%.15f\n\n", log(xx1 / xx2));//(3.1)x = 1234567.0f;xx = (double)x;printf("sqrt(x+1)-sqrt(x) = %.15f\n", sqrtf(x + 1) - sqrtf(x));printf("1/(sqrt(x+1)+sqrt(x)) = %.15f\n", 1.0 / (sqrtf(x + 1) + sqrtf(x)));printf("精度较高的计算参考值：%.15f\n\n", 1.0 / (sqrt(xx + 1) + sqrt(xx)));//(3.2)x = 1234.0f;xx = (double)x;printf("log(x-sqrt(x^2-1)) = %.15f\n", logf(x - sqrtf(x * x - 1.0)));printf("-log(x+sqrt(x^2-1)) = %.15f\n", -logf(x + sqrtf(x * x - 1.0)));printf("精度较高的计算参考值：%.15f\n\n", -log(xx + sqrt(xx * xx - 1.0)));//(3.3)printf("atan(x+1)-atan(x) = %.15f\n", atanf(x + 1) - atanf(x));printf("atan(1/(x^2+x+1)) = %.15f\n", atanf(1.0 / (x * x + x + 1.0)));printf("精度较高的计算参考值：%.15f\n", atan(1.0 / (xx * xx + xx + 1.0)));
}

3、多项式求值时，采用霍纳方法(或秦九韶方法)的递推公式，减小计算量，提高计算精度及可靠性

  具体参见博文:多项式求值(Evaluation of a Polynomial)

4、将不变条件的计算移到循环体外

  将循环中与循环无关，不是每次循环都要做的操作，移到循环外部执行。
  示例一：

for (int i = 0; i < 10; i++ )
{sum += i;back_sum = sum;
}

  对于此for循环来说语句“back_Sum = sum;” 没必要每次都执行，只需要执行一次即可，因此可以改为：

for (int i = 0; i < 10; i++ )
{sum += i;
}
back_sum = sum;

  示例二：

for (_UL i = 0; i < func_calc_max(); i++)
{//process;
}

  函数func_calc_max()没必要每次都执行，只需要执行一次即可，因此可以改为：

_UL max = func_calc_max();
for (_UL i = 0; i < max; i++)
{//process;
}

5、对于多维大数组，避免来回跳跃式访问数组成员

  多维数组在内存中是从最后一维开始逐维展开连续存储的。下面这个对二维数组访问是以SIZE_B为步长跳跃访问，到尾部后再从头（第二个成员）开始，依此类推。局部性比较差，当步长较大时，可能造成cache不命中，反复从内存加载数据到cache。应该把i和j交换。

for (int i = 0; i < SIZE_B; i++)
{for (int j = 0; j < SIZE_A; j++){sum += x[j][i];}
}

  上面这段代码，在 SIZE_B 数值较大时，效率可能会比下面的代码低:

for (int i = 0; i < SIZE_B; i++)
{for (int j = 0; j < SIZE_A; j++){sum += x[i][j];}
}

6、创建资源库，以减少分配对象的开销

  例如，使用线程池机制，避免线程频繁创建、销毁的系统调用；使用内存池，对于频繁申请、释放的小块内存，一次性申请一个大块的内存，当系统申请内存时，从内存池获取小块内存，使用完毕再释放到内存池中，避免内存申请释放的频繁系统调用。

7、将多次被调用的 “小函数”改为inline函数或者宏实现

  如果编译器支持inline，可以采用inline函数。否则可以采用宏。在做这种优化的时候一定要注意下面inline函数的优点：其一编译时不用展开，代码SIZE小。其二可以加断点，易于定位问题，例如对于引用计数加减的时候。其三函数编译时，编译器会做语法检查。

8、内存不紧张情况下，可考虑空间换时间的策略，提高计算效率

  以下程序效率低下：

for (i = 0; i < 1000; i++)
{x[i] = a[i] * sin(theta[i]) + b[i] * cos(theta[i]);y[i] = b[i] * sin(theta[i]) + a[i] * sin(theta[i]);
}

  可以改为：

for (i = 0; i < 1000; i++)
{sinTheta = sin(theta[i]);cosTheta = cos(theta[i]);x[i] = a[i] * sinTheta + b[i] * cosTheta;y[i] = b[i] * sinTheta + a[i] * cosTheta;
}

参考文献

华为C语言编程规范 2011年5月9日发布
《数值分析》李庆扬，王能超，易大义编