本博客的代码的思想和图片参考:好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》
陈越姥姥,我向您说明的是,在您这个算法中,只能实现一个链表的从第一个元素到K个元素的反转,但是不能实现每K个元素的反转
Ptr Reverse( Ptr head, int K ) { cnt = 1;new = head->next;old = new->next;while ( cnt < K ) {tmp = old->next;old->next = new;new = old; old = tmp;cnt++;}head->next->next = old;return new; }
这是根据您的视频我画的演示的图,当K=3时:
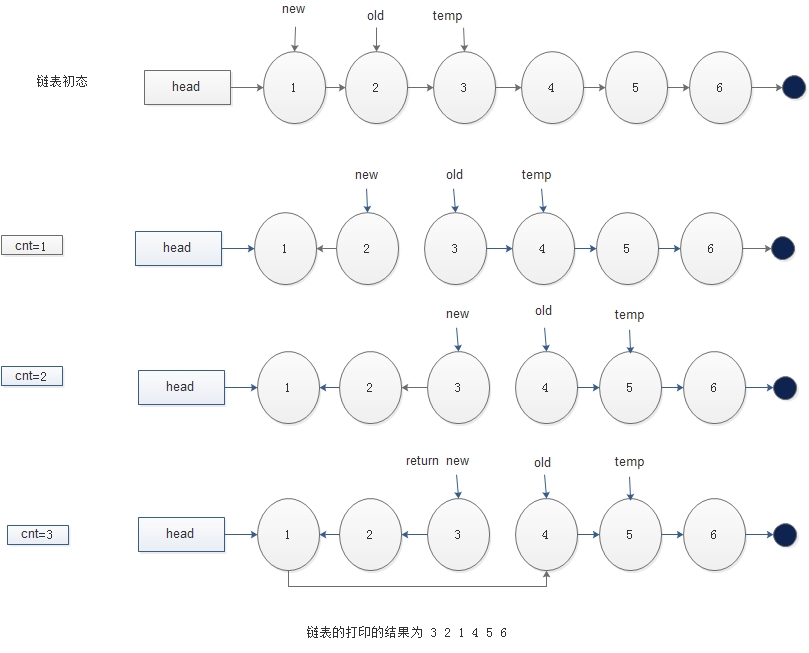
我的意思是:那个测验题要求我们每K个元素进行反转,

也就是 当K=3时,链表的打印应该为结果为 3 2 1 6 5 4,链表的结构按照您的算法思路应该如下图所示
但是您的算法却没有把这个题目要求实现。这就是我昨晚很迷惑的地方
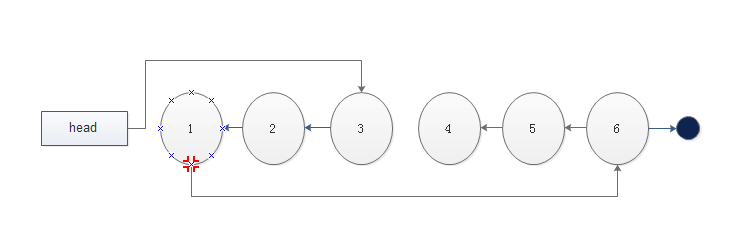
但是我今天想了一下,您应该是只教了我们如何去把一个链表的前N个元素反转,但是关于这道题目,还是由我们自己根据您提供的思路来写题目要求的算法。
很抱歉,昨天晚上打扰到陈越姥姥了。
但是我想了一晚上,也没想出来(大哭),陈越姥姥能不能给点思路呀。
也就是





