本文主要是介绍用位运算实现加减乘除法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们知道计算机只认识0和1,而计算机在计算加减乘除的是也不是我们理解的直接预算,而是通过逻辑运算来实现的,也就是与、非、或、异或,下面就通过这些逻辑运算符来实现加减乘除法
加法:比如1+1用二进制表示就是00000001+00000001,那么在不允许直接使用加号的时候,我们就可以用异或来实现加法,异或实际上就可以理解为不进位的加法,00000001异或00000001就等于00000000,丢掉了一个进位,而进位信息,可以通过与运算来保留,与运算的时候,必须是两个1,结果才会是1,也就是说对应的位上一定是两个1,相加的时候一定会产生进位,那么加法的实现就是不进位相加的结果+进位信息,也就是异或运算的结果加上与运算产生的进位,进位就是与运算之后乘以2,也就是左移一位,直到进位为0为止:
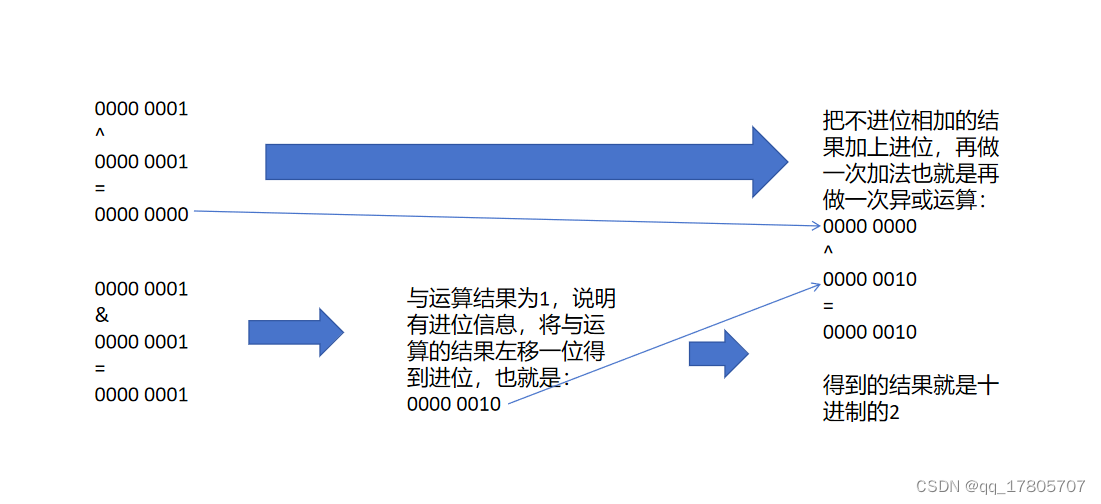
代码实现:
public static int add(int a, int b) {while (b != 0) {int carry = a & b; // 进位a = a ^ b; // 不考虑进位的加法b = carry << 1; // 将进位左移一位}return a;}减法:有两种方式,一种是跟加法一样,通过借位
public static int subtract(int a, int b) {while (b != 0) {int borrow = (~a) & b;a = a ^ b;b = borrow << 1;}return a;}-
while (b != 0):这是一个循环,只要b不等于0,就继续执行循环体。这是因为在二进制中,0代表没有借位,所以当b变为0时,表示减法已经完成。 -
int borrow = (~a) & b;:这行代码计算了借位。~a对a取反,然后与b进行与运算,结果为借位。如果a的某一位是0,b的相应位是1,那么需要从更高位借1,这就产生了借位。 -
a = a ^ b;:这行代码实现了无借位的减法。^是异或运算符,对于每一位,如果a和b的相应位都是1或都是0,那么结果就是0(1-1=0,0-0=0);如果a的位是1,b的位是0,那么结果就是1(1-0=1)。这就完成了无借位的减法。 -
b = borrow << 1;:这行代码将借位左移一位。因为借位实际上是从更高位借来的,所以需要左移一位。 -
return a;:最后返回a,这就是减法的结果
第二种就是直接使用加法来实现减法:比如2-1实际上就是2加上-1,-1实际上就是1取反再加1:
public static int subtractV2(int a, int b) {return add(a, add(~b, 1));}乘法:乘法实际上还是加法的实现,比如我们知道5*3实际上就是5个3相加或者3个5相加,我们用二进制加法来表示5*3:

public static int muti(int a, int b) {int res = 0;while (b != 0) {if ((b & 1) == 1) {//说明b无符号右移之后最后一位是1,这个时候就需要把a加上去,否则继续移动res = add(a, res);}b = b >>> 1;a = a << 1;}return res;}除法:除法是乘法的反向推导,比较绕,比如15/5=3,意思就是5*2+5*1=15,其中2就是2的一次方,1就是2的0次方,也就是说一个数a除以b,那么a一定可以表示为:b*2的0次方+b*2的1次方+....,我们说乘法实际上是加法实现的,那么除法其实就是减法的实现过程,比如15/5,也就是从15中不断地减去5,直到不够减或者为0为止,也就是:15-5*2-5*1=0,其中2就是2的一次方,1就是2的0次方,那么15/5实际上就是2的0次方加上2的一次方
/*** 转换成绝对值* 5取反是-6* -5取反是4** @param n* @return*/public static int negNum(int n) {return add(~n, 1);}/*** 除法其实就是乘法的反向推导* 比如15/5=3* 15=5*3 ===》0101*2+0101 ==》01010+00101 ==》01111* 15=5*3 ===》5*2+5*1 ==》01010+00101 ==》01111* 5左移动一位10 两位是20* res*2*1+res*1*/public static int div(int a, int b) {int x = Math.abs(a);//先转换成绝对值计算,最后判断结果要不要加上-号,绝对值可以通过上面的negNum来实现int y = Math.abs(b);//先转换成绝对值计算,最后判断结果要不要加上-号,绝对值可以通过上面的negNum来实现int res = 0;for (int i = 30; i >= 0; i = subtractV2(i, 1)) {if ((x >> i) >= y) {//res = res | (1 << i);x = subtractV2(x, y << i);}}return (a > 0 && b > 0) ? res : muti(res, -1);}这篇关于用位运算实现加减乘除法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







