4229. 【五校联考4day1】学习神技

Description

王仙女打开了《葵花宝典》，第一页上赫然写道：欲练此功，必先学习上古神技：等比数列求和！
王仙女心想：等比数列是什么**东西？难道我的修仙之路要止步于此了吗？
还好，天无绝人之路，在宝典的第二页上，写着密密麻麻的等比数列的介绍：
等比数列为这样一个数列，它的首项为a_1,第i项为a_1*q^(i-1)，其中q为此等比数列的公比。等比数列前n项的求和公式为：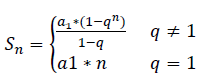

聪慧过人的仙女一下子就学会了等比数列的求和，可是他发现宝典上还有M道测试题，可是这M道的n都非常的大，仙女一时间算不出来，只好打通时空隧道向未来的你求助。有现代化计算机帮助的你一定能很快的求出这M个答案的对吧？

Input

第一行一个正整数M，为询问组数
接下来M行，每行三个正整数a_1,q,n，含义如题。

Output

共M行，为M个询问的答案。答案对〖10〗^9+7取模。

Sample Input

1
2 3 3

Sample Output

26

Data Constraint

对于30%的数据，M≤1000，对于每一个询问，n≤1000
对于100%的数据，M≤〖10〗^5，a_1,q≤〖10〗^9，n≤〖10〗^18

Solution 

对于q=1时，直接a%MOD*p%MOD。】

对于q<>1时，求出q-1在%MOD的意义下的逆元，然后直接乘起来就好了。

Code

#include<cstdio> 
#include<cstring>
#include<algorithm>
#define ll long long
#define M 1000000007
using namespace std;
ll a,q,q2,n,T,ans;
ll ksm(ll x,ll k){if(k==0) return 1;if(k==1) return x%M;ll t=ksm(x,k/2)%M;if(k&1) return ((t*t)%M*x)%M;return t*t%M;
}
ll read(){ll w=1,x=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return w*x;
}
int main(){T=read();while(T--){a=read(),q=read(),n=read();if(q==1){printf("%lld\n",(n%M)*(a%M)%M);}else{q2=ksm(q-1,M-2);ans=((q2*a)%M*(ksm(q,n)-1+M)%M);printf("%lld\n",ans);}}return 0;
}

作者：zsjzliziyang 
QQ:1634151125 
转载及修改请注明 
本文地址:https://blog.csdn.net/zsjzliziyang/article/details/86584562