本文主要是介绍西电计科院大学物理二期中复习笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大学物理二期中复习笔记
博主是21级计科院的,大学物理二97分,这是期中复习期间整理的笔记,基本全部涵盖期中考试重点范围,有需要的学弟学妹可以作为参考
详情请参考我的博客文章
第一章 静电场

第一讲 库仑定律
库仑定理——(真空静止点电荷)
F = 1 4 π ε 0 q 1 q 2 r 2 r 0 (1) F = \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r^2}\boldsymbol{r}^0\tag 1 F=4πε01r2q1q2r0(1)
其中真空介电常数 ε 0 ≈ 8.85 × 1 0 − 12 C 2 N − 1 m − 2 \varepsilon_0 \approx 8.85\times10^{-12} C^2N^{-1}m^{-2} ε0≈8.85×10−12C2N−1m−2,令 k = 1 4 π ε 0 k=\frac{1}{4\pi\varepsilon_0} k=4πε01 则 k ≈ 9 × 1 0 9 N m 2 / C 2 k\approx 9\times 10^9Nm^2/C^2 k≈9×109Nm2/C2,矢量 r 0 \boldsymbol{r}^0 r0 由施力电荷指向受力电荷
第二讲 电场强度 E E E
2.1 电场强度
E = F q 0 = 1 4 π ε 0 q r 2 r 0 (2) E = \frac{F}{q_0}=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}\boldsymbol{r}^0\tag 2 E=q0F=4πε01r2qr0(2)
2.2 均匀带电细圆环
圆环轴线上一点 P P P的电场强度:
E = 1 4 π ε 0 q x ( R 2 + x 2 ) 3 2 (3) E = \frac{1}{4\pi\varepsilon_0}\frac{qx}{(R^2+x^2)^\frac{3}{2}}\tag 3 E=4πε01(R2+x2)23qx(3)
其中, x x x表示 P P P点到圆环中心 O O O的距离, R R R表示圆环半径, q q q表示圆环带电量;
2.3 有限长直线段
直线外一点 P P P电场强度:
E x = λ 4 π ε 0 a ( c o s θ 1 − c o s θ 2 ) E y = λ 4 π ε 0 a ( s i n θ 2 − s i n θ 1 ) (4) E_x=\frac{\lambda}{4\pi\varepsilon_0 a}(cos\theta_1-cos\theta_2)\\ E_y=\frac{\lambda}{4\pi\varepsilon_0 a}(sin\theta_2-sin\theta_1)\tag 4 Ex=4πε0aλ(cosθ1−cosθ2)Ey=4πε0aλ(sinθ2−sinθ1)(4)
注:在建立坐标系的情况下,上式均带有方向,其中沿 y y y 轴正向: θ 1 → θ 2 \theta_1\rightarrow \theta_2 θ1→θ2, θ \theta θ 为与 y y y 轴正向夹角;
其中, a a a表示 P P P点到直线的垂直距离;
2.4 均匀带电无限长直线
由 2.4 2.4 2.4 推得:令 θ 1 = 0 , θ 2 = π \theta_1=0,\theta_2=\pi θ1=0,θ2=π
E x = λ 2 π ε 0 a , E y = 0 (5) E_x = \frac{\lambda}{2\pi\varepsilon_0 a}, E_y = 0\tag 5 Ex=2πε0aλ,Ey=0(5)
2.5 均匀带电无限大平面
E = σ 2 ε 0 (6) E=\frac{\sigma}{2\varepsilon_0} \tag 6 E=2ε0σ(6)
2.6 无限大均匀带异号电荷平板间
E = σ ε 0 (7) E=\frac{\sigma}{\varepsilon_0}\tag 7 E=ε0σ(7)
其中, σ \sigma σ表示每个平板的电荷面密度;
2.7 电偶极子
电偶极矩: p = q l \boldsymbol{p}=q\boldsymbol{l} p=ql
中垂线上一点 P P P场强:
E = − p 4 π ε 0 y 3 ( y ≫ l ) (8) E = -\frac{\boldsymbol{p}}{4\pi\varepsilon_0y^3} (y\gg l)\tag 8 E=−4πε0y3p(y≫l)(8)
共线上一点 P P P场强:
E = 2 p 4 π ε 0 x 3 ( x ≫ l ) (9) E=\frac{2\boldsymbol{p}}{4\pi\varepsilon_0x^3}(x\gg l)\tag 9 E=4πε0x32p(x≫l)(9)
其中 l \boldsymbol{l} l方向由负电荷指向正电荷;
2.8 力偶矩
电偶极子在匀强电场中得力偶矩:
F + = q E , F − = − q E M = F + ⋅ 1 2 l s i n θ + F − ⋅ 1 2 l s i n θ = q l E s i n θ ⇒ M = q l × E = p × E (10) \boldsymbol{F}_+=q\boldsymbol{E},\boldsymbol{F}_-=-q\boldsymbol{E}\\ M = F_+\cdot\frac{1}{2}lsin\theta+F_-\cdot\frac{1}{2}lsin\theta=qlEsin\theta\\ \Rightarrow\boldsymbol{M}=q\boldsymbol{l}\times\boldsymbol{E}=\boldsymbol{p}\times\boldsymbol{E}\tag{10} F+=qE,F−=−qEM=F+⋅21lsinθ+F−⋅21lsinθ=qlEsinθ⇒M=ql×E=p×E(10)
注:电偶极子在电场的作用下总要使 p \boldsymbol{p} p 转向 E \boldsymbol{E} E 的方向;
第三讲 电通量 ★ \bigstar ★高斯定理
3.1 电通量
Φ e = ∮ S E ⋅ d S (11) \Phi_e=\oint_S\boldsymbol{E}\cdot d\boldsymbol{S}\tag{11} Φe=∮SE⋅dS(11)
3.2 高斯定理
选定高斯面后,电通量:
Φ e = ∮ S E ⋅ d S = 1 ε 0 ∑ ( 内 ) q i (12) \Phi_e=\oint_S\boldsymbol{E}\cdot d\boldsymbol{S}=\frac{1}{\varepsilon_0}\sum_{(内)}q_i\tag{12} Φe=∮SE⋅dS=ε01(内)∑qi(12)
3.3 轴对称性电场
无限长均匀带电直线外一点 P P P场强:
Φ e = E ∮ 侧 d S = 2 π r E l = 1 ε 0 λ l ⇒ E = λ 2 π ε 0 r (13) \Phi_e=\boldsymbol{E}\oint_侧d\boldsymbol{S}=2\pi rEl=\frac{1}{\varepsilon_0}\lambda l\\ \Rightarrow E = \frac{\lambda}{2\pi\varepsilon_0r}\tag{13} Φe=E∮侧dS=2πrEl=ε01λl⇒E=2πε0rλ(13)
其中, r r r表示 P P P距离导线垂直距离;
3.4 球面对称性电场
均匀带电球面电场分布:
Φ e = E ∮ S S = E ⋅ 4 π r 2 = ∑ ( 内 ) q i = q ⇒ E = { 1 4 π ε 0 q r 2 r 0 ( r > R ) 0 ( r < R ) (14) \Phi_e=\boldsymbol{E}\oint_S\boldsymbol{S}=E\cdot 4\pi r^2=\sum_{(内)}q_i=q\\ \Rightarrow E=\left\{\begin{array}{lcc} \frac{1}{4\pi \varepsilon_0}\frac{q}{r^2}\boldsymbol{r}^0&(r>R) \\ 0&(r<R)\tag{14}\end{array}\right. Φe=E∮SS=E⋅4πr2=(内)∑qi=q⇒E={4πε01r2qr00(r>R)(r<R)(14)
3.5 无限大均匀带电平面
选定圆柱面作为高斯面:
Φ e = ∮ 左端面 E ⋅ d S + ∮ 右端面 E ⋅ d S = 2 E S = 1 ε 0 σ S ⇒ E = σ 2 ε 0 (15) \Phi_e=\oint_{左端面}\boldsymbol{E}\cdot d\boldsymbol{S}+\oint_{右端面}\boldsymbol{E}\cdot d\boldsymbol{S}=2ES=\frac{1}{\varepsilon_0}\sigma S\\ \Rightarrow E=\frac{\sigma}{2\varepsilon_0}\tag{15} Φe=∮左端面E⋅dS+∮右端面E⋅dS=2ES=ε01σS⇒E=2ε0σ(15)
3.6 均匀带电圆盘
E = σ 2 ε 0 ( 1 − x R 2 + x 2 ) (16) E = \frac{\sigma}{2\varepsilon_0}(1-\frac{x}{\sqrt{R^2+x^2}})\tag{16} E=2ε0σ(1−R2+x2x)(16)
3.7 均匀带电球体
E = { Q 4 π ε 0 r 2 r 0 ( r > R ) ρ 3 ε 0 r ( r < R ) \boldsymbol{E}=\left\{\begin{array}{c}\frac{Q}{4\pi\varepsilon_0r^2}\boldsymbol{r_0}&(r>R)\\\frac{\rho}{3\varepsilon_0}\boldsymbol{r} & (r<R)\end{array}\right. E={4πε0r2Qr03ε0ρr(r>R)(r<R)
第四讲 静电场的环路定理 电势能
4.1 电场强度环流
∮ E ⋅ d l = 0 (17) \oint\boldsymbol{E}\cdot d\boldsymbol{l}=0\tag{17} ∮E⋅dl=0(17)
环路定理表明静电场是无旋有源场;
4.2 电势能
选定电势能零参考点,则点 A A A处的电势能:
w a = A a ′ 0 ′ = ∫ a ′ 0 ′ q 0 E ⋅ d l (18) w_a=A_{a'0'}=\int_a^{'0'}q_0\boldsymbol{E}\cdot d\boldsymbol{l}\tag{18} wa=Aa′0′=∫a′0′q0E⋅dl(18)
注:电势能是标量,相对于电势能零参考点有负值;
第五讲 电势 电势差
5.1 电势与电势差
A A A点电势:
u a = W a q 0 = ∫ a ′ 0 ′ E ⋅ d l (19) u_a=\frac{W_a}{q_0}=\int_a^{'0'}\boldsymbol{E}\cdot d\boldsymbol{l}\tag{19} ua=q0Wa=∫a′0′E⋅dl(19)
注:电势为标量;
U a b = u a − u b = ∫ a b E ⋅ d l (20) U_{ab}=u_a-u_b=\int_a^b\boldsymbol{E}\cdot d\boldsymbol{l}\tag{20} Uab=ua−ub=∫abE⋅dl(20)
电荷 q q q a → b a\rightarrow b a→b时,静电力做功:
A a b = q ( u a − u b ) (21) A_{ab}=q(u_a-u_b)\tag{21} Aab=q(ua−ub)(21)
5.2 电偶极子电势能
在电场 E \boldsymbol{E} E 中:
W = − p ⋅ E (22) W=-\boldsymbol{p}\cdot\boldsymbol{E}\tag{22} W=−p⋅E(22)
当 E \boldsymbol{E} E为非均匀电场时,上式应改为积分形式;
在电场中做功:
W θ 1 θ 2 = { − p ⋅ E ( θ 1 ) − ( − p ⋅ E ( θ 2 ) ) ∫ θ 1 θ 2 − p × E d θ W_{\theta_1\theta_2}=\left\{\begin{array}{ll}-\boldsymbol{p}\cdot\boldsymbol{E}(\theta_1)-(-\boldsymbol{p}\cdot\boldsymbol{E}(\theta_2))\\ \int_{\theta_1}^{\theta_2}-\boldsymbol{p}\times\boldsymbol{E}d\theta\end{array}\right. Wθ1θ2={−p⋅E(θ1)−(−p⋅E(θ2))∫θ1θ2−p×Edθ
5.3 电势叠加原理
对于点电荷选取无穷远处作为零电势点:
u a = ∫ a ∞ E ⋅ d l = 1 4 π ε 0 q r W a = 1 4 π ε 0 q 2 r (23) u_a=\int_a^{\infty}\boldsymbol{E}\cdot d\boldsymbol{l}=\frac{1}{4\pi\varepsilon_0}\frac{q}{r}\\ W_a = \frac{1}{4\pi\varepsilon_0}\frac{q^2}{r}\tag{23} ua=∫a∞E⋅dl=4πε01rqWa=4πε01rq2(23)
叠加原理——标量叠加
u a = ∑ u i ⇒ u a = ∫ Q 1 4 π ε 0 d q r ( 积分形式 ) (24) u_a=\sum u_i\\ \Rightarrow u_a=\int_Q\frac{1}{4\pi\varepsilon_0}\frac{dq}{r}(积分形式)\tag{24} ua=∑ui⇒ua=∫Q4πε01rdq(积分形式)(24)
5.4 电荷分布求电势
积分形式:
u a = ∫ Q 1 4 π ε 0 d q r (25) u_a=\int_Q\frac{1}{4\pi\varepsilon_0}\frac{dq}{r}\tag{25} ua=∫Q4πε01rdq(25)
电偶极子外任一点 C C C的电势:
U C = 1 4 π ε 0 q r + − 1 4 π ε 0 q r − = q 4 π ε 0 r − − r + r − r + r ≫ l ⇒ r + r − ≈ r 2 , r − − r + ≈ l c o s θ ⇒ u C = 1 4 π ε 0 p ⋅ r r 3 (26) U_C = \frac{1}{4\pi\varepsilon_0}\frac{q}{r_+}-\frac{1}{4\pi\varepsilon_0}\frac{q}{r_-}=\frac{q}{4\pi\varepsilon_0}\frac{r_--r_+}{r_-r_+}\\ r\gg l\Rightarrow r_+r_-\approx r^2,r_--r_+\approx lcos\theta\\ \Rightarrow u_C = \frac{1}{4\pi\varepsilon_0}\frac{\boldsymbol{p}\cdot\boldsymbol{r}}{r^3}\tag{26} UC=4πε01r+q−4πε01r−q=4πε0qr−r+r−−r+r≫l⇒r+r−≈r2,r−−r+≈lcosθ⇒uC=4πε01r3p⋅r(26)
5.5 电场强度求电势
场强与电势关系:
u a = ∫ a ∞ E ⋅ d l (27) u_a=\int_a^{\infty}\boldsymbol{E}\cdot d\boldsymbol{l}\tag{27} ua=∫a∞E⋅dl(27)
带电体电荷分布具有对称性时,利用高斯定理求出场强分布进而求电势;
【无限长均匀带电圆柱面】
由高斯定理求得电场分布:
E = { 0 r < R λ 2 π ε 0 r r > R (28) E = \left\{ \begin{array}{c}0 & r<R \\ \frac{\lambda}{2\pi\varepsilon_0r} & r>R\end{array}\right.\tag{28} E={02πε0rλr<Rr>R(28)
一般而言,当电荷分布延伸到无穷远时,是不能选取无穷远处为电势零参考点的;
u P = ∫ P P 0 E ⋅ d l = ∫ P P ′ E ⋅ d l + ∫ P ′ P 0 E ⋅ d l = 0 + ∫ r r 0 λ 2 π ε 0 r d r = − λ 2 π ε 0 ln r + λ 2 π ε 0 ln r 0 = − λ 2 π ε 0 ln r + C ( r > R ) (29) u_P=\int_P^{P_0}\boldsymbol{E}\cdot d\boldsymbol{l}=\int_P^{P'}\boldsymbol{E}\cdot d\boldsymbol{l}+\int_{P'}^{P_0}\boldsymbol{E}\cdot d\boldsymbol{l}\\ =0+\int_r^{r_0}\frac{\lambda}{2\pi\varepsilon_0r}dr\\ =-\frac{\lambda}{2\pi\varepsilon_0}\ln r+\frac{\lambda}{2\pi\varepsilon_0}\ln r_0\\ =-\frac{\lambda}{2\pi\varepsilon_0}\ln r+C(r>R)\tag{29} uP=∫PP0E⋅dl=∫PP′E⋅dl+∫P′P0E⋅dl=0+∫rr02πε0rλdr=−2πε0λlnr+2πε0λlnr0=−2πε0λlnr+C(r>R)(29)
u P = ∫ P P 0 E ⋅ d l = ∫ r R E ⋅ d l + ∫ R r 0 E ⋅ d l = 0 + ∫ R r 0 λ 2 π ε 0 r d r = − λ 2 π ε 0 ln R + C ( r < R ) (30) u_P=\int_P^{P_0}\boldsymbol{E}\cdot d\boldsymbol{l}=\int_r^R\boldsymbol{E}\cdot d\boldsymbol{l}+\int_R^{r_0}\boldsymbol{E}\cdot d\boldsymbol{l}\\ =0+\int_R^{r_0}\frac{\lambda}{2\pi\varepsilon_0r}dr\\ =-\frac{\lambda}{2\pi\varepsilon_0}\ln R + C(r<R)\tag{30} uP=∫PP0E⋅dl=∫rRE⋅dl+∫Rr0E⋅dl=0+∫Rr02πε0rλdr=−2πε0λlnR+C(r<R)(30)
其中, C = λ 2 π ε 0 ln r 0 C=\frac{\lambda}{2\pi\varepsilon_0}\ln r_0 C=2πε0λlnr0
5.6 均匀带电球面电势
V ( r ) = { 1 4 π ε 0 q R ( r ≤ R ) 1 4 π ε 0 q r ( r > R ) (31) V(r) = \left\{ \begin{array}{c}\frac{1}{4\pi\varepsilon_0} \frac{q}{R} & (r \le R)\\\frac{1}{4\pi\varepsilon_0}\frac{q}{r}&(r>R)\end{array}\right.\tag{31} V(r)={4πε01Rq4πε01rq(r≤R)(r>R)(31)
5.7 均匀带电球体电势
球内距离球心 r r r处一点 P P P电势:
u = u 1 + u 2 = 1 4 π ε 0 Q R 3 r 2 + ∫ r R 1 4 π ε 0 d q 2 r ′ = 1 4 π ε 0 Q R 3 r 2 + ∫ r R 3 Q r ′ 4 π ε 0 R 3 d r ′ = Q ( 3 R 2 − r 2 ) 8 π ε 0 R 3 ( r < R ) (32) u = u_1+u_2=\frac{1}{4\pi\varepsilon_0}\frac{Q}{R^3}r^2+\int_r^R\frac{1}{4\pi\varepsilon_0}\frac{dq_2}{r'}\\ =\frac{1}{4\pi\varepsilon_0}\frac{Q}{R^3}r^2+\int_r^R\frac{3Qr'}{4\pi\varepsilon_0R^3}dr'\\ =\frac{Q(3R^2-r^2)}{8\pi\varepsilon_0R^3}(r<R)\tag{32} u=u1+u2=4πε01R3Qr2+∫rR4πε01r′dq2=4πε01R3Qr2+∫rR4πε0R33Qr′dr′=8πε0R3Q(3R2−r2)(r<R)(32)
球外距离球心 r r r处一点 P P P电势:
u = Q 4 π ε 0 r ( r ≥ R ) (33) u = \frac{Q}{4\pi\varepsilon_0r}(r\ge R)\tag{33} u=4πε0rQ(r≥R)(33)
注:在 P P P点的电场强度犹如电荷集中在球心处的点电荷在 P P P点产生的电场强度一样,故电势同理;
第六讲 电势与场强微分关系
E = − d u d n E l = − d u d l E = − ( ∂ u ∂ x i + ∂ u ∂ y j + ∂ u ∂ z k ) u ( x , y , z ) ⇒ E ( x , y , z ) (34) E = -\frac{du}{dn}\\ E_l=-\frac{du}{dl}\\ \boldsymbol{E}=-(\frac{\partial u}{\partial x}\boldsymbol{i}+\frac{\partial u}{\partial y}\boldsymbol{j}+\frac{\partial u}{\partial z}\boldsymbol{k})\\ u(x,y,z)\Rightarrow E(x,y,z)\tag{34} E=−dnduEl=−dlduE=−(∂x∂ui+∂y∂uj+∂z∂uk)u(x,y,z)⇒E(x,y,z)(34)
第七讲 静电场中的导体 电容
7.1 静电平衡导体表面
电场强度:
E = σ ε 0 n (35) \boldsymbol{E}=\frac{\sigma}{\varepsilon_0}\boldsymbol{n}\tag{35} E=ε0σn(35)
区别于无限大带电平面产生的电场(缺少静电平衡的条件):
E = σ 2 ε 0 n (36) \boldsymbol{E}=\frac{\sigma}{2\varepsilon_0}\boldsymbol{n}\tag{36} E=2ε0σn(36)
7.2 孤立导体电容
C = q u (37) C = \frac{q}{u}\tag{37} C=uq(37)
7.3 平行板电容器电容
C = q u 1 − u 2 = q E d = q σ ε 0 d = q q d ε 0 S = ε 0 S d (38) C = \frac{q}{u_1-u_2}\\ =\frac{q}{Ed}=\frac{q}{\frac{\sigma}{\varepsilon_0}d}\\ =\frac{q}{\frac{qd}{\varepsilon_0S}}=\frac{\varepsilon_0S}{d}\tag{38} C=u1−u2q=Edq=ε0σdq=ε0Sqdq=dε0S(38)
7.4 球形电容器电容
两球面间电场强度:
E = 1 4 π ε 0 q r 2 (39) E=\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}\tag{39} E=4πε01r2q(39)
u 1 − u 2 = ∫ R 1 R 2 E ⋅ d l = ∫ R 1 R 2 1 4 π ε 0 q r 2 d r = q 4 π ε 0 R 2 − R 1 R 1 R 2 ⇒ C = q u 1 − u 2 = 4 π ε 0 R 1 R 2 R 2 − R 1 (40) u_1-u_2=\int_{R_1}^{R_2}\boldsymbol{E}\cdot d\boldsymbol{l} = \int_{R_1}^{R_2}\frac{1}{4\pi\varepsilon_0}\frac{q}{r^2}dr\\ =\frac{q}{4\pi\varepsilon_0}\frac{R_2-R_1}{R_1R_2}\\ \Rightarrow C = \frac{q}{u_1-u_2}=\frac{4\pi\varepsilon_0R_1R_2}{R_2-R_1}\tag{40} u1−u2=∫R1R2E⋅dl=∫R1R24πε01r2qdr=4πε0qR1R2R2−R1⇒C=u1−u2q=R2−R14πε0R1R2(40)
7.5 电容器串并联
1 C = 1 C 1 + 1 C 2 + ⋅ ⋅ ⋅ + 1 C n ( 串联 ) C = C 1 + C 2 + ⋅ ⋅ ⋅ + C n ( 并联 ) (41) \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\cdot\cdot\cdot+\frac{1}{C_n}(串联)\\ C = C_1+C_2+\cdot\cdot\cdot+C_n(并联)\tag{41} C1=C11+C21+⋅⋅⋅+Cn1(串联)C=C1+C2+⋅⋅⋅+Cn(并联)(41)
第八讲 静电能
8.1 静电能公式推导
U ( t ) = q ( t ) C d A = U ( t ) d q = q ( t ) C d q A = ∫ d A = ∫ 0 Q q ( t ) C d q = Q 2 2 C Q = C U ⇒ A = 1 2 C U 2 = 1 2 Q U ⇒ W = A = Q 2 2 C = 1 2 C U 2 = 1 2 Q U (42) U(t) = \frac{q(t)}{C}\\dA = U(t)dq = \frac{q(t)}{C}dq\\ A = \int dA = \int_0^Q\frac{q(t)}{C}dq=\frac{Q^2}{2C}\\ Q=CU\Rightarrow A = \frac{1}{2}CU^2=\frac{1}{2}QU\\ \Rightarrow W=A=\frac{Q^2}{2C}=\frac{1}{2}CU^2=\frac{1}{2}QU\tag{42} U(t)=Cq(t)dA=U(t)dq=Cq(t)dqA=∫dA=∫0QCq(t)dq=2CQ2Q=CU⇒A=21CU2=21QU⇒W=A=2CQ2=21CU2=21QU(42)
8.2 电场能量密度推导
U = E d , C = ε 0 S d ⇒ W = 1 2 ε 0 E 2 S d = 1 2 ε 0 E 2 V ⇒ ω = W V = 1 2 ε 0 E 2 (43) U=Ed, C = \frac{\varepsilon_0S}{d}\\ \Rightarrow W = \frac{1}{2}\varepsilon_0E^2Sd = \frac{1}{2}\varepsilon_0E^2V\\ \Rightarrow \omega = \frac{W}{V}=\frac{1}{2}\varepsilon_0E^2\tag{43} U=Ed,C=dε0S⇒W=21ε0E2Sd=21ε0E2V⇒ω=VW=21ε0E2(43)
第九讲 电介质的极化 束缚电荷
9.1 电介质
C = ε r C 0 (44) C = \varepsilon_r C_0\tag{44} C=εrC0(44)
其中, ε r \varepsilon_r εr 称为介质的相对介电常数(相对电容率), C 0 C_0 C0 表示真空中对应的电容;因此,除真空中 ε r = 1 \varepsilon_r=1 εr=1 外,其余 ε r > 1 \varepsilon_r>1 εr>1;
9.2 介质极化
{ 有极分子 ⇒ 取向极化 无极分子 ⇒ 位移极化 \left\{\begin{array}{c}有极分子\Rightarrow 取向极化\\ 无极分子\Rightarrow 位移极化\end{array}\right. {有极分子⇒取向极化无极分子⇒位移极化
第十讲 电介质内的电场强度
根据电介质极化原理推导:
E = E 0 + E ′ E 0 = σ 0 ε 0 , E ′ = σ ′ ε 0 ⇒ E = σ 0 ε 0 − σ ′ ε 0 E = E 0 ε r ⇒ σ ′ = ( 1 − 1 ε r ) σ 0 (45) \boldsymbol{E} = \boldsymbol{E}_0+\boldsymbol{E}'\\ E_0=\frac{\sigma_0}{\varepsilon_0},E'=\frac{\sigma'}{\varepsilon_0}\\ \Rightarrow E = \frac{\sigma_0}{\varepsilon_0}-\frac{\sigma'}{\varepsilon_0}\\E = \frac{E_0}{\varepsilon_r}\\ \Rightarrow \sigma'=(1-\frac{1}{\varepsilon_r})\sigma_0\tag{45} E=E0+E′E0=ε0σ0,E′=ε0σ′⇒E=ε0σ0−ε0σ′E=εrE0⇒σ′=(1−εr1)σ0(45)
第十一讲 ★ \bigstar ★电介质中的高斯定理
11.1 电位移矢量
推导:
∬ S E ⋅ d S = 1 ε 0 ( σ 0 − σ ′ ) S 式 ( 45 ) ⇒ 1 ε 0 ( σ 0 − σ ′ ) = σ 0 ε 0 ε r ⇒ ∬ S ε 0 ε r E ⋅ d S = ε 0 S = q 0 令 D = ε E = ε 0 ε r E ⇒ ∬ S D ⋅ d S = q 0 (46) \iint_S\boldsymbol{E}\cdot d\boldsymbol{S}=\frac{1}{\varepsilon_0}(\sigma_0-\sigma')S\\ 式(45)\Rightarrow \frac{1}{\varepsilon_0}(\sigma_0-\sigma')=\frac{\sigma_0}{\varepsilon_0\varepsilon_r}\\ \Rightarrow \iint_S\varepsilon_0\varepsilon_r\boldsymbol{E}\cdot d\boldsymbol{S}=\varepsilon_0S=q_0\\ 令\boldsymbol{D} = \varepsilon\boldsymbol{E} = \varepsilon_0\varepsilon_r\boldsymbol{E}\\ \Rightarrow \iint_S\boldsymbol{D}\cdot d\boldsymbol{S} = q_0\tag{46} ∬SE⋅dS=ε01(σ0−σ′)S式(45)⇒ε01(σ0−σ′)=ε0εrσ0⇒∬Sε0εrE⋅dS=ε0S=q0令D=εE=ε0εrE⇒∬SD⋅dS=q0(46)
其中, D D D 称为电位移矢量或电通密度, ε = ε 0 ε r \varepsilon = \varepsilon_0\varepsilon_r ε=ε0εr 称为电介质的介电常数;
11.2 电介质中的能量密度
ω = 1 2 D ⋅ E ε r = 1 ⇒ ω = 1 2 ε 0 E 2 ( 真空中 ) (47) \omega = \frac{1}{2}\boldsymbol{D}\cdot\boldsymbol{E}\\ \varepsilon_r = 1\Rightarrow \omega = \frac{1}{2}\varepsilon_0E^2(真空中)\tag{47} ω=21D⋅Eεr=1⇒ω=21ε0E2(真空中)(47)
第十二讲 经典习题



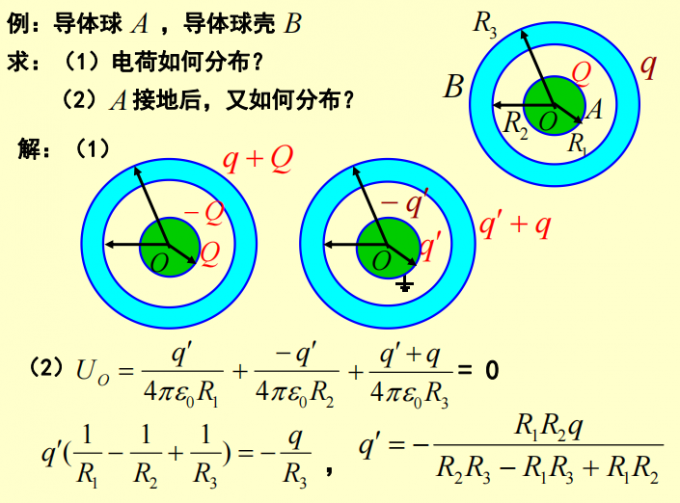
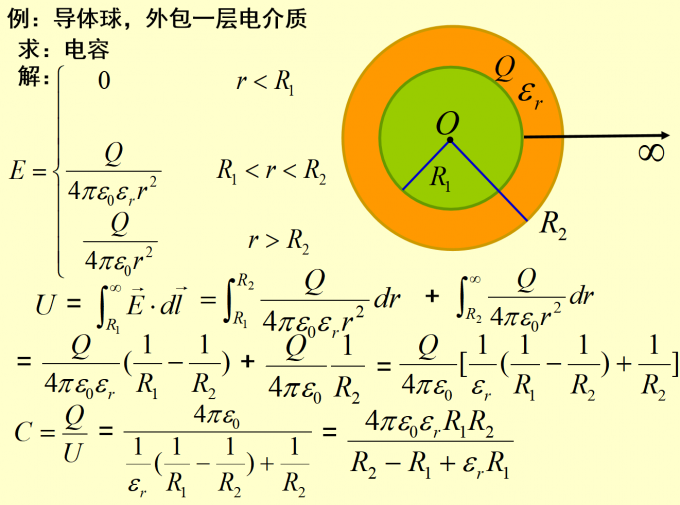






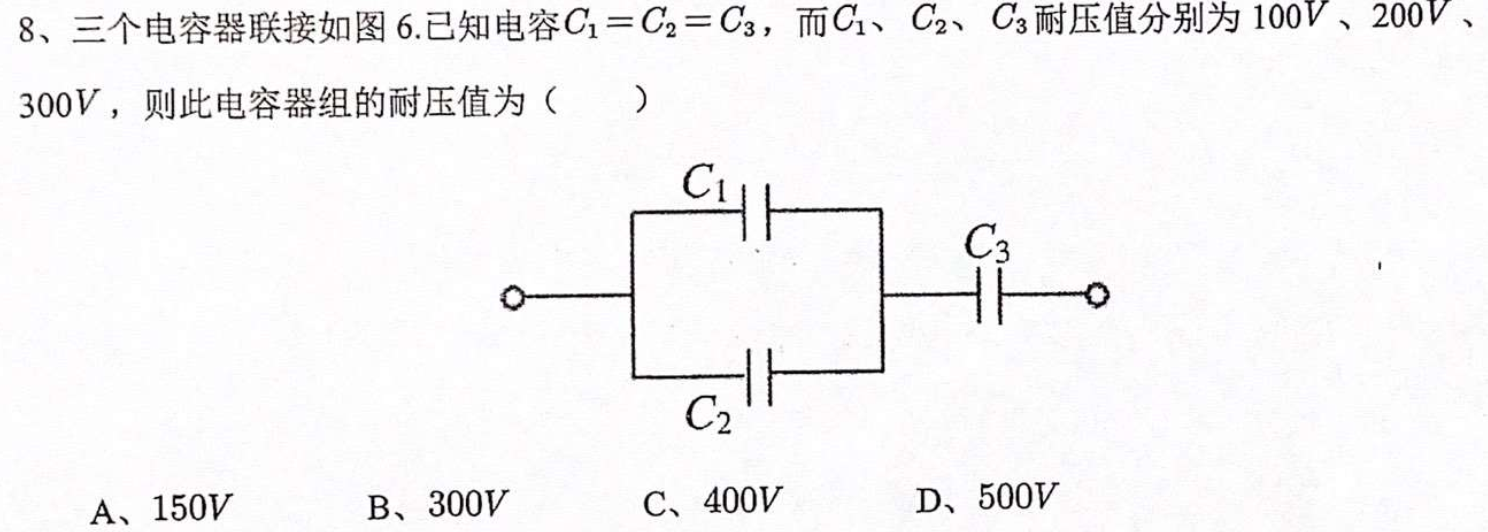


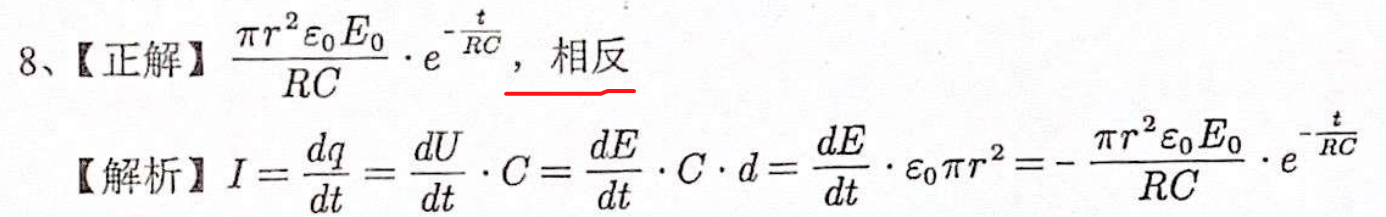
这篇关于西电计科院大学物理二期中复习笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







