第十二届蓝桥杯大赛软件类省赛C++研究生组

2023-10-10 05:40
文章标签 c++ 软件 蓝桥 研究生 大赛 第十二届 类省赛

本文主要是介绍第十二届蓝桥杯大赛软件类省赛C++研究生组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

  • A 卡片（5分，√）
  • B 直线（5分，√）
  • C 货物摆放（10分，√）
  • D 路径（10分，√）
  • E 回路计数（15分，√）
  • F时间显示（15分，√）
  • G砝码称重（20分，√）
  • H 异或数列（20分）
  • I 双向排序（25分）
  • J 分果果（25分）

题目是全的，但是由于能力有限，后面有题目没做，分值和完成情况在题目后说明

A 卡片（5分，√）

题目描述
本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。 小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个， 就保存起来，卡片就不能用来拼其它数了。 小蓝想知道自己能从 1 拼到多少。 例如，当小蓝有 30 张卡片，其中 0 到 9 各 3张，则小蓝可以拼出 1 到 10， 但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。 现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210 张，请问小蓝可以从 1 拼到多少？ 提示：建议使用计算机编程解决问题

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;int main()
{int arr[10] = {0};for(int i = 0; i < 10; i ++){arr[i] = 2021;}int minx = 2021;int n = 1;int flag;while(minx > 0){int m = n;while(m > 0 ){if(minx == 0){n --;break;}int tmp = m % 10;arr[tmp] -= 1;minx = min(minx, arr[tmp]);m /= 10;}n ++;}printf("%d\n", n);return 0;
}

B 直线（5分，√）

题目描述
在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上， 那么这些点中任意两点确定的直线是同一条。

给定平面上2×3个整点{(x,y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z}，即横坐标 是0到1 (包含0和1)之间的整数、纵坐标是0到2 (包含0和2)之间的整数 的点。这些点一共确定了 11 条不同的直线。

给定平面上20×21个整点{(x,y)|0 ≤ x < 20,0 ≤ y < 21,x ∈ Z,y ∈ Z}，即横 坐标是0到19 (包含0和19)之间的整数、纵坐标是0到20 (包含0和20)之 间的整数的点。请问这些点一共确定了多少条不同的直线。

利用两点式方程：(y - y1) / (x - x1) = (y2 - y1) / (x2 - x1)，化简后得：
y = [(y2 - y1) / (x2 - x1)] *x + (x1 * y2 - x2 * y1) / (x2 - x1),
从而得到斜率和截距。
注意：不能用y = kx + b，如：先用两点求出斜率k，再将斜率k和任一点带入求得b，这样会因为精度不准而导致结果错误。
int a = 6;
double b = 1.99;
double c = 1.999999999999;
double d = a * 1.0 / b;
double e = a * 1.0 / c;
cout << "a / b = " << d << “\n”; //3.01508
cout << "(a / b) * 3 = " << d * 3 << “\n”; // 9.04523
cout << "a / c = " << e << “\n”; //3
cout << "(a / c) * 3 = " << e * 3 << “\n”; //9

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;vector<pair<int, int>> all; //存放所有的点
set<pair<double, double>> res; //存放所有直线的斜率和截距int main()
{//获得所有的点for(int i = 0; i < 20; i ++){for(int j = 0; j < 21; j ++){all.push_back(make_pair(i, j));}}//每两个点组成一条直线for(int i = 0; i < all.size(); i ++){int x1 = all[i].first;int y1 = all[i].second;for(int j = 0; j < all.size(); j ++){int x2 = all[j].first;int y2 = all[j].second;if(x1 != x2){//确保分母不为0，即两点的x值不同double k = (y2 - y1) * 1.0 / (x2 - x1); //斜率double b = (x1 * y2 - x2 * y1) * 1.0 / (x2 - x1); //截距res.insert(make_pair(k, b));}}}//40257printf("%d\n", res.size() + 20); // 两点的x值相同的直线有20条（0<=x<20）return 0;
}

C 货物摆放（10分，√）

题目描述
小蓝有一个超大的仓库，可以摆放很多货物。

现在，小蓝有 nn 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、宽、高。

小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足 n=L×W×H。

给定 n，请问有多少种堆放货物的方案满足要求。

例如，当 n = 4 时，有以下 6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1。

请问，当 n = 2021041820210418 （注意有 16 位数字）时，总共有多少种方案？

提示：建议使用计算机编程解决问题。

答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;int main()
{long long n = 2021041820210418;int nn = int(pow(n, 1.0 / 2));long long arr[3000] = {0};int nums = 0;for(int i = 1; i <= nn; i ++){if(n % i == 0){arr[nums ++] = i;if(i != nn){arr[nums ++] = n / i;}}}int countn = 0;for(int i = 0; i < nums ;i ++){for(int j = 0; j < nums; j ++){for(int k = 0; k < nums; k ++){if(arr[i] * arr[j] * arr[k] == n){countn ++;}}}}printf("%d\n", countn);return 0;
}

D 路径（10分，√）

题目描述
本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图 中的最短路径。

小蓝的图由 2021 个结点组成，依次编号 1 至 2021。

对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点 之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。

例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无 向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。

请计算，结点 1 和结点 2021 之间的最短路径长度是多少。

提示：建议使用计算机编程解决问题。

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
int main()
{int arr[2025] = {0};memset(arr, 0x3f, sizeof(arr));arr[1] = 0;for(int i = 1; i <= 2021; i ++){for(int j = i + 1; j - i <= 21 && j <= 2021; j ++){arr[j] = min(arr[j], arr[i] + (i * j) / __gcd(i , j));}}printf("%d\n", arr[2021]);return 0;
}

E 回路计数（15分，√）

题目描述：
蓝桥学院由 2121​​​ 栋教学楼组成，教学楼编号 11​​ 到 2121​​。对于两栋教学楼 aa​​ 和 bb​，当 aa​ 和 bb​ 互质时，aa 和 bb 之间有一条走廊直接相连，两个方向皆可通行，否则没有直接连接的走廊。

小蓝现在在第一栋教学楼，他想要访问每栋教学楼正好一次，最终回到第一栋教学楼（即走一条哈密尔顿回路），请问他有多少种不同的访问方案？

两个访问方案不同是指存在某个 ii，小蓝在两个访问方法中访问完教学楼 ii 后访问了不同的教学楼。

提示：建议使用计算机编程解决问题。
答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;typedef long long ll;
const int all = 1 << 21;int arr[25][25] = {0};
ll dp[all][21] = {0};  //dp[x][i]:在x状态时，到达i栋楼的路径数int main()
{//若i, j最小公因数为1即两栋楼之间有通路，arr[i][j] = arr[j][i] = 1for(int i = 0; i < 21; i ++){for(int j = i + 1; j < 21; j ++){if( __gcd(i + 1, j + 1) == 1){arr[i][j] = arr[j][i] = 1;}}}dp[1][0] = 1;for(int x = 1; x < all; x ++){ //遍历所有情况//该情况下包括第0栋楼if(x & 1){for(int i = 0; i < 21; i ++){//某情况下包括第i栋楼if((x >> i) & 1){//与第i栋楼相连的楼for(int j = 0; j < 21; j ++){int tmp = x ^ (1 << i);//第i栋楼不在x状态下且j栋楼在x状态下，同时i与j之间有通路if((tmp >> j) & 1 & arr[i][j]){//到达i楼的路径数加经过j栋楼到达i的路径数dp[x][i] += dp[tmp][j];}}}}}}ll countn = 0;for(int i = 1; i < 21; i ++){if(arr[0][i]){countn += dp[all - 1][i];}}printf("%lld\n", countn);return 0;
}

F时间显示（15分，√）

题目描述
小蓝要和朋友合作开发一个时间显示的网站。

在服务器上，朋友已经获取了当前的时间，用一个整数表示，值为从 19701970 年 11 月 11 日 00:00:0000:00:00 到当前时刻经过的毫秒数。

现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要显示出时分秒即可，毫秒也不用显示，直接舍去即可。

给定一个用整数表示的时间，请将这个时间对应的时分秒输出。
输入
输入一行包含一个整数，表示时间。
输出
输出时分秒表示的当前时间，格式形如 HH:MM:SS，其中 HH 表示时，值为 00​​​​ 到 2323​​​​，MM 表示分，值为 00​​​​ 到 5959​​​，SS 表示秒，值为 00​​ 到 5959​。时、分、秒 不足两位时补前导 00。
样例：
输入1

46800999

输出1

13:00:00

输入2

1618708103123

输出2

01:08:23

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;int main()
{long long times;cin >> times;times /= 1000;times %= (24 * 60 * 60);int hh = times / (60 * 60);times %= (60 * 60);int mm = times / 60;int ss = times % 60;printf("%02d:%02d:%02d\n", hh, mm, ss);return 0;
}

G砝码称重（20分，√）

题目描述
你有一架天平和 N 个砝码，这 N 个砝码重量依次是W1、W2……Wn。请你计算一共可以称出多少种不同的重量？ 注意砝码可以放在天平两边。
输入
输入的第一行包含一个整数 NN。
第二行包含 N 个整数：W1,W2,W3……，Wn
输出
输出一个整数代表答案。
样例
输入：

3
1 4 6

输出

10

解释：
能称出的 10 种重量是：1、2、3、4、5、6、7、9、10、11。

1 = 1；
2 = 6 − 4 (天平一边放 6，另一边放 4)；​
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
9 = 4 + 6 − 1；
10 = 4 + 6；
11 = 1 + 4 + 6。

前i个砝码能组成的j重量的方案数，其实大于1即可，分三种情况：
1、前i-1个就可以达到重量j；
2、第i个才能达到重量j，则前i-1个只能达到重量j-arr[i];
3、前i-1个可达到j+arr[j];

#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;int arr[105] = {0};
int dp[105][100005] = {0};int main()
{int n;scanf("%d", &n);int sumn = 0;for(int i = 1; i <= n; i ++){scanf("%d", &arr[i]);sumn += arr[i];}dp[0][0] = 1;for(int i = 1; i <= n; i ++){for(int j = 0; j <= sumn; j ++){dp[i][j] = dp[i - 1][j] + dp[i - 1][ j + arr[i]] + dp[i - 1][abs(j - arr[i])];}}int countn = 0;for(int i = 1; i <= sumn; i ++){if(dp[n][i]){countn ++;}}printf("%d\n", countn);return 0;
}

H 异或数列（20分）

题目描述
Alice 和 Bob 正在玩一个异或数列的游戏。初始时，Alice 和 Bob 分别有一个整数 a 和 b，初始值均为 0。

有一个给定的长度为 nn​​的公共数列 X1,X2,……，Xn​​。Alice 和 Bob 轮流操作，Alice 先手，每步可以在以下两种选项中选一种：

选项 1：从数列中选一个Xi给 Alice 的数异或上，或者说令 a⊕Xi ​​。（其中⊕​​ 表示按位异或）;
选项 2：从数列中选一个Xi给 Bob 的数异或上，或者说令 b​​ 变为 b ⊕Xi​​。

每个数 Xi都只能用一次，当所有 Xi均被使用后（n​​ 轮后）游戏结束。游戏结束时，拥有的数比较大的一方获胜，如果双方数值相同，即为平手。 现在双方都足够聪明，都采用最优策略，请问谁能获胜？
输入描述
每个评测用例包含多组询问。询问之间彼此独立。
输入的第一行包含一个整数 T，表示询问数。
接下来 T​ 行每行包含一组询问。其中第 i​ 行的第一个整数 ni表示数列长度，随后 ni个整数 X1, X2, …… , Xni表示数列中的每个数。
输出描述
输出 T​​ 行，依次对应每组询问的答案。每行包含一个整数 1​​、0​ 或−1 分别表示 Alice 胜、平局或败。
样例
输入

4
1 1
1 0
2 2 1
7 992438 1006399 781139 985280 4729 872779 563580

输出

1
0
1
1

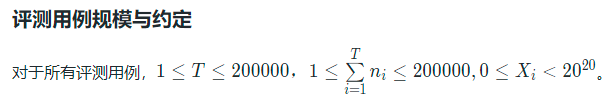
在这里插入图片描述

I 双向排序（25分）

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

J 分果果（25分）

题目描述
小蓝要在自己的生日宴会上将 n​​​​ 包糖果分给 m​​​​ 个小朋友。每包糖果都要分出去，每个小朋友至少要分一包，也可以分多包。

小蓝已经提前将糖果准备好了，为了在宴会当天能把糖果分得更平均一些，小蓝要先计算好分配方案。 小蓝将糖果从 1​​​ 到 nn​编号，第 i​ 包糖果重 wi。小朋友从 1 到 m​​ 编号。每个小朋友只能分到编号连续的糖果。小蓝想了很久没想出合适的分配方案使得每个小朋友分到的糖果差不多重。因此需要你帮他一起想办法。为了更好的分配糖果，他可以再买一些糖果，让某一些编号的糖果有两份。当某个编号的糖果有两份时，一个小朋友最多只能分其中的一份。

请找一个方案，使得小朋友分到的糖果的最大重量和最小重量的差最小，请输出这个差。

例如，小蓝现在有 5​​​​ 包糖果，重量分别为 6, 1, 2, 7, 9，如果小蓝要分给两个小朋友，则他可以将所有糖果再买一份，两个小朋友都分到 11​​​ 至 55​​ 包糖果，重量都是 25​，差为 0。

再如，小蓝现在有 55​​​​​​​ 包糖果，重量分别为 6, 1, 2, 7, 9，如果小蓝要分给三个小朋友，则他可以将第 3 包糖果再买一份，第一个小朋友分 1​​​​​​ 至 33​​​​ 包，第二个小朋友分 3​​​​ 至 4​​​ 包，第三个小朋友分第 5​​ 包，每个小朋友分到的重量都是 9​，差为 0。

再如，小蓝现在有 5​ 包糖果，重量分别为 6, 1, 2, 7, 9，如果小蓝要分给四个小朋友，则他可以将第 3 包和第 5 包糖果再买一份，仍然可以每个小朋友分到的重量都是 9，差为 0。

再如，小蓝现在有 5​​​​​​​​​​​​​ 包糖果，重量分别为 6, 1, 2, 7, 9​​​​​​​​​​​​，如果小蓝要分给五个小朋友，则他可以将第 4 包和第 5​​​​​​​​​​​ 包糖果再买一份，第一个小朋友分第 1​​​​​​​​​​ 至 2​​​​​​​​​ 包重量为 7​​​​​​​​，第二个小朋友分第 3​​​​​​​ 至 4​​​​​​ 包重量为 9​​​​​，第三个小朋友分第 4​​​​ 包重量为 7​​​，第四个和第五个小朋友都分第 5​​ 包重量为 9​。差为 2。
输入描述
输入第一行包含两个整数 n 和 m，分别表示糖果包数和小朋友数量。
第二行包含 n 个整数 w1, w2, · · · , wn ，表示每包糖果的重量。
输出描述
输出一个整数，表示在最优情况下小朋友分到的糖果的最大重量和最小重量的差。
样例
输入1：

5 2
6 1 2 7 9

输出1

0

输入2：

5 5
6 1 2 7 9

输出2

2

在这里插入图片描述

这篇关于第十二届蓝桥杯大赛软件类省赛C++研究生组的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/178332。

相关文章

C#如何调用C++库

C#如何调用C++库

《C#如何调用C++库》：本文主要介绍C#如何调用C++库方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录方法一：使用P/Invoke1. 导出C++函数2. 定义P/Invoke签名3. 调用C++函数方法二：使用C++/CLI作为桥接1. 创建C++/CL
阅读更多...
C++如何通过Qt反射机制实现数据类序列化

C++如何通过Qt反射机制实现数据类序列化

《C++如何通过Qt反射机制实现数据类序列化》在C++工程中经常需要使用数据类,并对数据类进行存储、打印、调试等操作,所以本文就来聊聊C++如何通过Qt反射机制实现数据类序列化吧... 目录设计预期设计思路代码实现使用方法在 C++ 工程中经常需要使用数据类，并对数据类进行存储、打印、调试等操作。由于数据类
阅读更多...
Linux下如何使用C++获取硬件信息

Linux下如何使用C++获取硬件信息

《Linux下如何使用C++获取硬件信息》这篇文章主要为大家详细介绍了如何使用C++实现获取CPU,主板,磁盘,BIOS信息等硬件信息,文中的示例代码讲解详细,感兴趣的小伙伴可以了解下... 目录方法获取CPU信息：读取"/proc/cpuinfo"文件获取磁盘信息：读取"/proc/diskstats"文
阅读更多...
C++使用printf语句实现进制转换的示例代码

C++使用printf语句实现进制转换的示例代码

《C++使用printf语句实现进制转换的示例代码》在C语言中,printf函数可以直接实现部分进制转换功能,通过格式说明符（formatspecifier）快速输出不同进制的数值,下面给大家分享C+... 目录一、printf 原生支持的进制转换1. 十进制、八进制、十六进制转换2. 显示进制前缀3. 指
阅读更多...
C++中初始化二维数组的几种常见方法

C++中初始化二维数组的几种常见方法

《C++中初始化二维数组的几种常见方法》本文详细介绍了在C++中初始化二维数组的不同方式,包括静态初始化、循环、全部为零、部分初始化、std::array和std::vector,以及std::vec... 目录1. 静态初始化2. 使用循环初始化3. 全部初始化为零4. 部分初始化5. 使用 std::a
阅读更多...
C++ vector的常见用法超详细讲解

C++ vector的常见用法超详细讲解

《C++vector的常见用法超详细讲解》：本文主要介绍C++vector的常见用法,包括C++中vector容器的定义、初始化方法、访问元素、常用函数及其时间复杂度,通过代码介绍的非常详细,... 目录1、vector的定义2、vector常用初始化方法1、使编程用花括号直接赋值2、使用圆括号赋值3、ve
阅读更多...
如何高效移除C++关联容器中的元素

如何高效移除C++关联容器中的元素

《如何高效移除C++关联容器中的元素》关联容器和顺序容器有着很大不同,关联容器中的元素是按照关键字来保存和访问的,而顺序容器中的元素是按它们在容器中的位置来顺序保存和访问的,本文介绍了如何高效移除C+... 目录一、简介二、移除给定位置的元素三、移除与特定键值等价的元素四、移除满足特android定条件的元
阅读更多...
Python获取C++中返回的char*字段的两种思路

Python获取C++中返回的char*字段的两种思路

《Python获取C++中返回的char*字段的两种思路》有时候需要获取C++函数中返回来的不定长的char*字符串,本文小编为大家找到了两种解决问题的思路,感兴趣的小伙伴可以跟随小编一起学习一下... 有时候需要获取C++函数中返回来的不定长的char*字符串，目前我找到两种解决问题的思路，具体实现如下：
阅读更多...
C++ Sort函数使用场景分析

C++ Sort函数使用场景分析

《C++Sort函数使用场景分析》sort函数是algorithm库下的一个函数,sort函数是不稳定的,即大小相同的元素在排序后相对顺序可能发生改变,如果某些场景需要保持相同元素间的相对顺序,可使... 目录C++ Sort函数详解一、sort函数调用的两种方式二、sort函数使用场景三、sort函数排序
阅读更多...
Java调用C++动态库超详细步骤讲解(附源码)

Java调用C++动态库超详细步骤讲解(附源码)

《Java调用C++动态库超详细步骤讲解(附源码)》C语言因其高效和接近硬件的特性,时常会被用在性能要求较高或者需要直接操作硬件的场合,：本文主要介绍Java调用C++动态库的相关资料,文中通过代... 目录一、直接调用C++库第一步：动态库生成（vs2017+qt5.12.10）第二步：Java调用C++
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2