几种常见的大O记法

1. O(1):

1.1定义：O(1)，意为一种算法无论面对多大的数据量，其步数总是相同的；
1.2举例：就像无论数组有多大，读取元素都只要1步；
也如数据末尾的删除与插入，无论数据有多大，这两种操作都只需1步，
所以它们的效率都是O(1).

2.O(N):

1.1定义:O(N)，对于N个元素的数据，线性查找需要花N步，即为O(N)

3.常数时间与线性时间

 3.1常数时间：不管数据量多少，算法的步数都是恒定的；所以O(1)也被成为常数时间3.2线性时间：于O(N)来讲，数据越多，算法所需的步数就越多，所以O(N)也被成为线性时间

注意：

O(1)还是O(N)高效，答案并不固定，而是通过数据的大小来确定的，如上图所示；
当数据值小于临界点时，O(N)所用步数更少，当处于临界点时，二者所用步数相同，
当大于临界点时，O(1)所用步数更少。

4.O(logN)

4.1定义：

    简单来说，O(logN)意味着，该算法当数据量翻倍时，步数加1；二分查找比线性查找要快。它不能写成O(1),因为二分查找的步数会随着数据量 的增长而增长；它也不能写成O(logN),因为步骤比元素数量要少，二分查找的 时间复杂度介于O(1)和O(N)之间，他们的时间复杂度较为对数时间；

4.2对数:

对数是指数的反函数，所以我们先回顾一下指数。
2的3次方等于：
2×2×2
结果为8。
log2 8则将上述计算反过来，它意思是：要把2乘以自身多少次，才能得到8。
因为需要3次，所以，log2 8=3。
log28可以表达为：将8不断地除以2直到1，需要多少个2。
8 / 2 / 2 / 2=1（注：按照从左到右的顺序计算。）
或者说，将8不断地除以2，要除多少次才能到1呢？答案是3，所以，log2 8=3。

5.对数时间

每次数据量翻倍时，O(N)算法的步数也跟着翻倍，O(log N)算法却只需加1。
5-1下图为O(logN)步数和O(N)步数岁数据量变化对比

5-2下图为对数时间与线性时间和常量时间随元素数量变化对比

6.O(N²) 冒泡排序

6.1定义：
冒泡排序是一种很基本的排序算法，步骤如下：
（1）指向指数中两个相邻的元素，比较他们的大小
（2）如果他们的顺序错了（即左边的值大于右边的值），就互换位置；顺序是正确
的就不做变动
（3）将两个指针右移一格
（4）重复（1）至（3）步，直至从头到尾都无需在做交换6.2效率：冒泡排序的執行步骤可分为两种a.比较：比较两个数看哪个更大b.交换：交换两个数的位置以使它们按顺序排列

7.0二次时间

 右下图可知，随着N的增长，步数大约增长N²，O(N²)也被叫做二次时间

8.选择排序

 	8.1 选择排序：（1）从左至右逐个遍历每个元素，选出最小的那个，记下索引（2）将最小元素值与本次遍历的起点元素值交换，以此类推（3）遍历起点+1，重复（1）（2）步骤，直至数组排好序

8.2选择排序实现
以下是javascript实现步骤

function selectionSort(array) {for(var i=0; i < array.length; i++) {var lowestNumberIndex=i;for(var j=i + 1; j < array.length; j++) {if(array[j] < array[lowestNumberIndex]) {lowestNumberIndex=j;}}if(lowestNumberIndex !=i) {var temp=array[i];array[i]=array[lowestNumberIndex];array[lowestNumberIndex]=temp;}}return array;}

8.3选择排序效率
下表为冒泡排序和选择排序的并列对比：

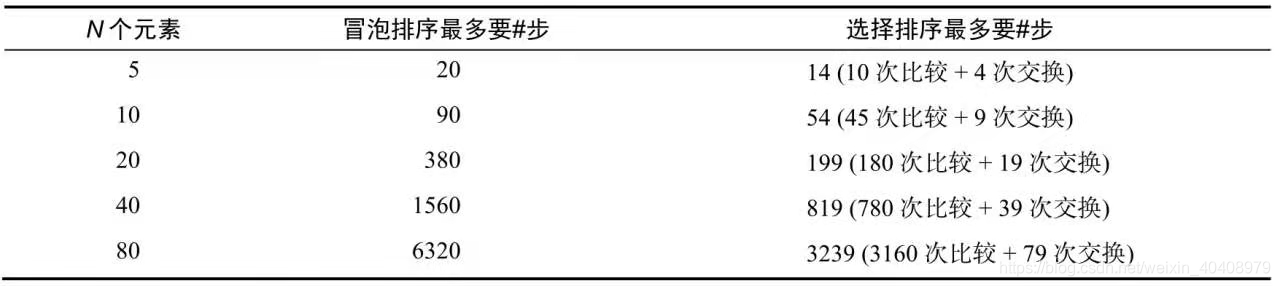
从表中可以清晰的看到，选择排序的步数大概是冒泡排序的一半，即选择排序比冒泡排序快一倍。
注意：
虽然选择排序的效率比冒泡排序快一倍，但是大O记法中，选择排序的效率也是0(N²)来表示，以为大O记法中有一条规则是 忽略常数**