王佩丰Excel24讲_第17讲：数学函数

一、认识函数

1.round、roundup、rounddown、int函数

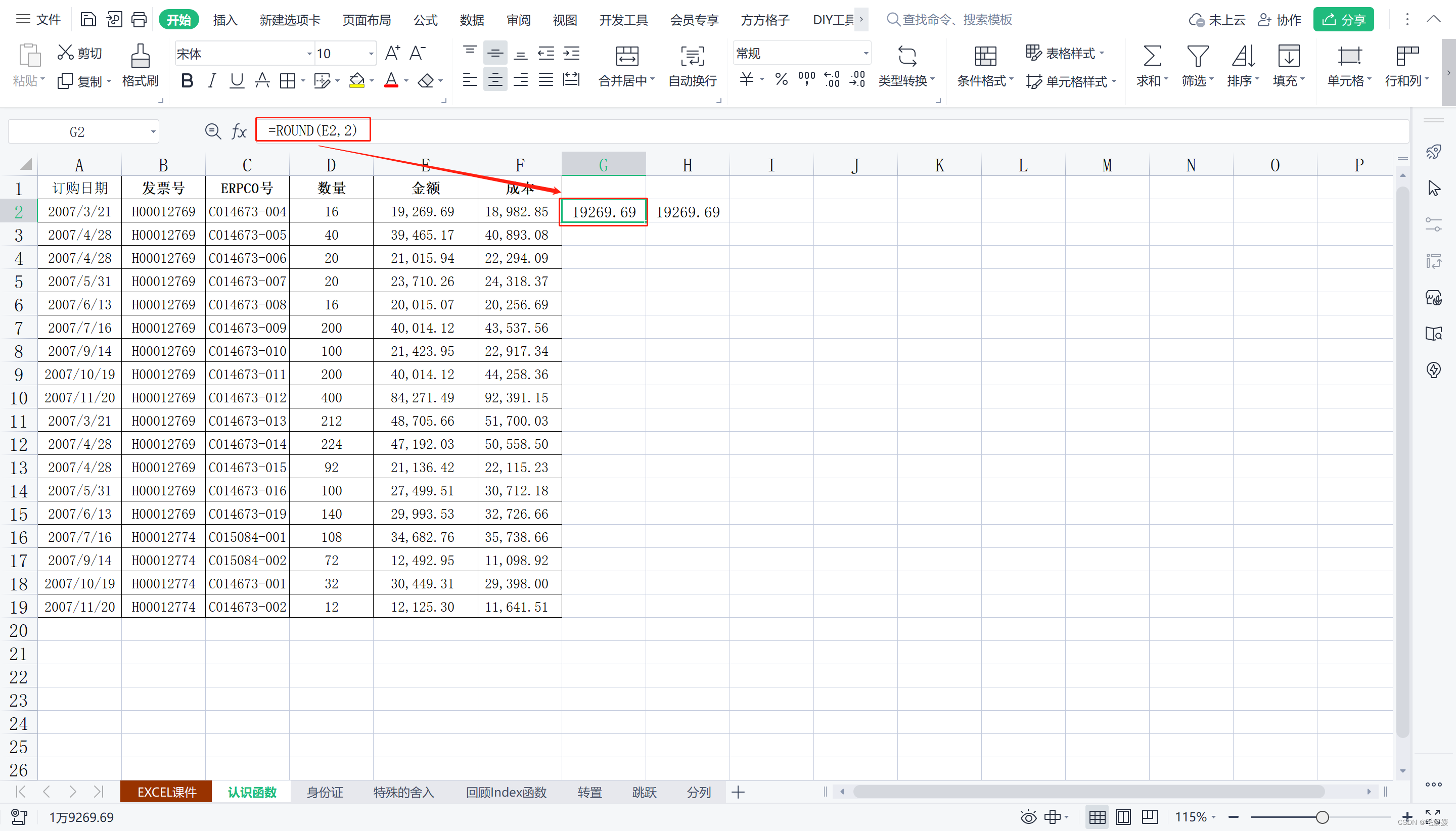
ROUND(数值,小数位数)
返回某个数字按指定位数取整后的数字

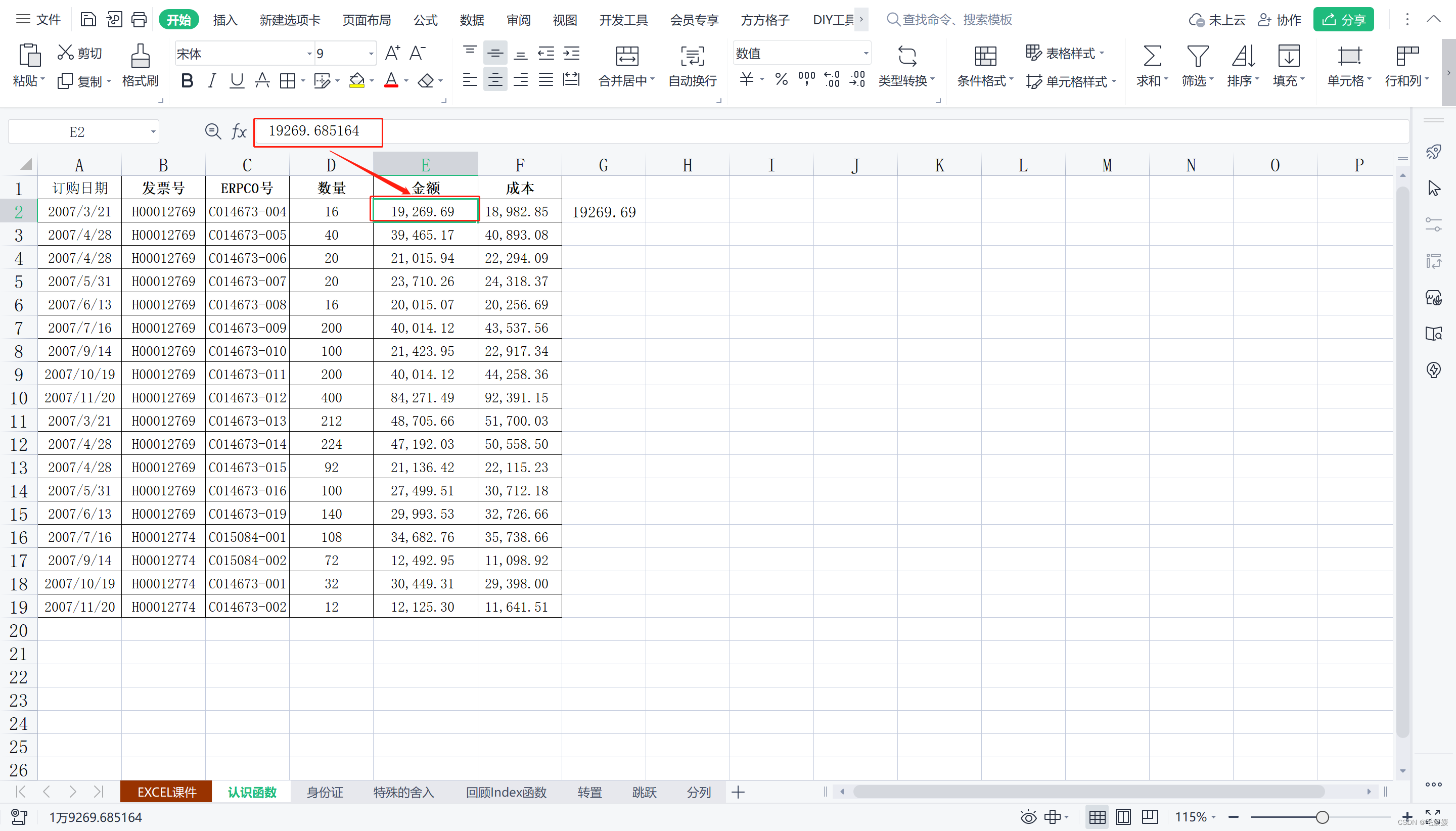
原数据看起来保留2位小数，实际上是6位，只是格式展示为2位；而使用round()函数之后，发现确实实现了保留2位小数。

ROUNDUP(数值,小数位数)
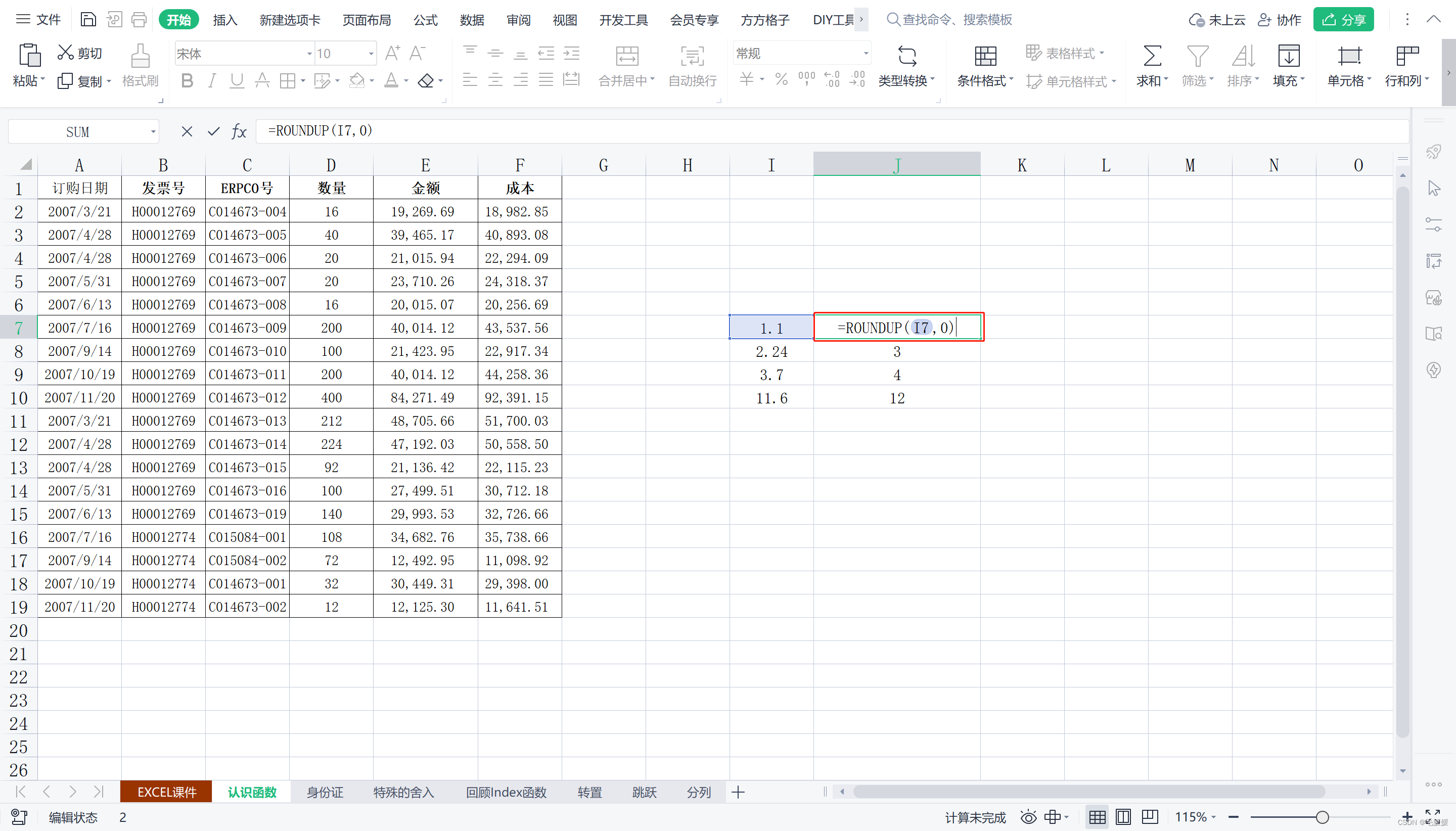
向上（绝对值增大的方向）舍入数字

比如“计算人力成本”，向上取

ROUNDDOWN(数值,小数位数)
向下（绝对值减小的方向）舍入数字

比如“计算调休休假”，向下取

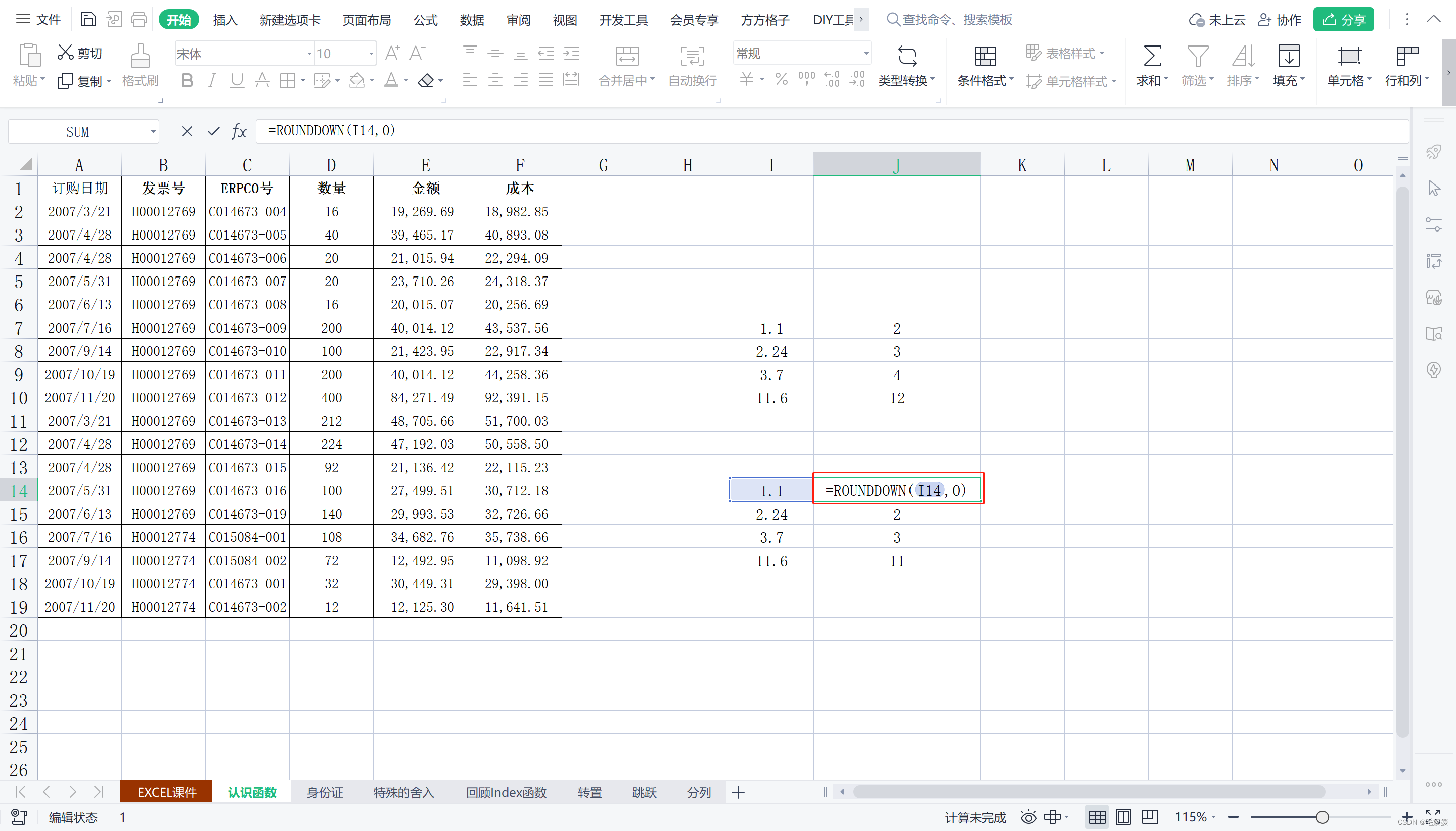
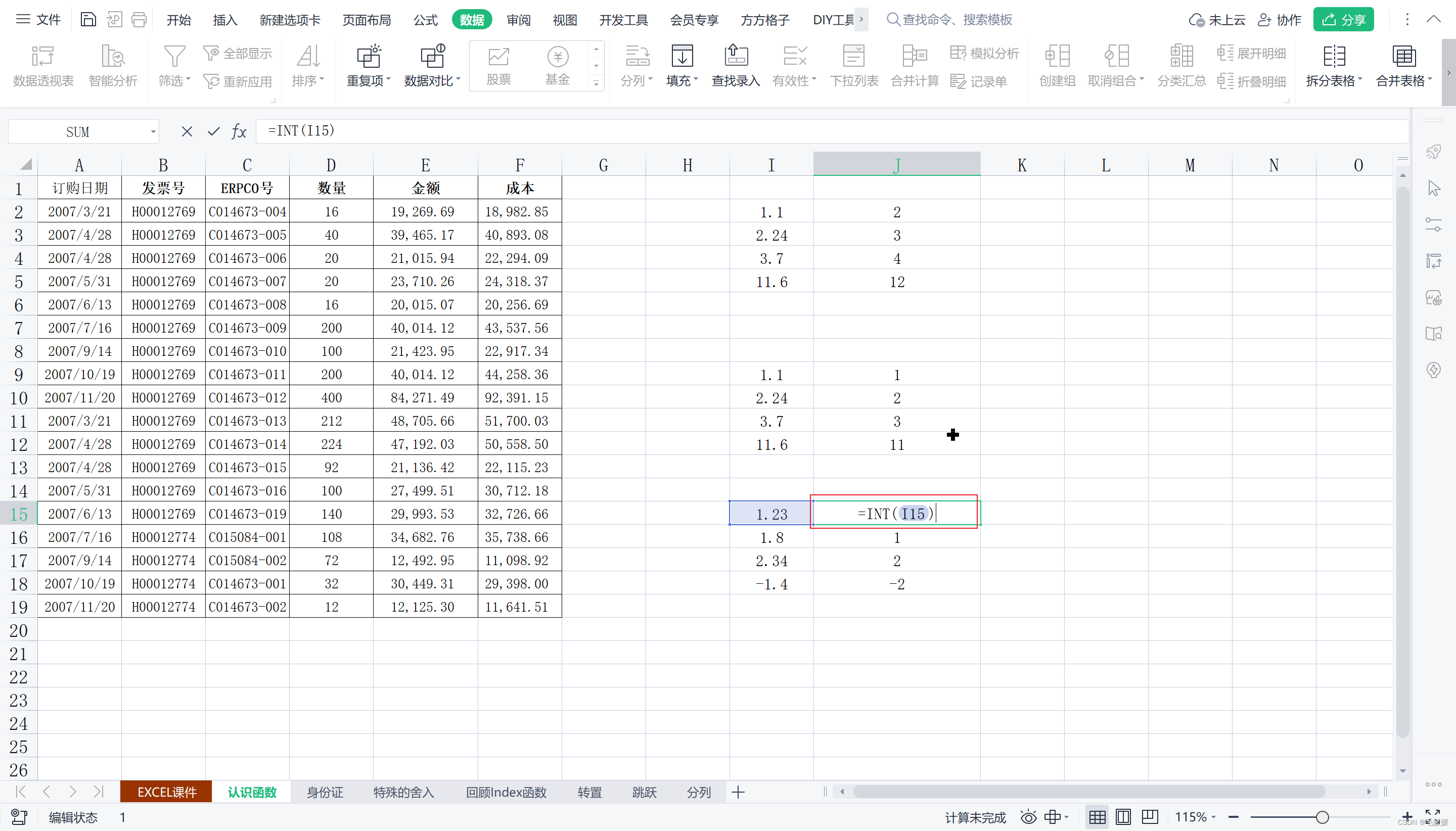
INT(数值)
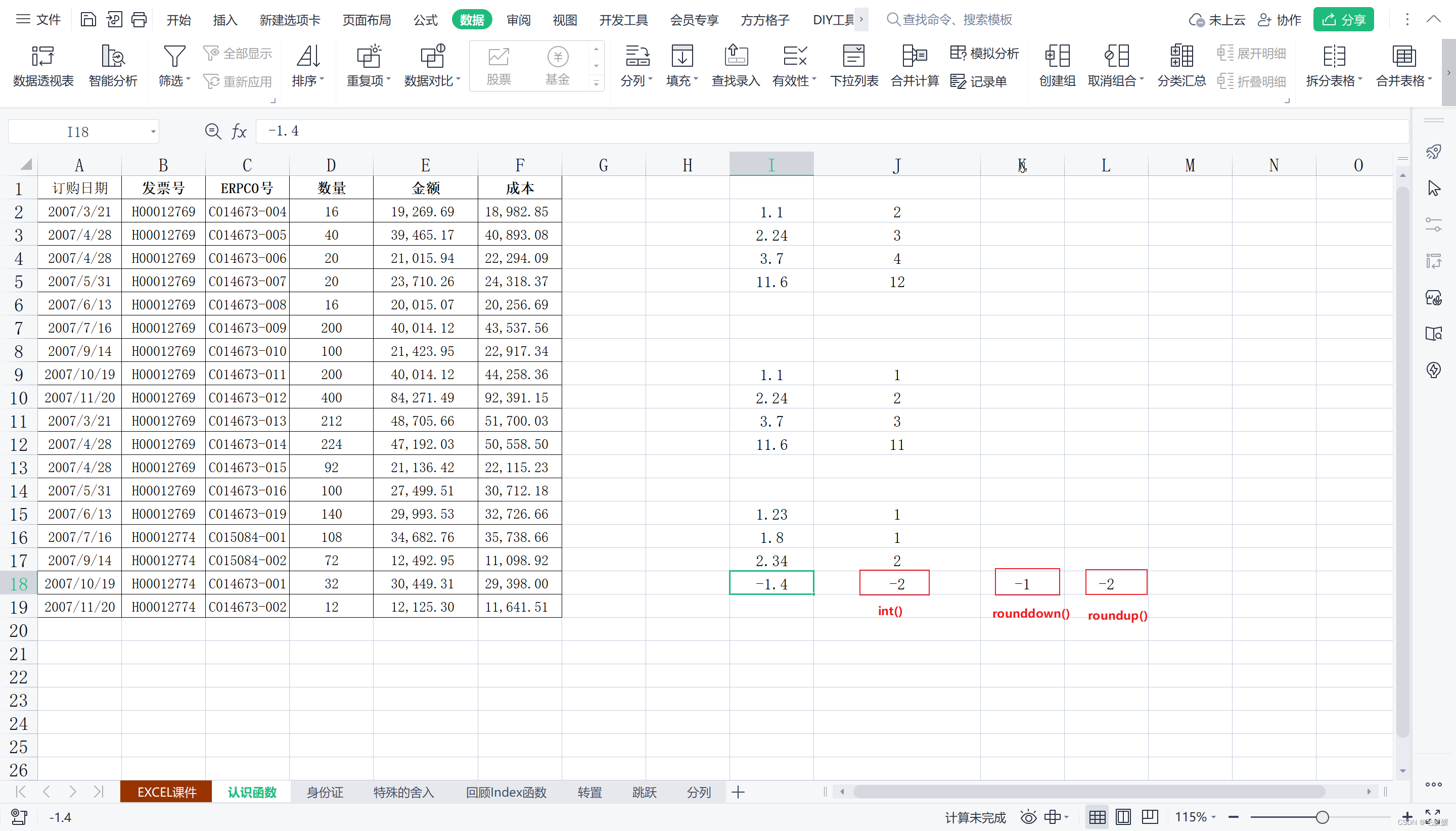
将数字向下舍入到最接近的整数

在处理正数的时候，int()函数与rounddown()函数用法一样；但在处理负数的时候，int()函数与roundup()函数用法一样。

2.mod函数

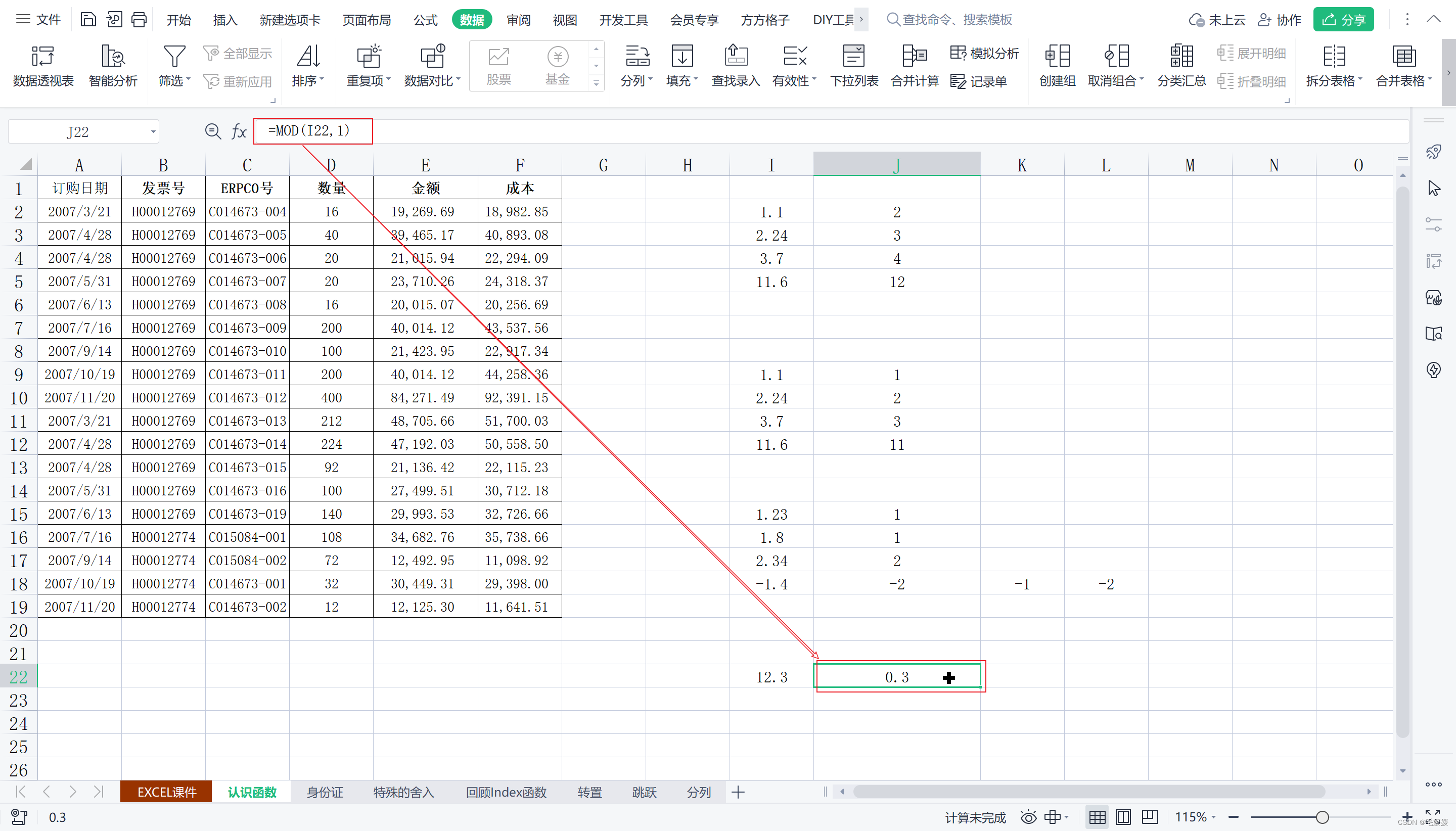
MOD(数值,除数)
返回两数相除的余数，结果的正负号与除数相同

如果想得到一个数字的小数部分，可以用mod(数值,1)；
任何整数除以2得到的余数，要么是0要么是1

3.row函数与column函数

ROW([参照区域])
返回指定引用的行号

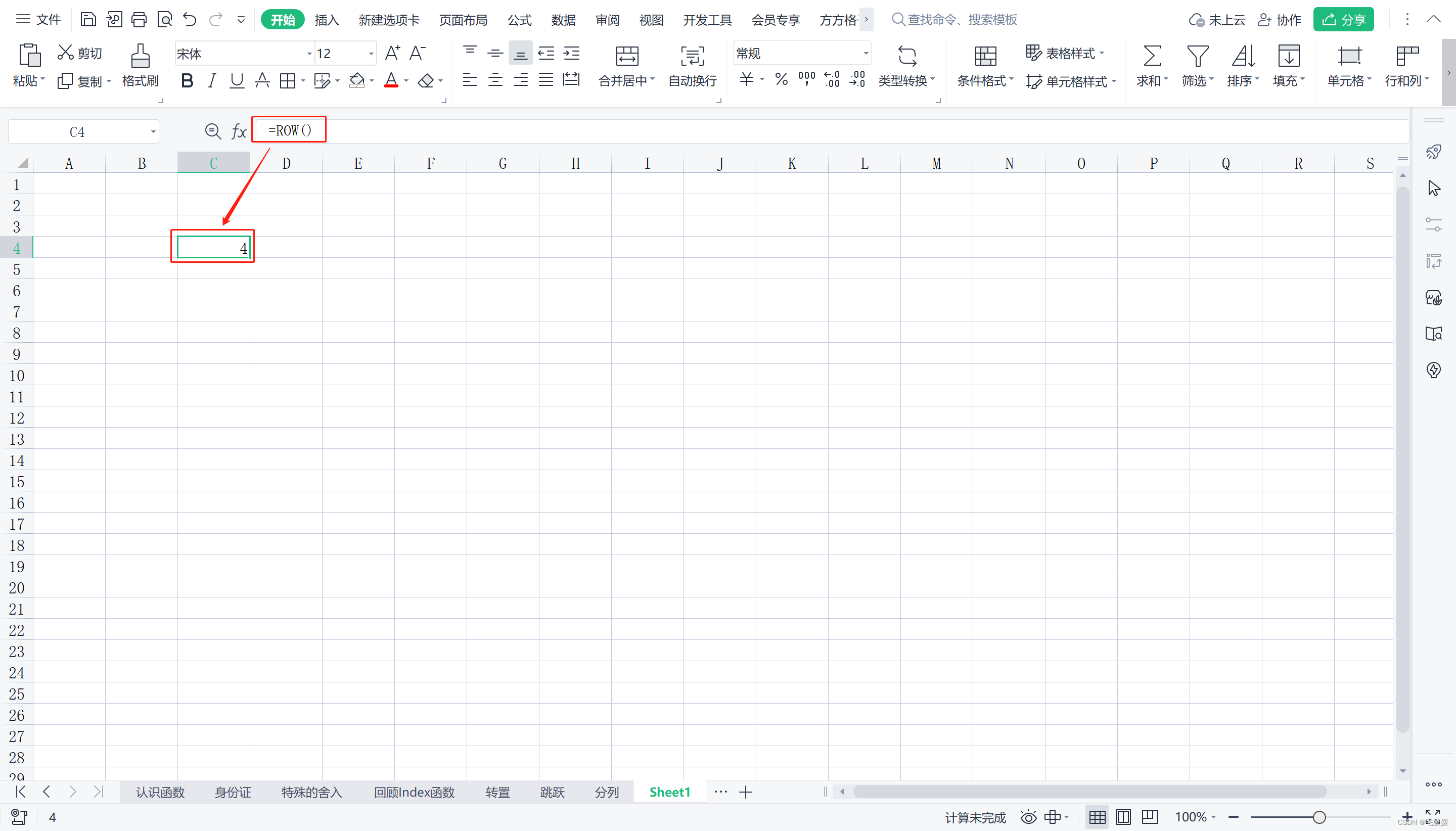
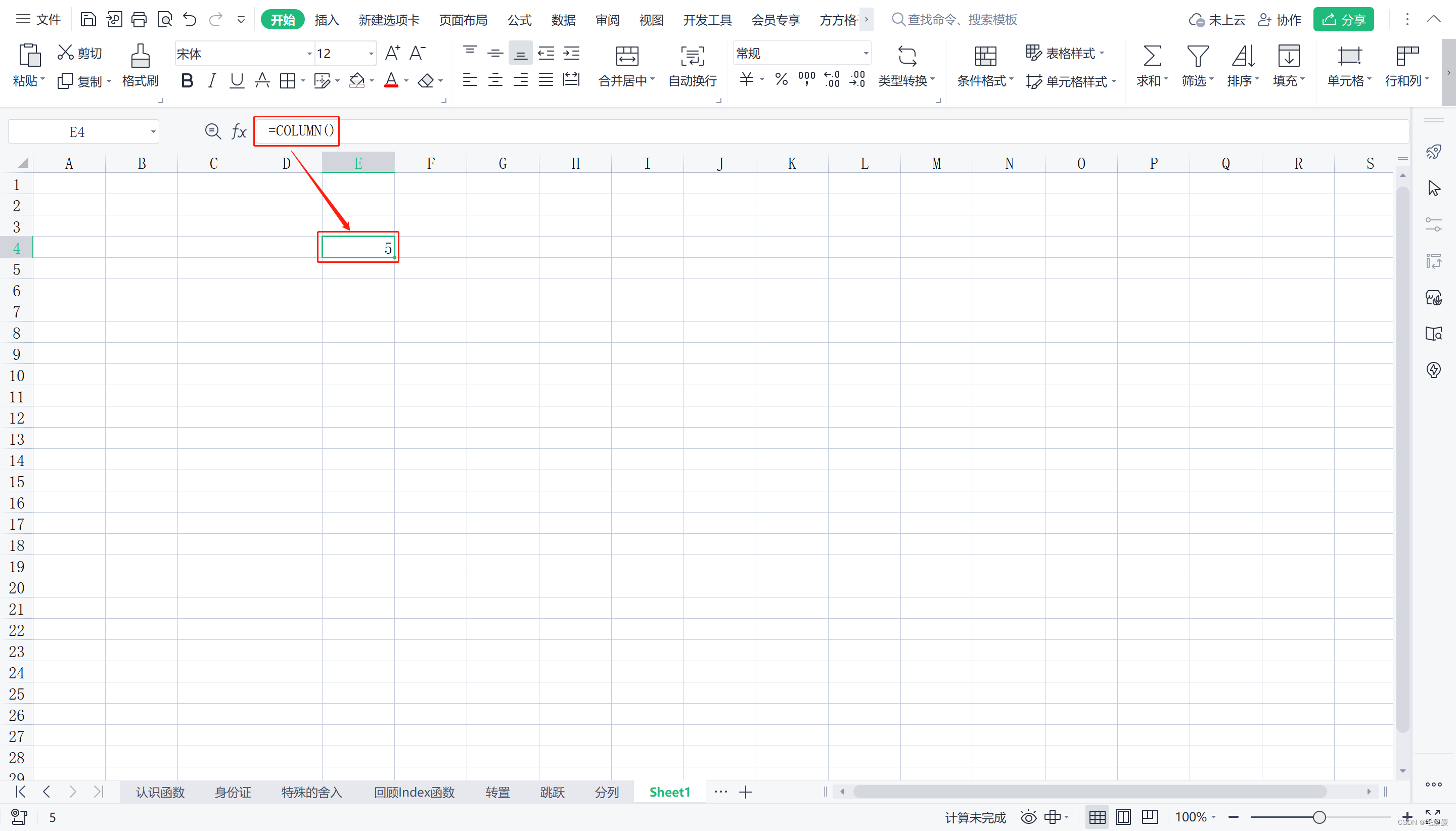
COLUMN([参照区域])
返回指定引用的列号

二、函数应用实例

1.通过身份证号码判断性别

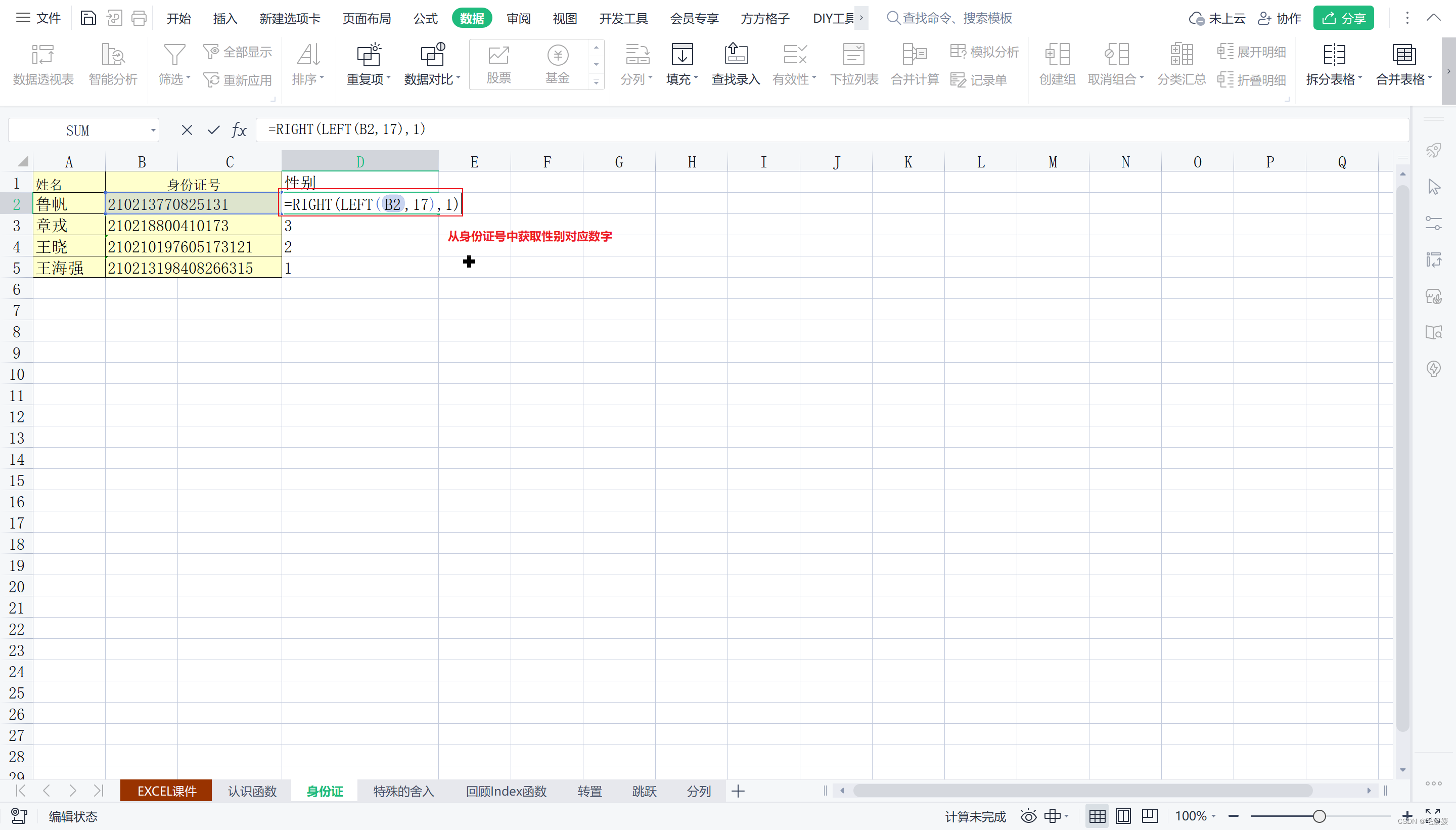
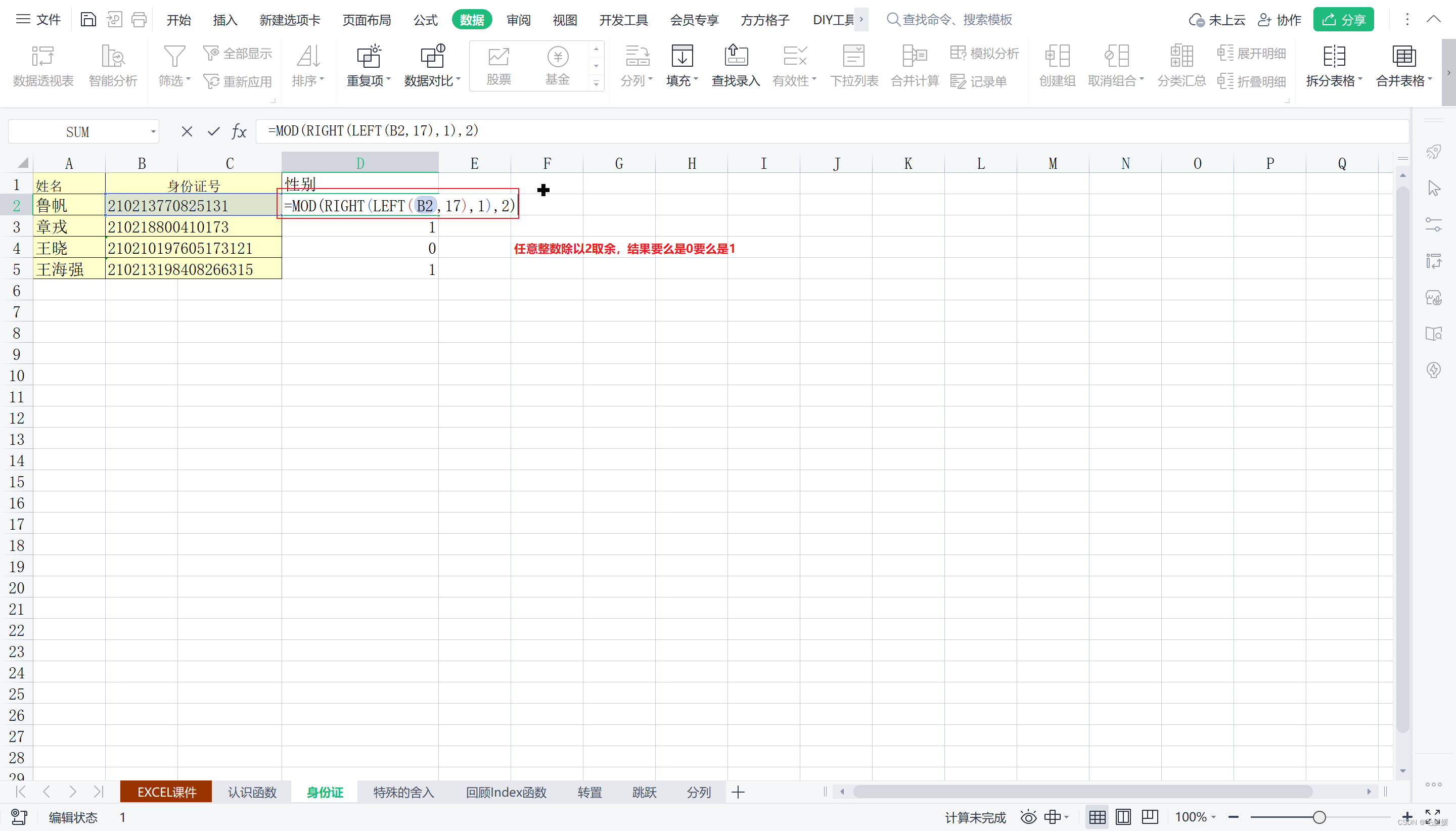
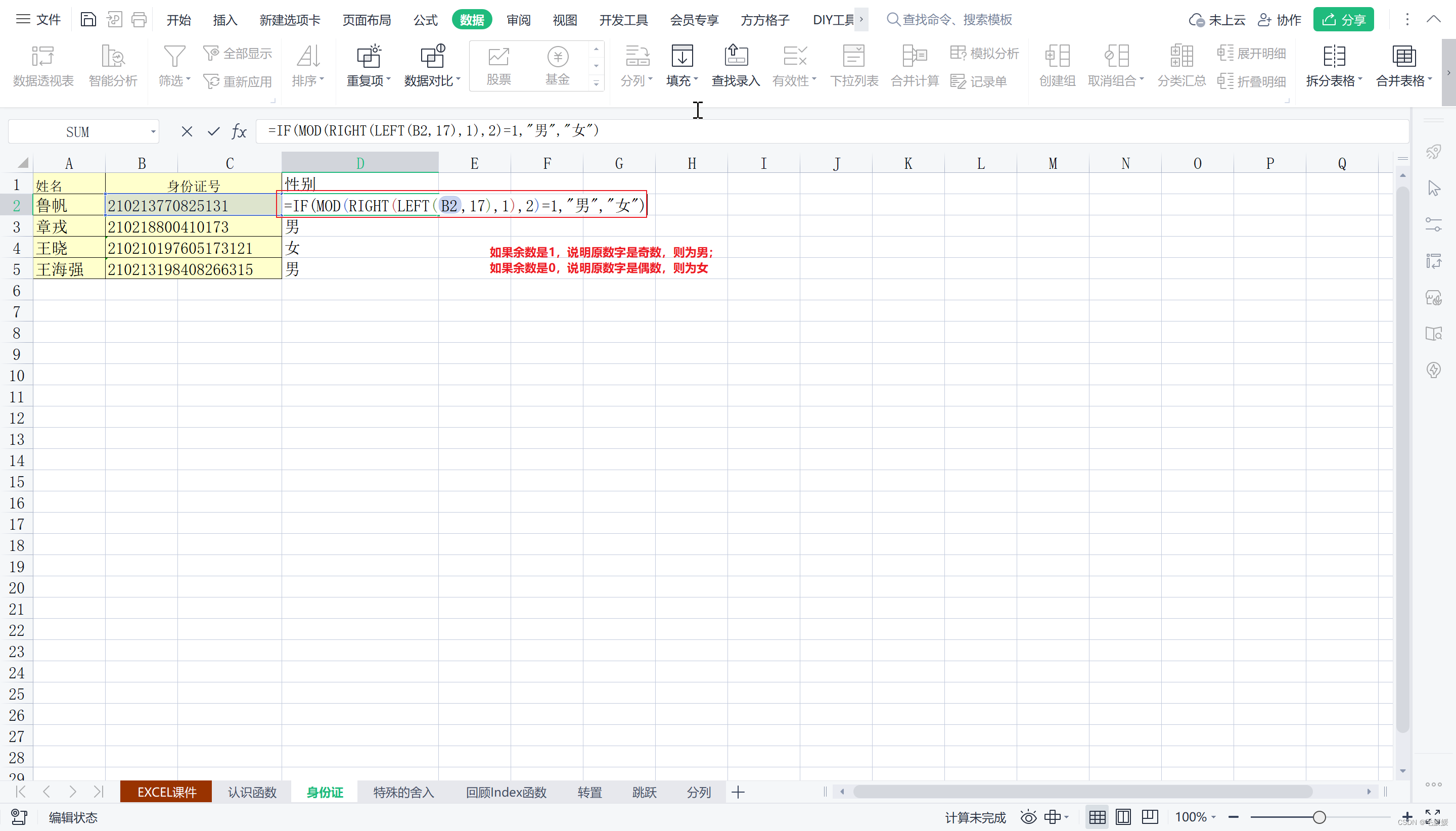
2.特殊的舍入方式–员工假期计算

小数部分超过0.5，取整数部分，再加上0.5；小数部分不超过0.5，只取整数部分
0和0.5是任意一个整数除以2之后的两种结果，要不除得尽小数部分为0，要么除不尽小数部分是0.5；
因此“实际调休天数”一定是某个整数除以2之后的结果；

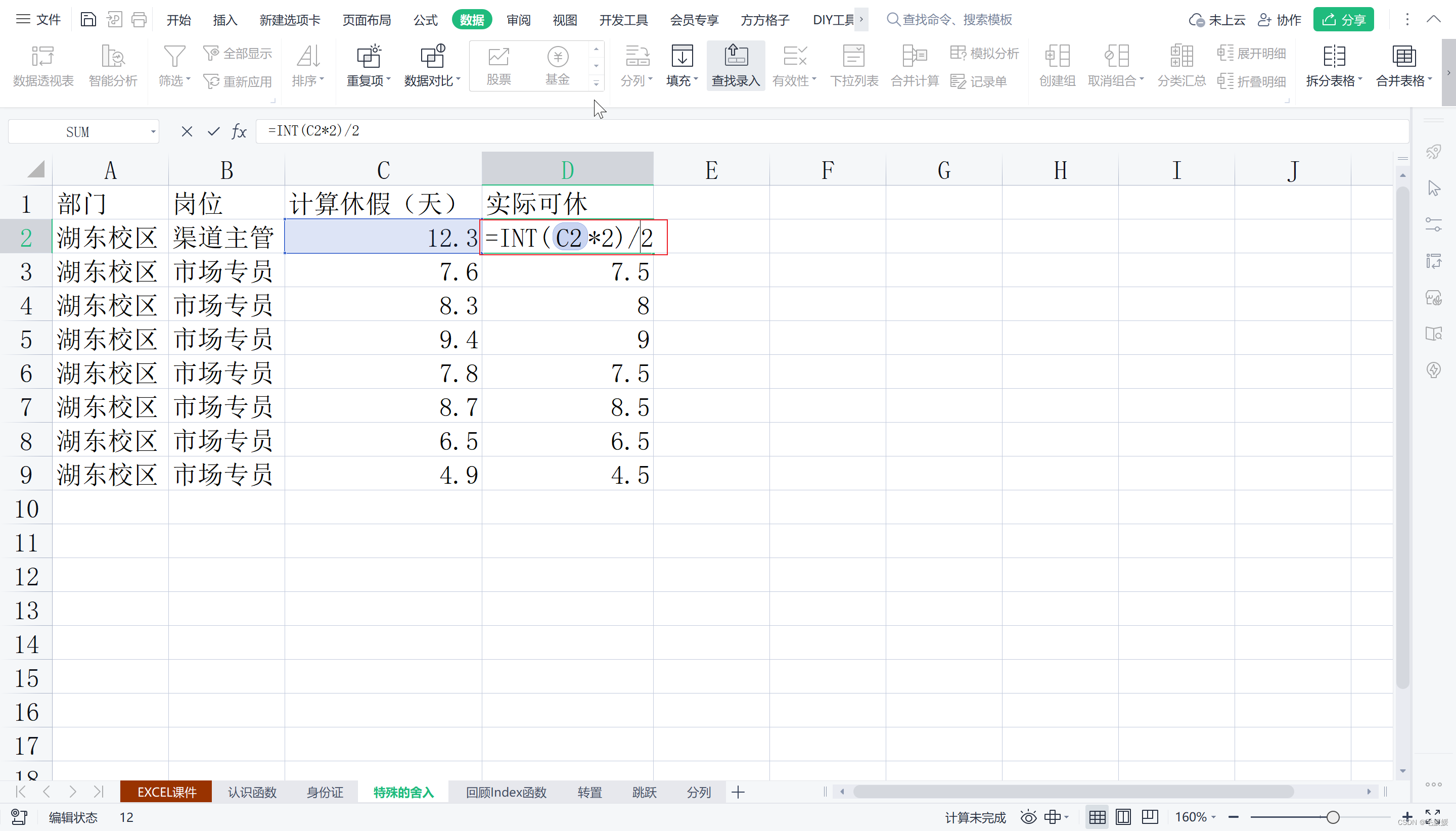
当把一个数据放大2倍再取整，如果小数部分小于0.5，乘2肯定不足1，取整之后会被舍弃；如果小数部分大于等于0.5，乘2肯定会大于或等于1，整数部分会向前进1。

3.基于位置规律的引用

(1) 转置

INDEX(数组,行序数,[列序数],[区域序数])
返回数据清单或数组中的元素值，此元素由行序号和列序号的索引值给定。

• 目标
  
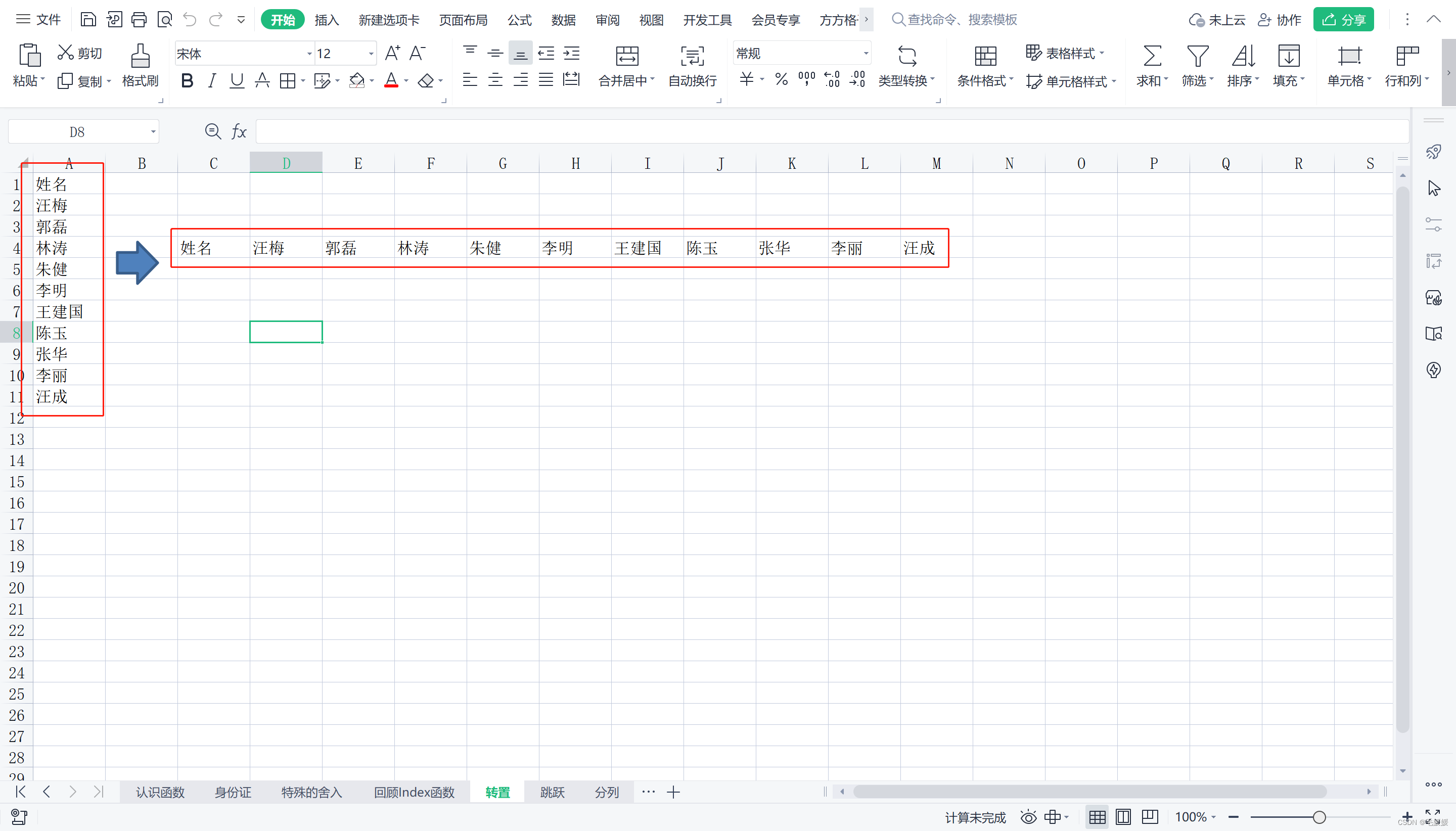
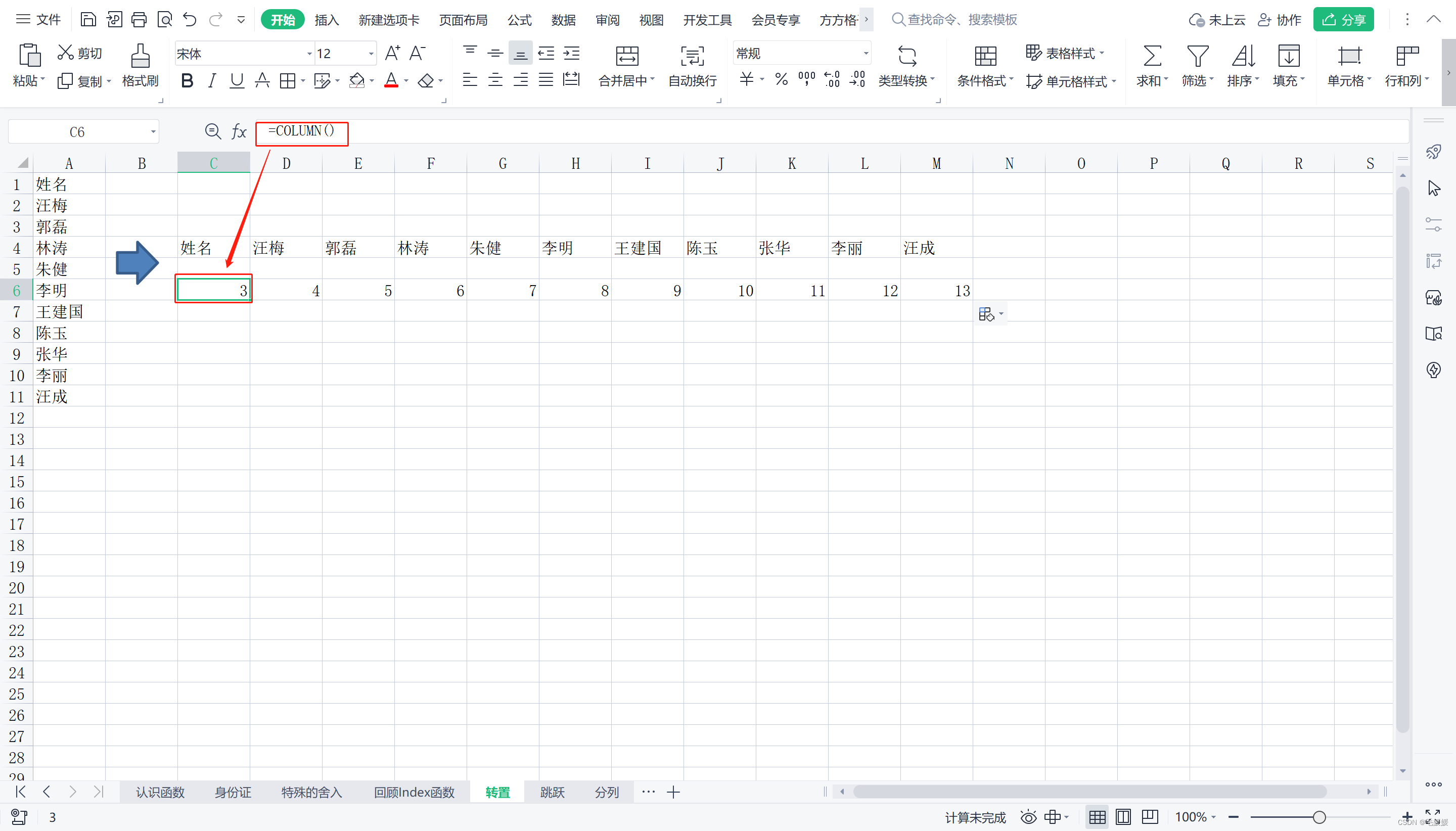
• 步骤
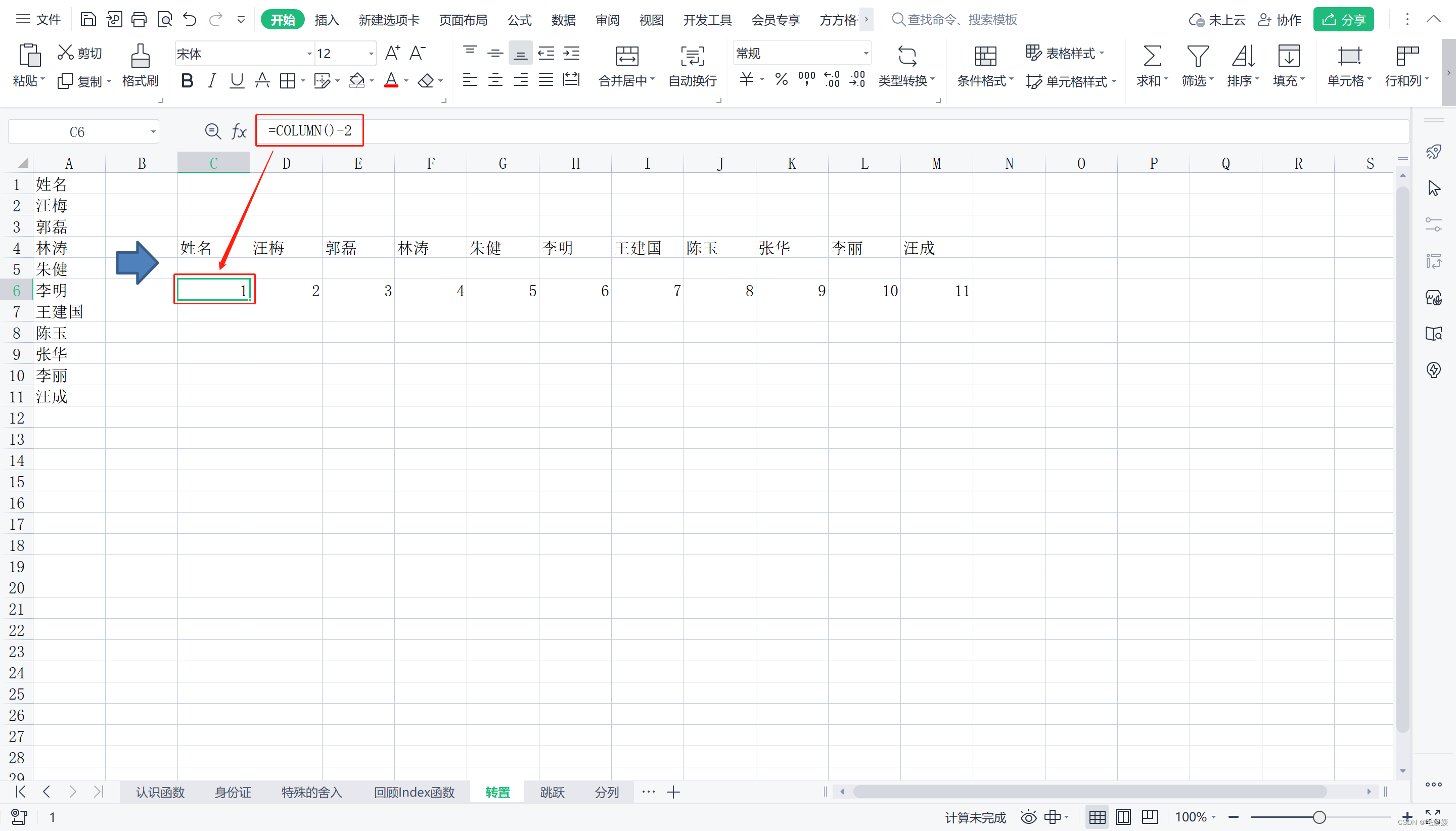
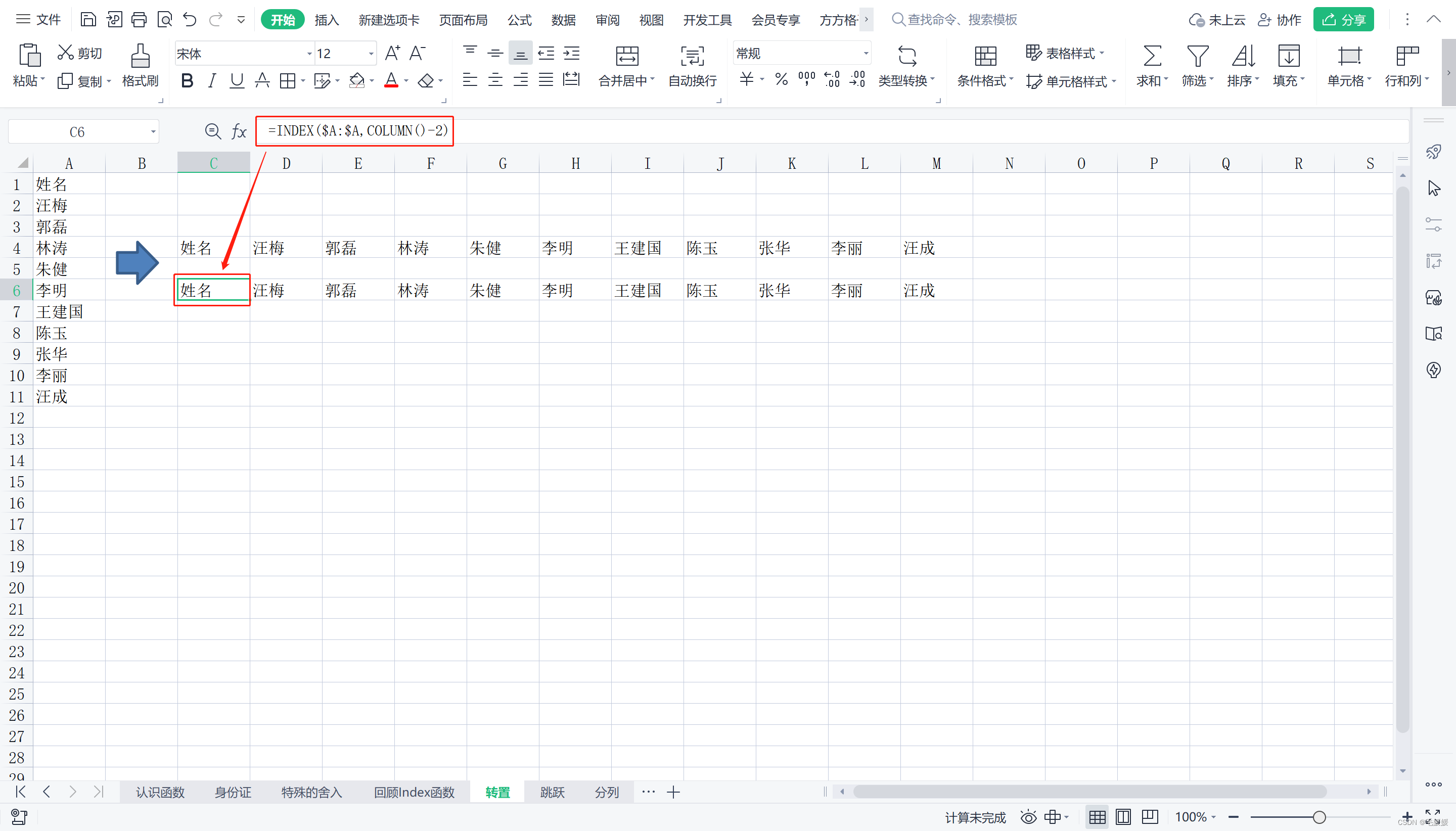
  转置后的数据列序号应当从1开始，向后递增；但利用coulmn()函数计算出来时从3开始的，因此需要减2；然后利用index()函数获取列序数的索引值。
  
  
  
  
  

(2) 跳跃取数

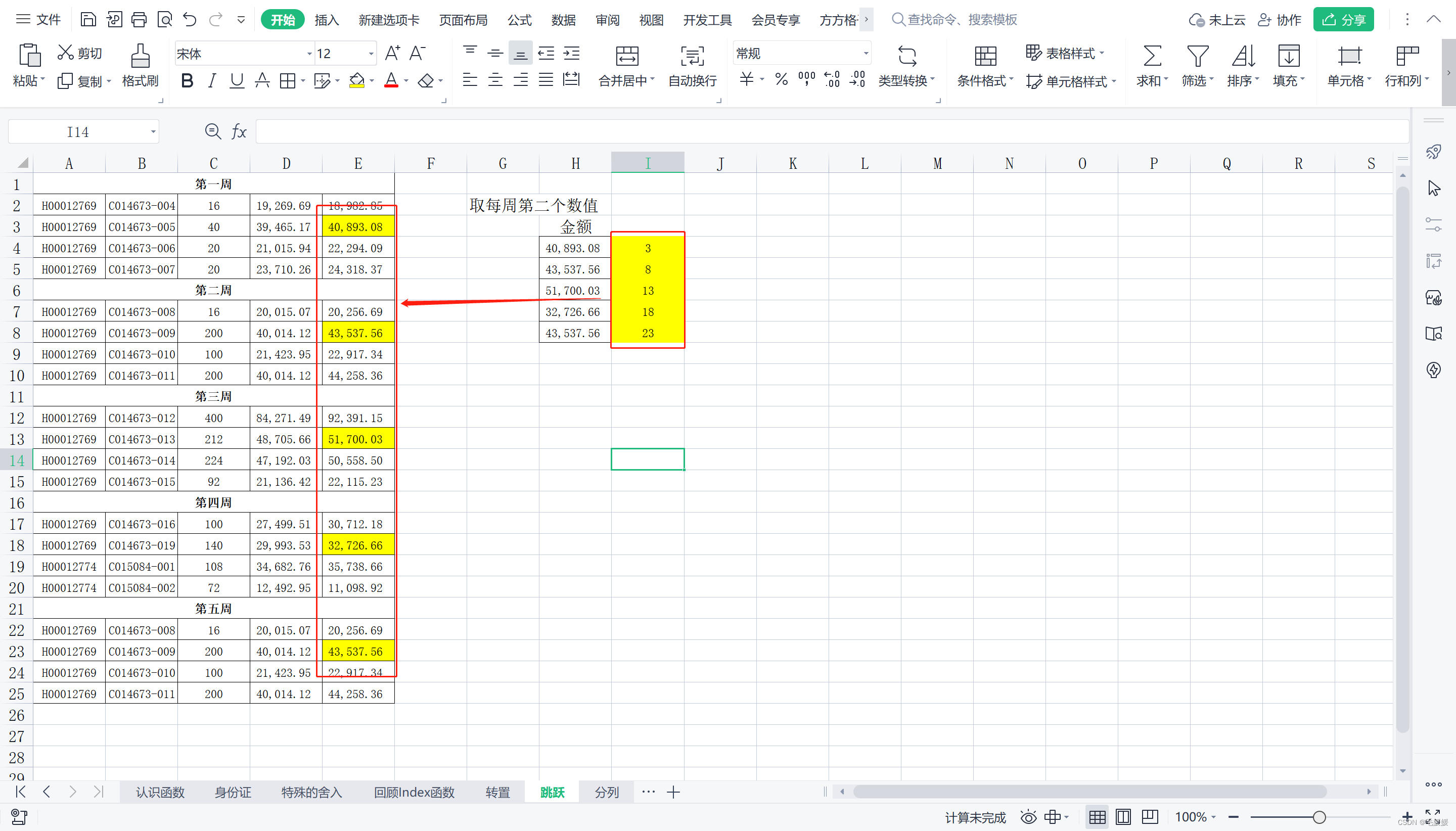
• 取每周第二个数值
  首先，不难发现待取数据都位于一列，所以是用row()计算；又因为对应的行号分别是“3、8、13、18、23”，放大就是做乘法；最后用index()函数获取具体数据。
  
  
  
  
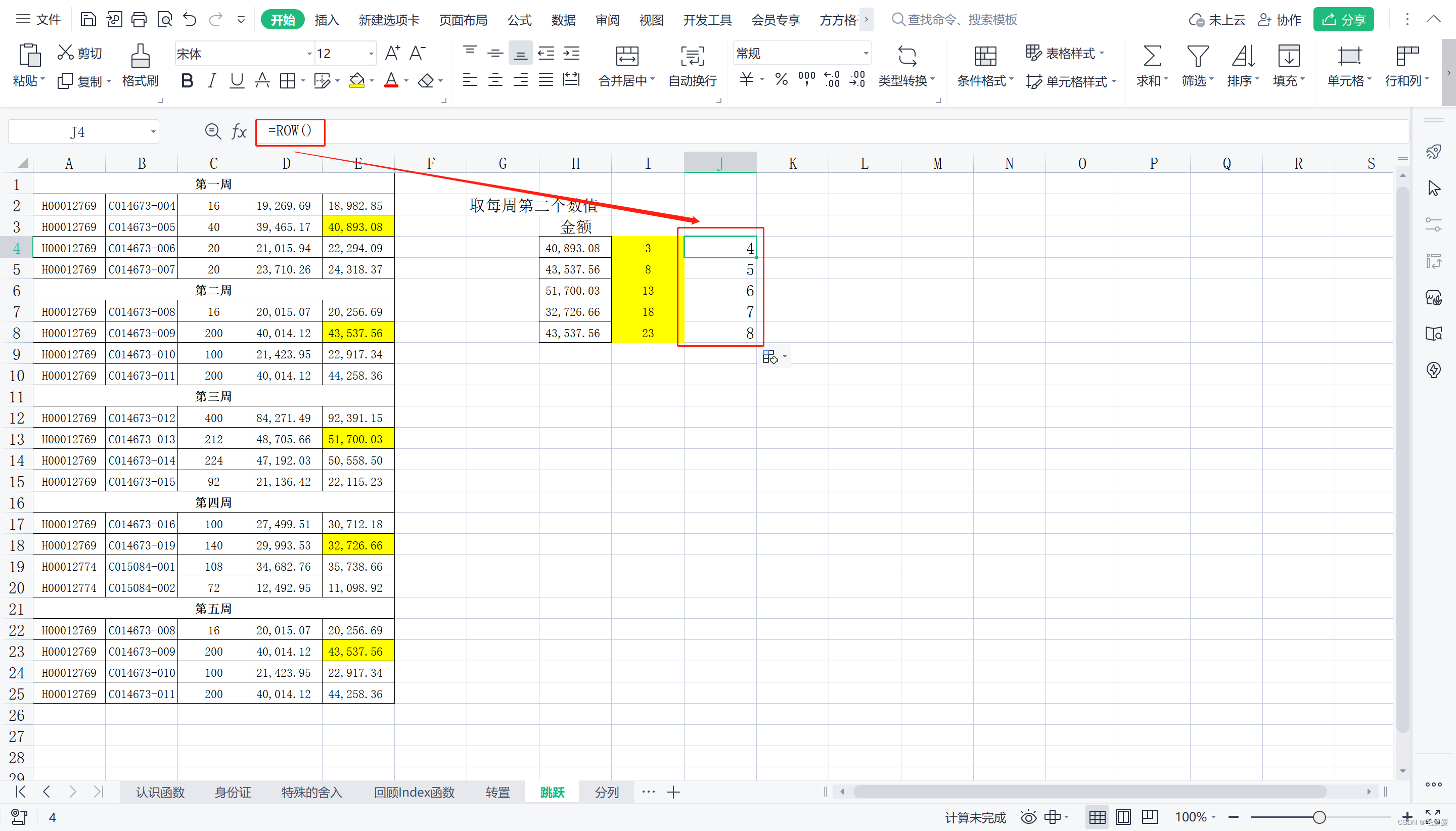
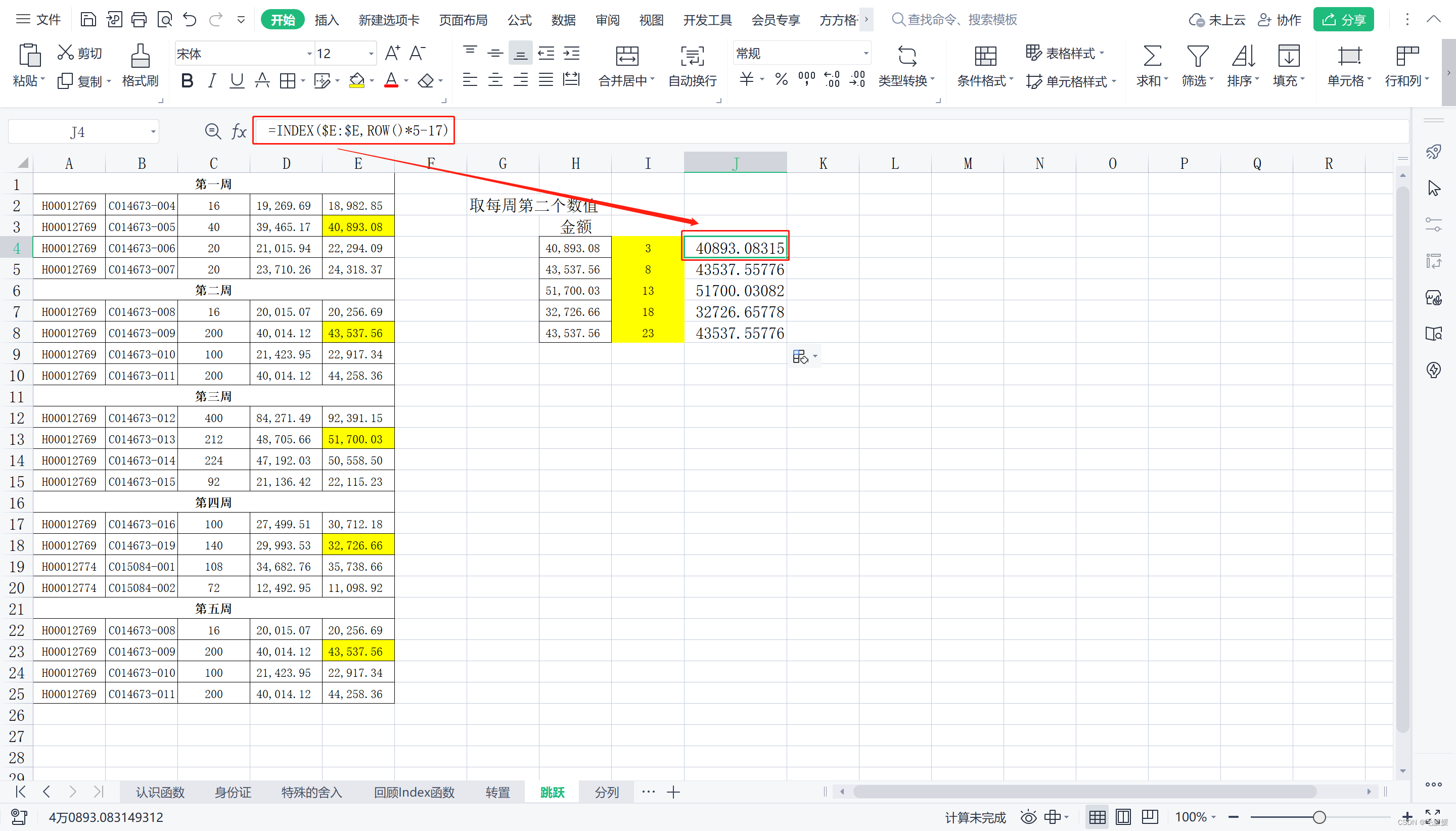
  放大就是乘，缩小就是除，循环就是取余
  
  

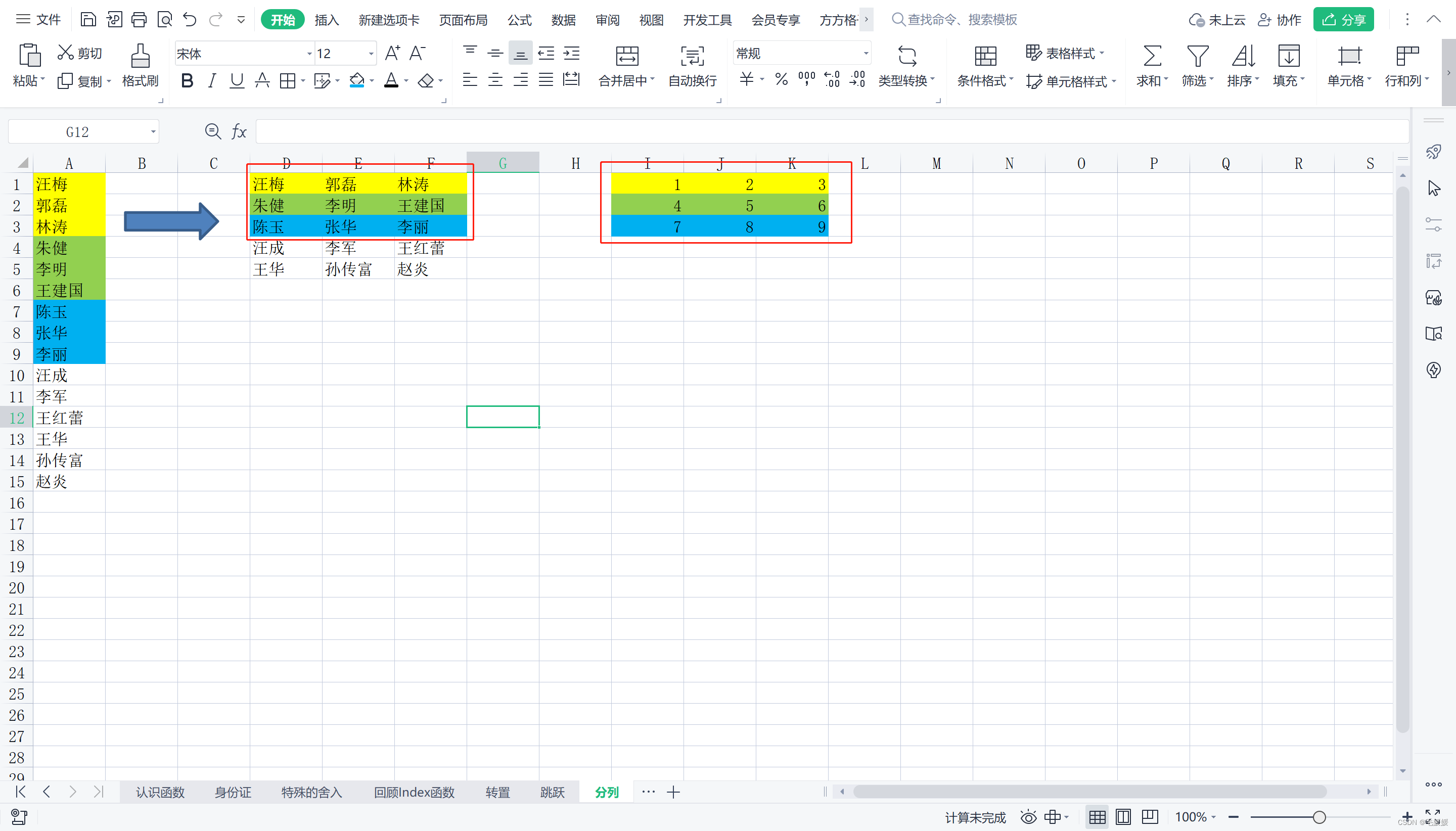
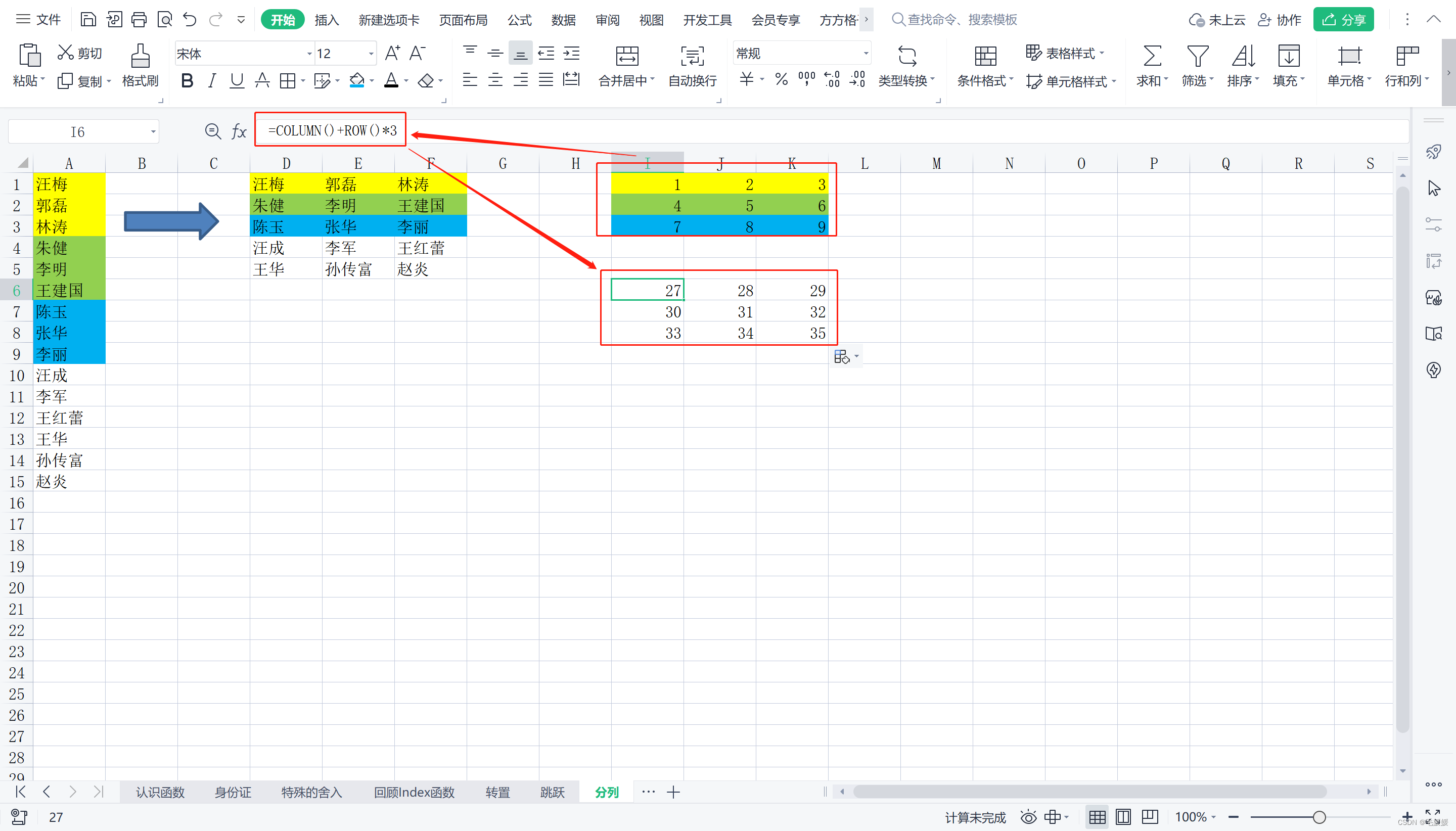
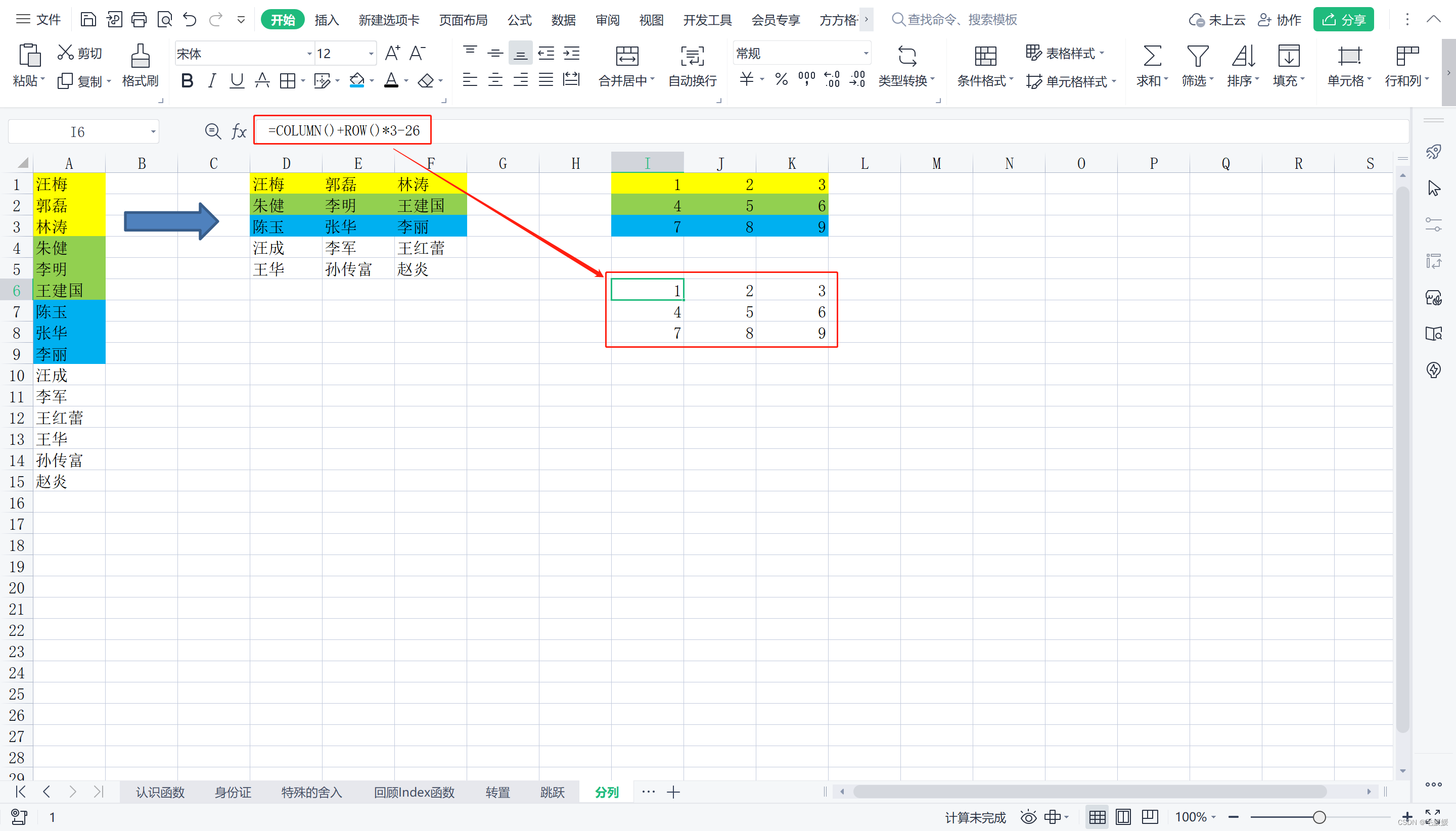
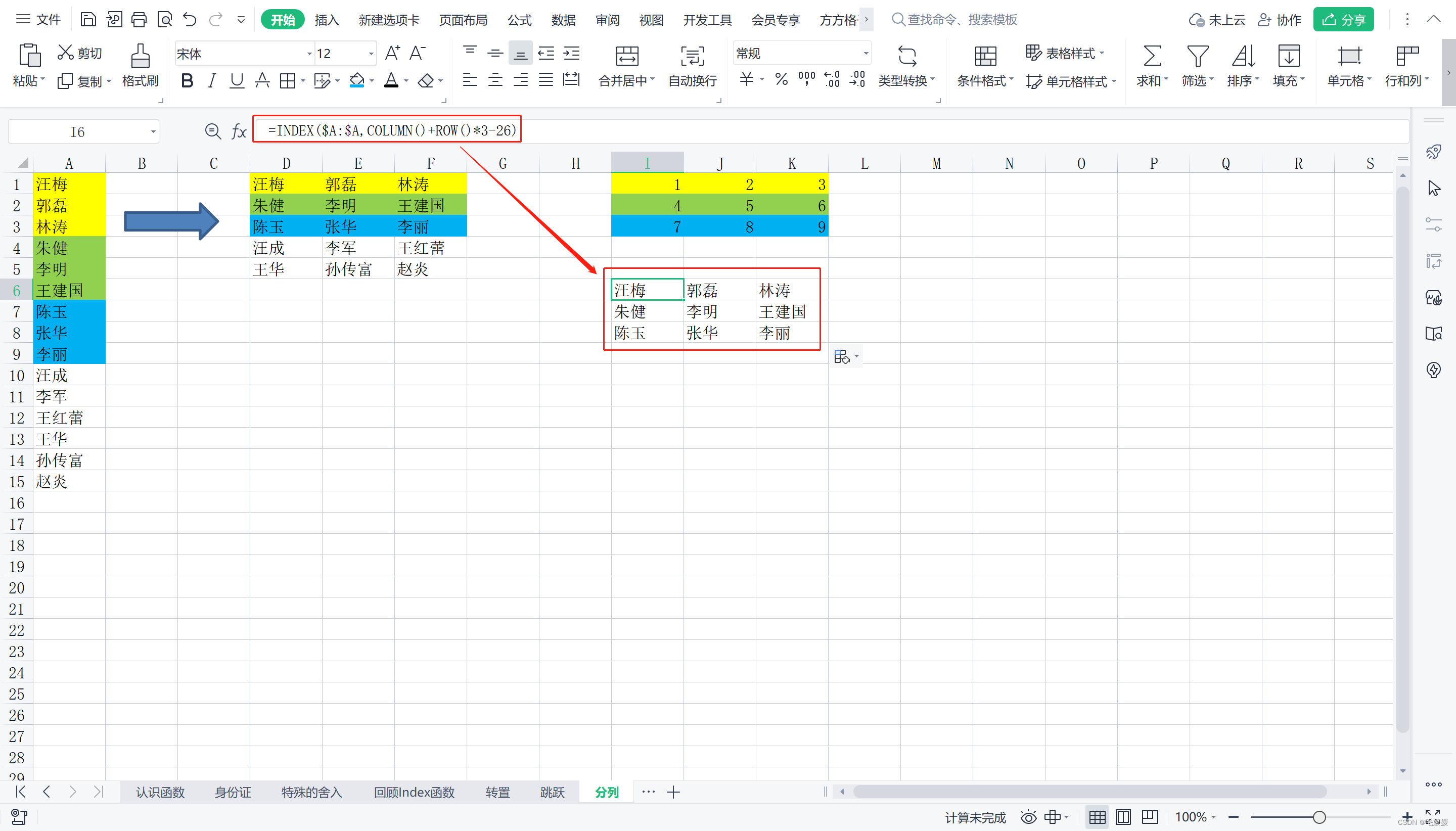
(3) 分列

首先，不难发现待取数据既按照列递增1，又按照行递增3，所以与row()和column()都有关系，且行row()*3，列column()*1；然后调整起点，最后用index()函数获取具体数据。

系列文章目录

第1讲：excel常用的基础操作
第2讲：excel单元格格式设置
第3讲：查找、替换、定位
第4讲：排序与筛选
第5讲：分类汇总、数据有效性
第6讲：数据透视表
第7讲：excel常用函数与公式
第8讲：if函数
第9讲：countif函数
第10讲：sumif函数
第11讲：vlookup函数
第12讲：match+index函数
第14讲：日期函数
第15讲：条件格式与公式
第16讲：简单文本函数
第17讲：数学函数
第18讲：lookup和数组
第19讲：indirect函数
第20讲：图表基础
第21讲：经典excel动态图表实现原理
第22讲：制作甘特图与动态甘特图
第23讲：双坐标柱形图、饼图美化与ppt图表
第24讲：宏表函数