《计算机组成原理》----2.5 乘除法简介

本节书摘来自华章出版社《计算机组成原理》一书中的第2章，第2.5节， 作 者 Computer Organization and Architecture: Themes and Variations［英］艾伦·克莱门茨（Alan Clements）　著，沈　立　王苏峰　肖晓强 译， 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

2.5　乘除法简介

除了加减法，计算机还必须实现乘法和除法。这两个操作比加减法复杂得多，所需的完成时间也长得多（或需要更复杂的硬件）。这里仅介绍乘法和除法的基本知识。

2.5.1　移位运算

在讨论如何进行二进制乘法之前，我们首先介绍二进制补码数的算术移位运算。本节将其简称为“移位”。进行移位运算时，一个数的所有位都会向左或向右移动一位（例如，将二进制数00101100左移一位，它将变为01011000，右移一位将变为00010110）。有些计算机每次可以移动多位。

二进制补码正数左移一位等价于将该数乘2。十进制数39的二进制表示为00100111，左移一位得到01001110，对应于十进制数78。图2-2a描述了算术左移的过程。空出的最低位补0，移出的最高位保存在计算机的进位标志中，进位标志在图2-2中用C表示。进位标志是计算机中的一个位存储单元，保存了进位位的状态。

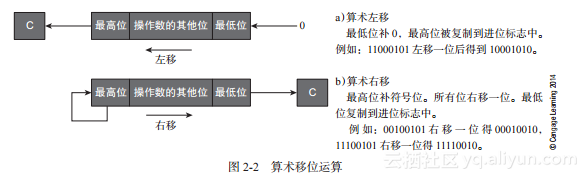
图2-2　算术移位运算
11100011左移一位得到11000110。有符号二进制补码数11100011表示十进制数-29。左移一位之后的结果是11000110，表示十进制数-58。

二进制数右移一位相当于它除以2。以00001100（即1210）为例，右移一位得到00000110（即610）。注意，00001101（即1310）右移一位也会得到00000110，也是610。这是因为移出的最低位被丢弃了。

负数右移需要特别注意。简单地将二进制补码负数11100010右移一位，结果为01110001，这显然是不正确的。为了在移位时保持二进制补码数的符号不变，右移时应该像图2-2(b)那样复制符号位。请考虑11100010（即-30）。右移一位同时保持符号位不变将得到11110001，等价于-15。

为什么通过右移一位实现二进制补码数除以2时要在最高位补符号位？二进制正数定义为0xxxx,…,xx，这里x为1或0。将该数除以2，会得到00pppp,…, pp。这个数的补数为1yyyy,…, yy+1（这里每个y是对应的x的补）。现在把00pppp,…, pp转换为负数，会得到11qqqq,…, qq+1。正如我们所看到的那样，无论是正数还是负数，右移时符号位都应保持不变。

2.5.2　无符号二进制乘法

请回顾人们在纸上笔算两个数乘法的过程。这里之所以强调人们是因为计算机不会像人那样进行乘法运算——它是将所有部分积加到一起。计算机从乘数的最低位开始，每次检查一位，判断它是否为0。如果乘数的当前位为1则写下被乘数，若该位为0则写下n个0。接下来检查乘数的下一位，但这时应从上一个数的左边一位开始写下被乘数（或0）。被写下的这一组数叫作部分积。在得到所有的部分积之后，将它们加到一起，得到乘法的结果。

乘法的结果100000102 = 13010是个8位二进制数。两个n位二进制数相乘会得到一个2n位的积。正如前面提到的那样，数字计算机并没有实现上面的算法，因为这种算法要求计算机存储n个部分积，然后将它们同时相加。一种更好的技术是每得到一个部分积时就做一次加法。图2-3给出了一个计算两个n位无符号二进制数相乘的算法。请考虑用图2-3描述的算法计算1101 × 1010的例子。表2-3给出了其计算过程。

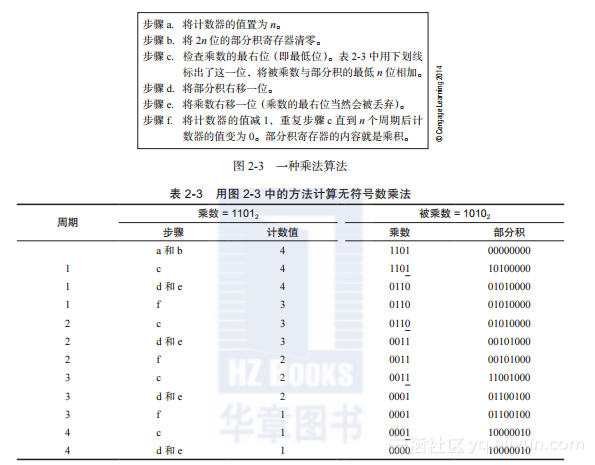
2.5.3　快速乘法

这种通过移位和加法实现的乘法速度很慢。实际的计算机采用了多种方法加快乘法运算的速度。例如，构造专门的逻辑阵列直接得到两个数的积而不必对操作数移位。

有些程序员使用移位和加法等速度相对较快的操作以避免使用乘法。请考虑P乘以10和乘以9这两个例子。

10P = 2×（2×2×P + P）；即将P左移两次，加上P，再将和左移一次。

9P = 2×2×2×P + P；即将P左移三次，加上P得到结果。

乘法运算也可以借助查找表（look-up table）实现，这种方法将两个数相乘所有可能的积都保存在一个只读存储器内。这样，只需简单地用X和Y的值找到表中的对应项就可以得到X和Y的乘积。例如，两个8位二进制数乘法需要一个16位地址（即两个8位字）、216项的查找表，每项记录了一个16位的积。计算00001010乘以00111100的积只需读出地址为0000101000111100的项的内容00000010010110000。

这种方法的缺点在于所需ROM的容量随着乘数和被乘数位数的增加呈指数增长。n位乘法需要的ROM容量为2n×22n位；例如8位乘法需要容量为16×216位的ROM。

可以用一个简单的方法来减少查找表的大小。假设要计算两个16位数A与B的乘积。可以将16位数A拆分为两个8位数Au和Al，这里Au是A的高8位而Al是A的低8位。如果A=1111000010101010，则Au=11110000，Al=10101010。A可被表示为Au×256+Al，B可被表示为Bu×256+Bl。现在，请考虑乘积A×B。

A×B=（Au×256+Al）×（Bu×256+Bl）=65536AuBu+256AuBl+256AlBu+AlBl

这个表达式需要计算4个8位乘积（AuBu，AlBu，AuBl，AlBl），将积左移16位或8位（即乘以65536或256），以及将4个部分积相加等操作。这样，可以用8位乘法和4个加法来完成16位乘法。实际上，借助硬件有很多办法可以加快乘法运算的速度。

2.5.4　除法

除法是通过被除数不断地减去除数直到结果为零或小于除数来实现的。减去除数的次数称作“商（quotient）”，最后一次减法的差称作“余数（remainder）”。也就是说，

被除数/除数 = 商 + 余数/除数

在讨论二进制除法之前，我们首先看看人们在纸上笔算完成十进制除法的过程。下面的算式描述了575除以25的过程。

第一步是比较除数和被除数的最高两位，看看被除数的最高两位中有几个除数。这个例子中答案为2（即2×25 = 50），并用57减去2×25。在商的最高位上写下数字2，得到下面的算式。

将被除数的下一个数字5移下到7的后面，并比较除数和75。由于75正好是25的整倍数，因此应在商的下一位上写下数字3并得到

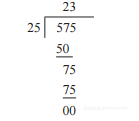
因为已经处理到被除数的最后一位且75正好是除数的整倍数，因此除法结束，商为23，余数为0。上述除法过程的难点在于估计部分被除数中有多少个除数（即57除以25等于2余7）。请考虑用无符号二进制除法完成同样的例子。

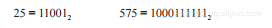
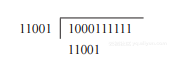
被除数的前5位比除数小，因此商的最高位商0并将除数与被除数的前6位比较。

被除数的前6位中有一个除数，减法后得到新的部分被除数为001010（1111）。将被除数的下一位移下来，可得

新的部分被除数小于除数，因此商的下一位商0。后续的除法过程如下：

除法结果商为10111，余数为0。
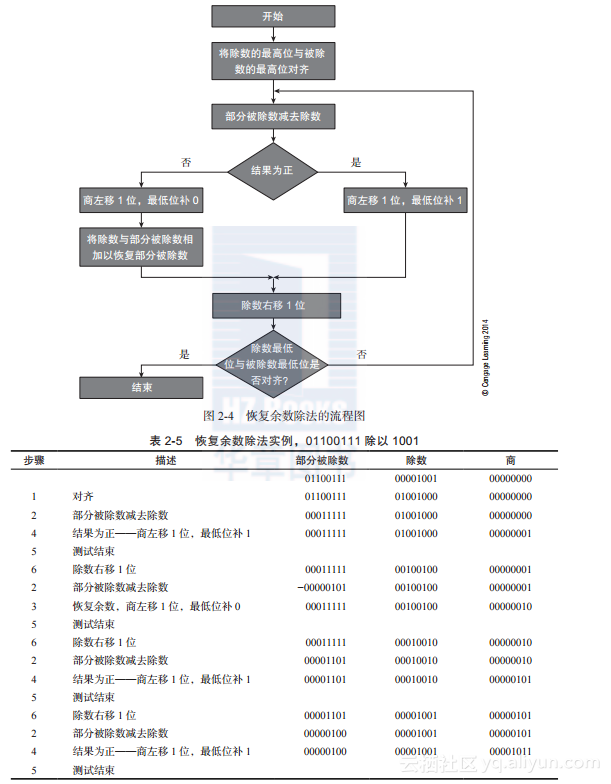
1.恢复余数除法
稍加改动，刚才讨论的除法方法就可以以数字形式实现。唯一需要修改的就是除数与部分被除数的比较方法。人们用心算进行比较，而计算机必须做减法并检测结果的符号位。如果减法的结果为正，则商1，但若结果为负，则应商0并将部分被除数与除数相加，将其恢复为原先的值。

下面是一个可行的恢复余数除法算法。
1）将除数的最高位与被除数的最高位对齐。
2）从部分被除数中减去除数，得到新的部分被除数。
3）若新的部分被除数为负，则商0并用新的部分被除数加上除数，恢复原先的部分被除数。
4）若新的部分被除数为负，则商1。
5）判断除法是否结束。若除数的最低位与部分被除数的最低位对齐，则除法结束。最后的部分被除数就是余数。否则，执行第6步。
6）将除数右移1位。从第2步继续执行。

图2-4描述了该算法的流程图。下面按照该流程计算011001112除以10012，即十进制数103除以9，其结果为商11余4。表2-5逐步列出了除法的过程。

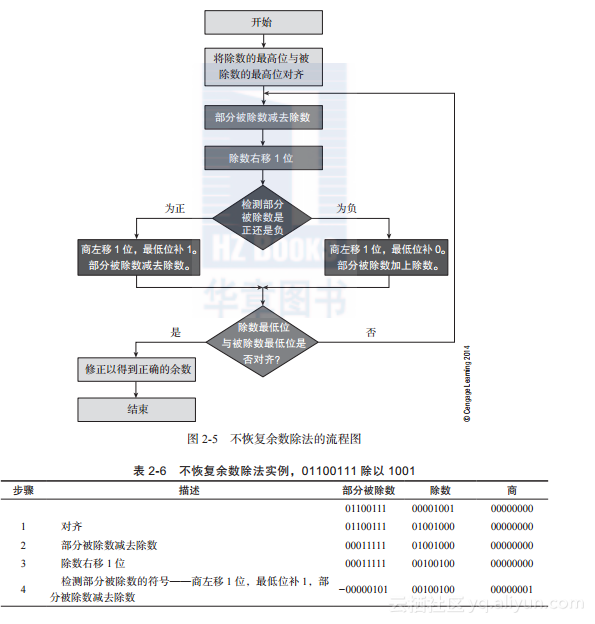
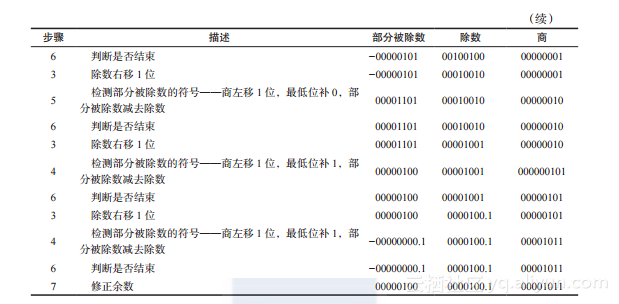
2.不恢复余数除法
改进图2-4中的恢复余数除法可以减少除法的延迟。不恢复余数除法与恢复余数法基本相同，唯一的区别在于它取消了恢复余数的操作。在恢复余数除法中，在部分被除数与除数相加恢复部分被除数之后的一个周期，部分被除数将减去除数的二分之一。每个将除数右移的操作等价于将除数除以2。当前周期恢复部分被除数以及下个周期减去除数一半的操作等价于部分被除数加上除数的一半。即D - D/2 = +D/2，这里D为除数。

图2-5给出了不恢复余数除法的流程图。部分被除数减去除数之后，将检测新的部分被除数的符号位。若为负，则商左移1位，商的最低位补0，并将部分被除数加上除数的二分之一。若为正，则商左移1位，商的最低位补1，并将部分被除数减去除数的二分之一。表2-6列出了用不恢复余数除法完成表2-5中算例的过程。