ALI比GAN的优势在哪里？

本文参考：Adversarially Learned Inference，（2017.2）作者：Vincent Dumoulin（MILA, Université de Montréal,）
原文：https://ishmaelbelghazi.github.io/ALI/

生成模型有三种：（1）VAE，（2）GAN，（3）Autoregressive approaches (这个方法我还没有学习过)。这三种方法皆有优缺点：
1、VAE，image samples from VAE-trained models tend to be blurry，即VAE生成的图像较模糊；
2、GAN，GAN-based approaches represent a good compromise: they learn a generative model that produces higher-quality samples than the best VAE techniques without sacrificing sampling speed and also make use of a latent representation in the generation process. However, GANs lack an efficient inference mechanism, which prevents them from reasoning about data at an abstract level.
3、Autoregressive approaches据文中说是生成效果不错，就是计算量太大，处理得太慢。
ALI（Adversarially Learned Inference，对抗性推断学习）模型的目标是将VAE和GAN联系起来，同时具备速度快、质量好，而且能有效推断。
此处的“有效推断”是什么？就是给定x（数据集样本），产生了什么z（隐变量），即得到以下叙述中的概率分布 $q(\mathbf z \vert \mathbf x)$。GAN是由z产生x，它不管给定x产生什么z，没有从x到z的推断过程。现在ALI采用了VAE的编码器和解码器结构，于是便具有了此项推断功能，同时，它的训练过程与传统VAE不同，采用的是GAN那样的纳什均衡方式的训练方法，因此说：ALI具有VAE的实现架构，又有GAN的训练方法。实现框架提供了推断方法，训练方法提供了高质量的生成过程。具体如图1：

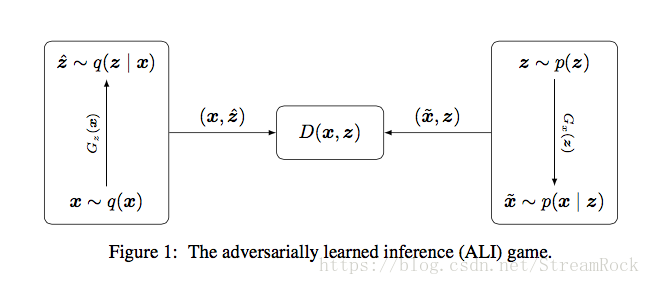
图1 ALI模型

• 图1中左边为Encoder：样本 $\mathbf x$ 从经验分布 $q(\mathbf x)$ 抽样出来，经过Encoder的映射
  $G_z(\mathbf x)$ 得到条件分布 $q(\mathbf z \vert \mathbf x)$，从中抽样出 $\hat {\mathbf z}$，由此形成一个联合分布$q(\mathbf x, \hat {\mathbf z})$，有 $q(\mathbf x, \hat {\mathbf z}) = q(\mathbf x)q(\mathbf {\hat z} \vert \mathbf x)$；
• 图1右边为Decoder：已知一个分布 $\mathbf z \sim p(\mathbf z)$，例如：$p(\mathbf z)=N(\mathbf 0, \mathbf I)$ 标准正态分布。从该分布中抽样出一个样本$\mathbf z$，经过Decoder映射$G_x(\mathbf z)$得到一个条件分布$p(\mathbf x \vert \mathbf z)$，从该分布抽样出 $\hat {\mathbf x}$，于是形成一个联合分布 $p(\hat {\mathbf x}, \mathbf z)$，有 $p(\mathbf {\hat x}, \mathbf z) = p(\mathbf z)p(\mathbf {\hat x} \vert \mathbf z)$；
• 图1中间是一个判别器，它的判别函数为 $D(\mathbf x, \mathbf z)$，它的作用是：分辨输入的联合分布样本来自 $q(\mathbf x, \hat {\mathbf z})$ ，还是来自 $p(\hat {\mathbf x}, \mathbf z)$。

具体的实现可以由以下伪代码来说明：

我们从实现的过程来看，ALI虽然也有Encoder和Decoder，但它们却是独立工作的，这与VAE有着巨大的差别：
1、VAE原理

$$\require{AMScd} \begin{CD}\mathbf x @>\text{Encoder map}>> p(\mathbf z \vert \mathbf x)\\@| \Vert \mathbf x-\mathbf {\hat x} \Vert @VV\text{sample}V\\\hat{\mathbf x} @<\text{Decoder map}<< \hat{\mathbf z} \end{CD}$$
VAE的 $\mathbf x$ 和 $\mathbf {\hat x}$ 是有关系的： $\mathbf x$ 经Encoder map得到条件分布 $p(\mathbf z \vert \mathbf x)$，经抽样得到 $\mathbf {\hat z}$，然后再经过Decoder map得到重建 $\mathbf {\hat x}$，Loss与原样本与重建样本的距离有关： $Loss\sim \Vert \mathbf x-\mathbf {\hat x} \Vert$。
2、ALI 的Encoder与Decoder是独立工作的，它们各自生成联合分布，交由判别器判定是否相同分布，期间映射和采样都是独立进行的，这一点从它的Loss构造中可见一斑。ALI的价值函数（Value Function）是直接从GAN中继承过来的：

• 一般的GAN价值函数：
  

  $$\min_{G} \max_{D} V(D,G)= \mathbf E_{q(\mathbf x)}[\log D(\mathbf x)]\ + \ \mathbf E_{p(\mathbf z)}[1-\log (D(G(\mathbf z)))] \\ = \int q(\mathbf x) \log D(\mathbf x) d\mathbf x + \iint p(\mathbf z)p(\mathbf x \vert \mathbf z)[1-\log D(\mathbf x)]d\mathbf x d\mathbf z\qquad(1)$$

• ALI 的价值函数是将(1)中 $D(\cdot)$ 的边沿分布替换成联合分布，有：
  

  $$\min_{G} \max_{D} V(D,G)= \mathbf E_{q(\mathbf x)}[\log D(\mathbf x, G_{\mathbf z}(\mathbf x))]\ + \ \mathbf E_{p(\mathbf z)}[1-\log (D(G_{\mathbf x}(\mathbf z), \mathbf z))] \\ = \iint q(\mathbf x)q(\mathbf z \vert \mathbf x) \log D(\mathbf x, \mathbf z) d\mathbf x d \mathbf z+ \iint p(\mathbf z)p(\mathbf x \vert \mathbf z)[1-\log D(\mathbf x, \mathbf z)]d\mathbf x d\mathbf z\qquad(2)$$
  匹配了 $q(\mathbf x, \mathbf z)$ 和 $p(\mathbf x, \mathbf z)$，就意味着匹配了一系列边沿分布和条件分布：
  $$q(\mathbf x)\sim p(\mathbf x) \quad q(\mathbf z)=p(\mathbf z) \\ q(\mathbf x \vert \mathbf z)\sim p(\mathbf x \vert \mathbf z) \quad q(\mathbf z \vert \mathbf x)\sim p(\mathbf z \vert \mathbf x)$$
  由上述关系可以完成相应的推断。

ALI的性能可以由下面一个简单实验来说明：

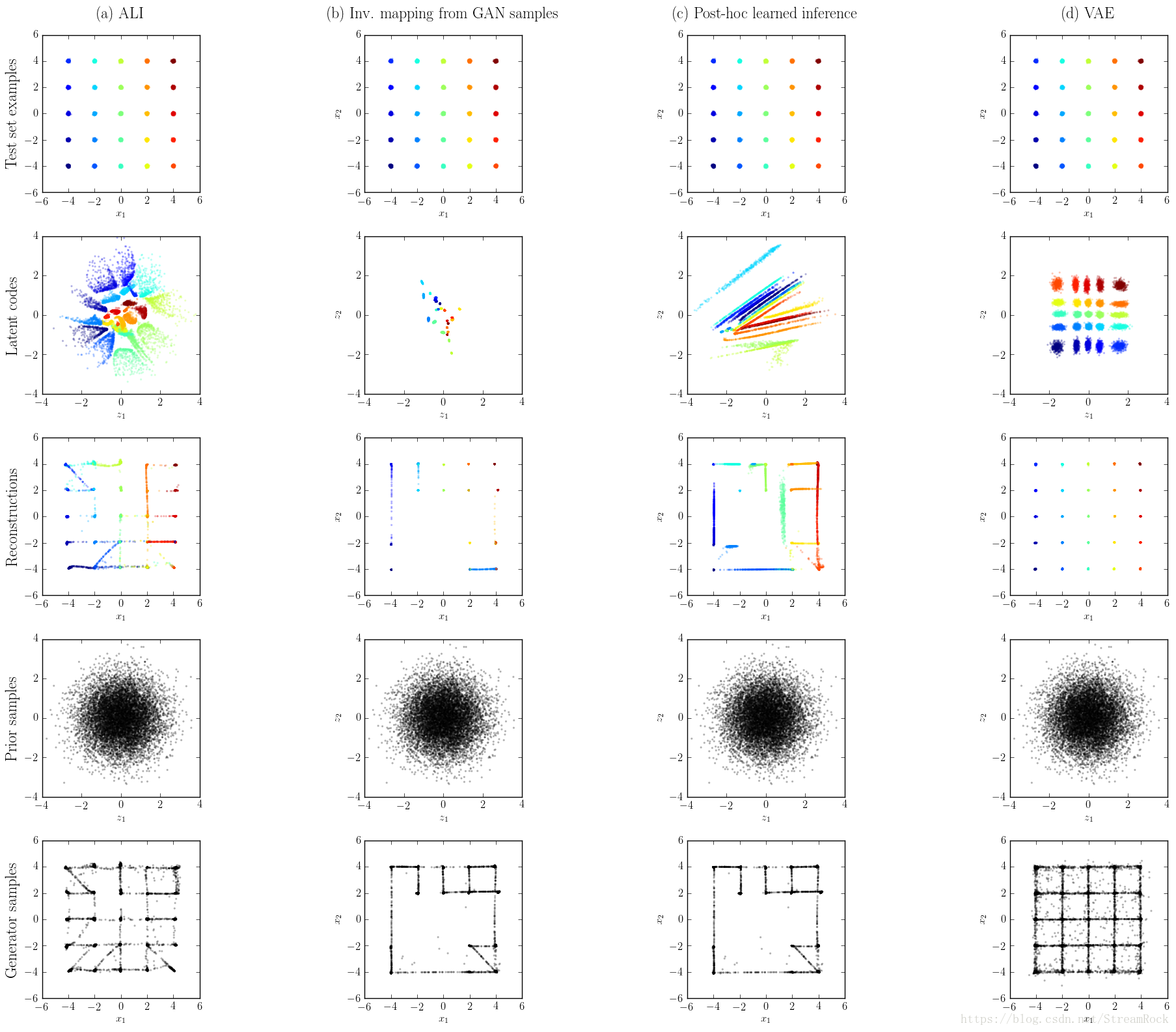
图2 各模型效果对比图
这是一个Toy dataset实验：经验分布是一个2D分布，其密度函数 $q(\mathbf x)$ 由25个2D高斯混合分布合成，如图中第一行。第二行是给定$\mathbf x$ 生成的隐变量 $\mathbf z$ 的分布，它也是2D的。第三行是由隐变量重建样本，第四行是$\mathbf z$ 的先验分布：$\mathbf z \sim N(\mathbf 0,\mathbf I)$ ，第5行是直接先验分布得到$\mathbf z$，并由此生成的重构样本。
由图2，GAN生成的样本模式最少，因而很容易进入模式坍塌；而VAE和ALI生成样本多样性的效果较好；VAE点与点之间的连线明显，这从一个侧面反映出VAE生成图像会较模糊；ALI既能生成多样性样本，点与点之间连线不如VAE明显，是一种较好的方案。
笔者经验：ALI的训练很困难，收敛太慢了。