[学习笔记]NOIp2017小凯的疑惑及其推广

本文主要是介绍[学习笔记]NOIp2017小凯的疑惑及其推广，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

小凯的疑惑题面
两个数a,b，求最大的不能被a、b表示的数
2017年我没参加提高组，所以没有体会到此题毒瘤程度，据说一堆大佬死在了这题上面
首先，结论题，猜结论十分简单： $a * b - a - b$
那么怎么推出来呢
以样例3、7为例
建立一个n*7的矩阵
在这里插入图片描述
红色部分都是能表示的，显然，答案是11（最大的白色的数）
我们可以发现矩阵中的某些性质

上下相邻的两个数相差7
每一列中第一个红色的数一定是第一个被3整除的数（除了最后一列）

因为上下相邻的两数相差7，所以一列中只要其中一个能被表示出来，那么正下方的数就一定可以被表示出来
那么一列中最小的能被表示出来的数一定是3k（最后一列不讨论，因为最后一列是7的倍数）

然后发现11下方18刚好是几列中最大的最小的能被表示出来的数
再来看一组好的数据：4、7
建立一个4*7的矩阵
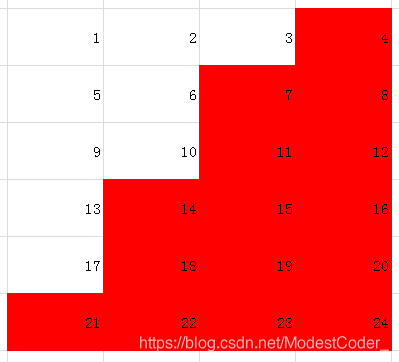
在这里插入图片描述
发现规律了没？
$21 = 3 * 7 = (4 - 1) * 7$
$17 = 21 - 4 = (4 - 1) * 7 - 4 = 4 * 7 - 4 - 7$
感性理解一下就行了
题目样例也是如此，公式就这么推出来了（看图理解更便捷，我口头论述不清）
代码就不放了~~

----------------------------------------------------------------------

接下来是升级版
在这里插入图片描述
首先这道题可以非常容易得拿到30分小凯的疑惑结论输出；以及40分暴力完全背包，就不加阐述了
想想满分的怎么打

对上面的图加深理解

在这里插入图片描述
发现每一列分别对4取模为1、2、3、0
像一个说法来描述每一列中最小的那个能被表示出来的数
比如21是%4=1的数中最小的能被7表示出来的数
14是%4=2的数中最小的能被7表示出来的数，以此类推
然后，每一列中最大的不能被7表示出来的数是：最小的能被7表示出来的数-4
然后答案是对每一列中最大的不能被7表示出来的数再取个max
也就是 $m a x (每一列中最小的能被 7 表示出来的数 - 4)$

若输入a,b（不妨令a<b），则答案为： $m a x (每一列中最小的能被 b 表示出来的数 - a)$

若输入三个数呢，设输入a,b,c(不妨令a<b<c)
是不是像上面一样建立一个n*a的矩阵，然后每一列中用b,c去表示数，
答案就是 $m a x (每一列中最小的能被 b ， c 表示出来的数 - a)$

那么有n个数的话一样也可以搞

那么看看这道强化题，发现x1<=1e6，说明列数<=1e6
令dis[u]表示最小的能被x2,x3……xn表示的%x1=u的数
dis数组可以跑最短路求得（x1<=1e6，没毛病）
然后答案是max(dis[i]-x1)

是不是很简单？
在这里放个官方题解，不过及其省略

在这里插入图片描述

很明显，题解把怎么做说的清清楚楚，但是为什么并没有解释，所以我就是来解释一下为什么~~
我最短路用了堆优dijk，比spfa稳定

Code：

#include <bits/stdc++.h>
#define maxn 1000010
#define LL long long
using namespace std;
const LL inf = 9999999999999999;
struct node{int num;LL len;bool operator < (const node &x) const{return len > x.len;}
};
priority_queue <node> q;
int n, p, vis[maxn];
LL dis[maxn], a[maxn];inline LL read(){LL s = 0, w = 1;char c = getchar();for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);return s * w;
}int main(){freopen("sequence.in", "r", stdin);freopen("sequence.out", "w", stdout);n = read();if (n == 2){//n=2,小凯的疑惑特判，因为这个情况x1<=1e9，无法最短路LL x = read(), y = read();printf("%lld\n", x * y - x - y);fclose(stdin); fclose(stdout);return 0;}p = read();for (int i = 1; i < n; ++i) a[i] = read();q.push((node) {0, 0});for (int i = 1; i < p; ++i) dis[i] = inf;while (!q.empty()){//最短路过程node tmp = q.top(); q.pop();if (vis[tmp.num]) continue;vis[tmp.num] = 1;for (int i = 1; i < p; ++i){LL u = (tmp.num + a[i]) % p;if (dis[u] > tmp.len + a[i]){dis[u] = tmp.len + a[i];q.push((node) { u, dis[u] });}}}LL ans = 0;for (int i = 1; i < p; ++i) ans = max(ans, dis[i] - p);//求得答案printf("%lld\n", ans);fclose(stdin); fclose(stdout);return 0;
}