本文主要是介绍瞬态响应分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本篇文章介绍当输入为时域输入时获得系统响应的MATLAB方法,这些时域输入可以是阶跃 函数、冲激函数或斜坡函数。同时作出推广,讨论系统对初始条件和任意时间函数的响应。
目录
阶跃响应
标准二阶系统的MATLAB描述
阶跃响应
线性系统的MATLAB表达式
冲激响应
冲激函数
获得冲激响应的另一种方法
斜坡响应
在状态空间中定义的系统的单位斜坡响应。
对任意输入的响应
获得对任意输入的响应。
对任意初始条件的响应
拉普拉斯变换方法
对初始条件的响应(状态空间方法,第一种情况)。
对初始条件的响应(状态空间方法,第二种情况)。
采用命令initial求对初始条件的响应。
阶跃响应
标准二阶系统的MATLAB描述
如下形式的二阶系统
称为标准二阶系统。给定和
后,命令
printsys(num,den)或者 printsys(num,den,'s')
会将num/den显示成s的多项式。
使用ord2命令来能够生成二阶系统,但分子部分没有常数的平方,形如:
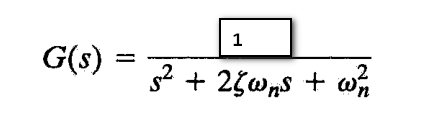
举例来说,现在考虑% = 5 rad/s和,=0.4的情况。
>> wn = 5;
>> damping_ratio = 0.4;
>> [num0,den] = ord2(wn,damping_ratio)
num0 =1
den =1 4 25
>> num = 5^2*(num0)
num =25
>> printsys(num,den,'x')
num/den = 25--------------x^2 + 4 x + 25
阶跃响应
如果已知num和den(传递函数的分子和分母),就可以用
sys = tf(num,den)
来定义该系统。然后,采用
step(sys)或者 step(num,den)
这类命令来产生单位阶跃响应的图形,并在屏幕上显示一条响应曲线。计算的时间间隔和响应时间的长度由MATLAB确定。
如果希望MATLAB每隔秒计算一次响应值,而且画出0 WtWT的响应曲线(其中7'是 At的整数倍),就可以在程序中输入语句
t = 0::T;
然后采用命令
step(sys,t)或 step(num,den,t)
其中的t就是用户指定的时间。
如果step命令具有左端参数,例如
y = step(sys,t)或者 y = step(num,den,t)
和
[y,t] = step(sys,t)或者[y,t] = step(num,den,t)
那么MATLAB会产生该系统的阶跃响应,但是不在屏幕上显示图形。为了观察响应曲线,必 须再采用plot命令。
>> num=25num =25>> den=[1 4 25]den =1 4 25>> sys = tf(num,den)sys =25--------------s^2 + 4 s + 25Continuous-time transfer function.>> step(sys)执行>> step(sys)后,会显示图像。
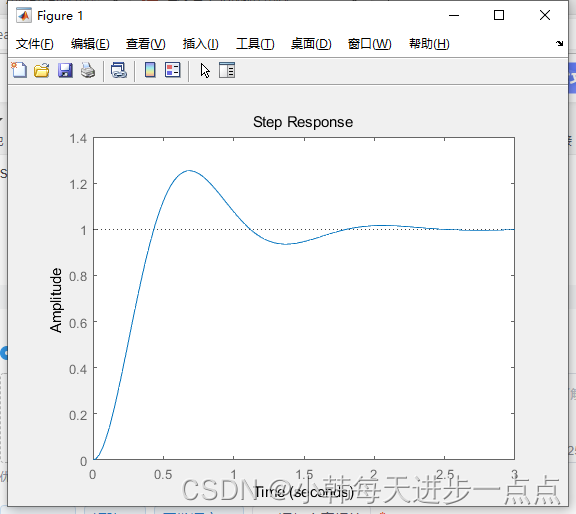
定义时间间隔:
>> t=0:0.1:2;
>> step(sys,t) 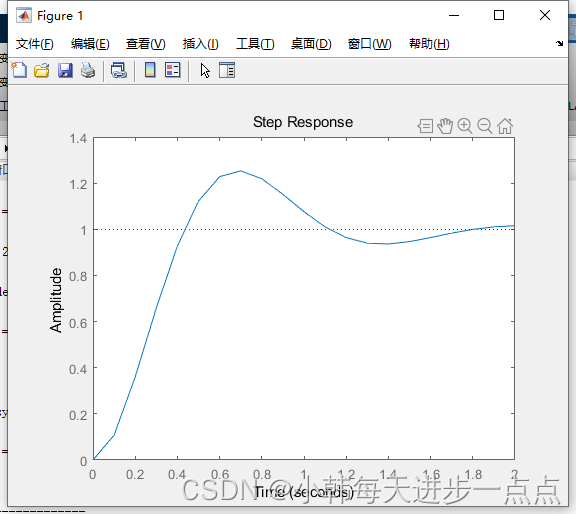
发现曲线是不光滑的,说明MATLAB每隔后计算一次响应值。
需要求得输出值时:
>> [y,t] = step(sys,t)y =00.10770.35990.65820.92711.12211.22811.25321.21891.15171.07611.01000.96370.94000.93620.94650.96430.98330.99951.01041.0156t =00.10000.20000.30000.40000.50000.60000.70000.80000.90001.00001.10001.20001.30001.40001.50001.60001.70001.80001.90002.0000>> plot(t,y)线性系统的MATLAB表达式
当二阶系统不是标准二阶系统时,系统的传递函数采用两个数组表示即可。
对于以状态空间形式定义的控制系统,如果已知状态方程的状态矩阵A、控制矩阵B、输 出矩阵C和直接传输矩阵D,那么
step(A,B,C,D)
会产生单位阶跃响应的图形。当step命令中没有明确包含t时,时间向量会自动确定。 值的注意的是,命令step(sys)可用来获得系统的单位阶跃响应。首先要通过 sys = tf(num,den)或者
sys = ss(A,B,C,D) 来定义系统。然后,为了获得单位阶跃响应,可以输入 step(sys)
当step命令具有左端参数时,例如
[y,x,t] = step(num,den,t)
[y,x,t] = step(A,B,C,D,iu)
[y,x,t] = step(A,B,C,D,iu,t)
这时屏幕上不会显示图形。所以,必须还要采用某个绘图命令来观察响应曲线。矩阵y和x 分别包含在计算时间点t求得的系统输出和状态响应(y的列数和输出数目相同,t中的每个元 素对应y的一行;X的列数和状态数目相同,t中的每个元素对应X的一行)。
其中x,y指的是系统
中的x,y。
回顾一下:
状态空间到传递函数的变换。
为了从状态空间方程获得传递函数,可以采用命令[num,den] = ss2tf(A,B,C,D,iu)
对于输入量多于1个的系统必须指定iu。例如,如果该系统具有3个输入(“u1, u2,u3),那么 iu必须是1,2或3,其中1表示u1, 2表示u2, 3表示u3。
冲激响应
冲激函数
冲激输入。当机械系统在很短的时间内受到很大的力时,例如当弹簧-质量-阻尼器系统 被榔头或子弹打击时,可以观察到系统的冲激响应。从数学意义上讲,这种冲激输入可以表示 为冲激函数。
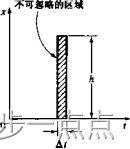
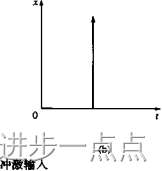
冲激函数是没有任何实际物理对应物的数学函数。但是,如图3.28(a)所示,如果实际输 入持续很短的时间(A,秒),但具有很大幅值(方),以至于时间图形中的区域。Af)不可忽略, 就可以用冲激函数来近似。如图3.28(b)所示,冲激函数通常用一个垂直箭头来表示它具有 很短的持续时间和很大的高度。
在处理冲激函数时,重要的只是函数的幅值(或区域),它的实际形状并不重要。换句话 说,幅值为2奴持续时间为At/2的冲激函数被认为和幅值为奴持续时间为At的冲激函数相 同,只要也趋于是有限值即可。
控制系统的单位冲激响应可以采用下述MATLAB命令中的一条命令来求取:
impulse(num,den)或 impulse(sys)
impulse(A,B,C,D)
impulse(num,den,t)或 impulse(sys,t)
y = impulse(num,den) 或 y = impulse(sys)
[y,t] = impulse(num,den,t) 或 [y,t] = impulse(sys,t)
[y,x,t] = impulse(num,den)
[y,x,t] = impulse(num,den,t)
[y,x,t] = impulse(A,B,C,D)
[y,x,t] = impulse(A,B,C,D,iu)
[y,x,t] = impulse(A,B,C,D,iu,t)
其具体用法用前面提到的阶跃函数具体用法一样.
求如下系统的单位冲激响应:
>> num = [1];
>> den = [1 0.2 1];
>> impulse(num,den);
>> grid
>> title('Unit-lmpulse Response of G(s) = 1/(s^2 + 0.2s + 1)')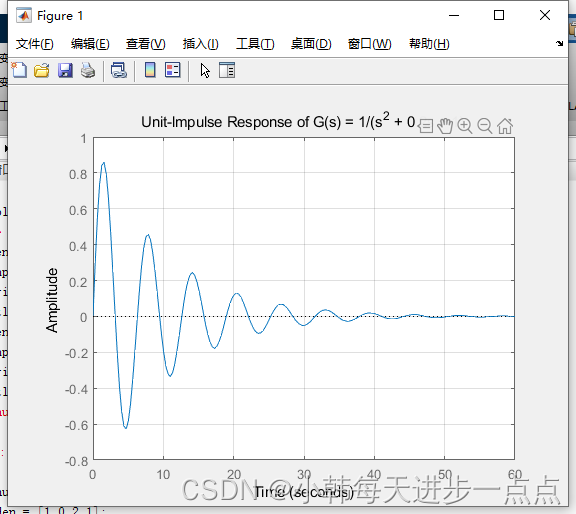
获得冲激响应的另一种方法
我们知道,当初始条件为0时,G(s)的单位冲激响应与sG(s)的 单位阶跃响应相同。s为微分因子。
对单位冲激输入而言,由于R(s) =1,所以有
于是,可以将G(s)的单位冲激响应转化为sG(s)的单位阶跃响应。
>> num = [1 0];
>> den = [1 0.2 1];
>> impulse(num,den)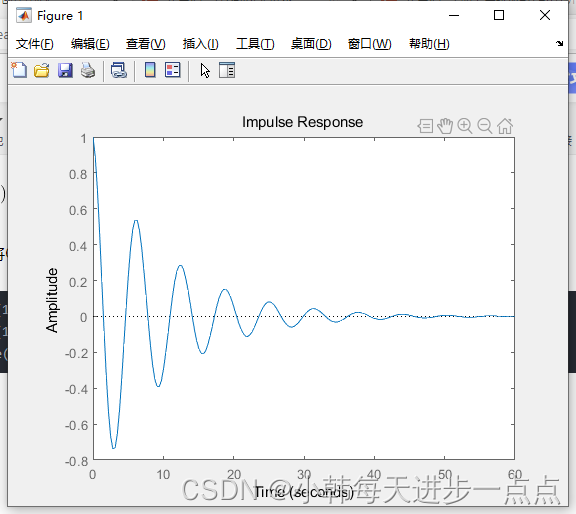
采用阶跃函数命令求系统的冲激响应
>> num=[1 0];
>> den=[1 0.2 1];
>> step(num,den);
>> grid
>> title('Unit-step Response of sG(s)=s/(s^2+0.2s+1)')
>> 
显然,这两种方式求得的图像是相同的。
斜坡响应
在MATLAB中没有关于斜坡响应的命令。所以必须采用step命令或Isim命令(见下文) 来获得斜坡响应。具体地讲,要得到传递函数系统G(s)在零初始条件下的斜坡响应,可以将 G(s)除以s,再采用阶跃响应命令。
对单位斜坡输入,由于R(s) =1/s^2,所以
其求解方法与上文中 获得冲激响应的另一种方法相同。
在状态空间中定义的系统的单位斜坡响应。
对以状态空间形式表示的系统,可以按照如 下方式获得单位斜坡响应。设系统的定义如下:
x = Ax + Bu
y = Cx + Du
其中u是单位斜坡函数。假设初始条件为零。
问题求解的核心是:
当初始条件为零时,单位斜坡响应是单位阶跃响应的积分。所以,单位斜坡响应可以表示为
根据这个关系,建立新的状态空间表达式。
对任意输入的响应
获得对任意输入的响应。
为了求得时不变系统对任意输入的响应,可以使用lsim命令。 下述命令:
lsim(num,den,u,t),
lsim(sys,u,t),
y = lsim(A,B,C,D,u,t),
[y,t] = lsim(sys,u,t)
lsim(A,B,C,D,u,t)
y = lsim(num,den,u,t)
y = lsim(sys,u,t)
在初始条件为零时会产生对 输入时间函数 u的响应。如果t由下式给定: t = 0:则从=0开始到t=T结束的区间内,每隔
秒计算一次响应,其中T是t的正整数倍。值得注意的是,带有左端参数的如下命令:
y = lsim(sys,u,t)
会返回输出响应y。矩阵y的各列是输出,它的行数等于t的长度。但它不绘制图形,要绘制响应曲线,必须再使用命令plot(t, y)。
如果状态空间模型的初始条件不为零,那么命令
lsim(sys,u,t,x0)
会生成系统对输入u和初始条件x0的响应,其中x0是初始状态。
还要注意的是,命令
Isim(sys1, sys2,..., u,t)
可以在同一幅图中绘制多个系统(sysl, sys2,...)的响应。
采用Isim命令求如下系统的单位斜坡响应:
即求对任意输入的响应,即将其时间信号的表达式赋给r,如r=t;
num = [1];
den = [1 1 1];
t = 0:0.1:8;
r = t;
y = lsim(num,den,r,t);
>> plot(t,r,'-',t,y,'o')
>> grid
title('Unit-Ramp Response Obtained by Use of Command "isim1"')
xlabel('t Sec')
ylabel('Unit-Ramp Input and System Output')
>> text(2.1,4.65,'Unit-Ramp Input')
>> text(4.5,2.0,'Output')绘制的曲线为:
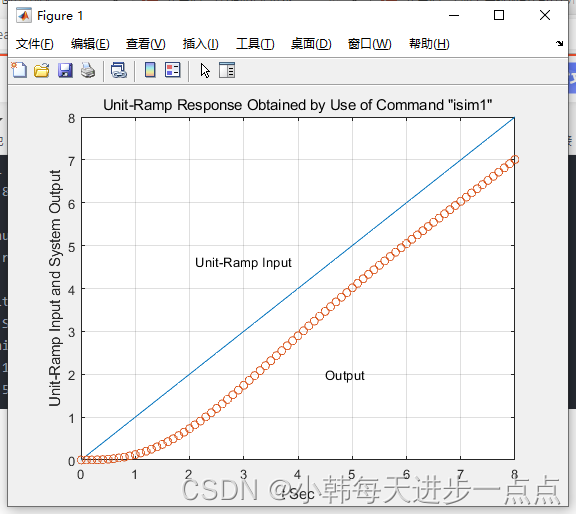
对任意初始条件的响应
拉普拉斯变换方法
我们直接看一道例题:


即根据传递函数的定义、初始条件等,改写方程来求解。
对初始条件的响应(状态空间方法,第一种情况)。


对初始条件的响应(状态空间方法,第二种情况)。

 这两种状态空间方法的情况即将系统在给定初始条件下的响应转换为求新的系统的阶跃响应。
这两种状态空间方法的情况即将系统在给定初始条件下的响应转换为求新的系统的阶跃响应。
原先的系统为:
,
新的系统为:
其中 B=x(0),u=1(t)
采用命令initial求对初始条件的响应。
如果系统以状态空间形式给出,那么命令
initial(A,B,C,D,[initial condition],t)
会生成对该初始条件的响应。
[initial condition]规定了x(0)的初始条件,见下面例题。

注意前提条件:假设不存在外力函数,即求的是零输入响应。
>> t = 0:0.05:10;
>> A = [0 1 0;0 0 1;-10 -17 -8];
>> B = [0;0;0];
>> C=[1 0 0];
>> D=[0];
>> y=initial(A,B,C,D,[2;1;0.5],t);
>> plot(t,y)
>> grid
>> title('Response to Initial Condition')
>> xlabel('t(sec)')
>> ylabel('Output y')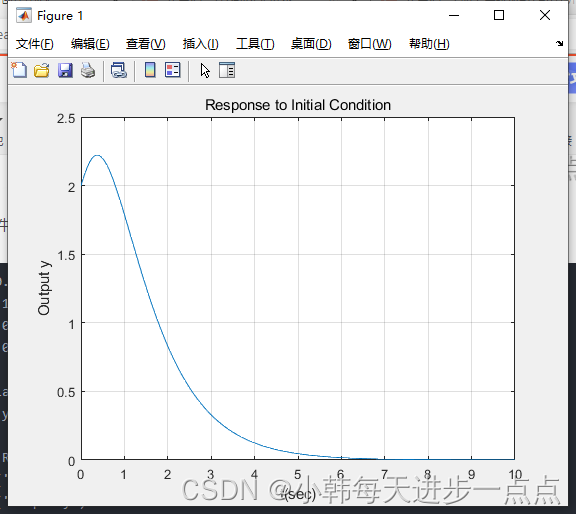
我是小韩每天进步一点点,一名研0的研究生,刚开始写博客。希望和大家多多交流,一起进步!
求朋友点赞、收藏、关注哈,鼓励一下新人博主,或者提出建议。
这篇关于瞬态响应分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!