本文主要是介绍codeforces 859E Desk Disorder,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题意:每一个人有现有的位置x[i],以及候选的位置y[i],每个人可以选择坐到现有的位置以及候选的位置,要求每个位置最多坐一个人,求合法的方案数。
我们将每一个x[i]与y[i]连一条边,那么我们可以将得到的图分成三种情况,带环的,带自环的,一棵树。
首先,我们可以证明带环的联通子图最多带一个环,因为一条边象征着一个人,一个点代表着一个座位,如果两个环的话就会出现n个点m+1条边,由于起始座位不会相同,所以有一个人会没有起始座位所以说是不合法的。对于带环的情况,我们考虑一个人,如果他坐了自己的现有位置,那么其他人n-1个人位置便固定了,所以它有两种不同的位置,所以对于有环的情况,答案就是2种。
接着考虑到带自环的情况,其实就是有环的特殊情况,相当于一个人座位一已经固定了, 其他人选的位置也就随之固定了,因为一样不会出现多环,所以答案是1种。
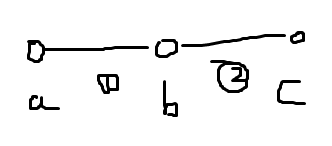
最复杂的是一个树的情况,我们可以首先从链的情况入手,如果是两个点一条边,那么它的答案就是2,这个人可以坐任何一边,如果是三个点两条边的链,如下图
如果1号人选了左边的a点,那么2号人就出现了像之前叙述的情况,共有两种情况,如果1号人选了b点,那么另外一个人选的点就固定了,那么a点的答案就是1+b点的答案,以此类推,对于一条链就是cnt[i]=cnt[i-1]+1。
我们将这种链的情况推广的树上,那么就是从根开始,如果第一条边选了向叶子的方向,那么其他点方案固定,如果选了最顶的方向,其他下面便不是固定的了,就是加上cnt[叶子节点的方案数],推一下发现答案就是一棵树的节点个数。所以树的答案就是树的节点个数。
由于各个联通子图相互独立,所以各个联通子图的答案相乘即为最终答案。
下附AC代码。
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define maxn 1000005
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
int n;
int fa[maxn],huan[maxn],zihuan[maxn],siz[maxn];
int find(int now)
{return fa[now]==now ? now : fa[now]=find(fa[now]);
}
int main()
{scanf("%d",&n);for(int i=1;i<=2*n;i++){fa[i]=i;siz[i]=1;}for(int i=1;i<=n;i++){int x,y;scanf("%d%d",&x,&y);int x1=find(x),y1=find(y);if(x==y)zihuan[x1]=1;if(x1==y1)huan[y1]=1;fa[x1]=y1;}for(int i=1;i<=2*n;i++){int x=find(i);if(x!=i){siz[x]+=siz[i];huan[x]|=huan[i];zihuan[x]|=zihuan[i];}}ll ans=1;for(int i=1;i<=2*n;i++){if(find(i)==i){if(zihuan[i]) continue;else if(huan[i]) ans=(ans*2)%mod;else ans=(ans*siz[i])%mod;}}printf("%I64d\n",ans);
} 这篇关于codeforces 859E Desk Disorder的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!