c语言函数解题思路,八年级数学备考：用真题详细解说函数题的解题思路，提高期末成绩...

点击右上角关注“良师益友谈育儿”分享学习经验，一起畅游快乐的学习生活。

一次函数和反比例函数是八年级数学的重要知识点，也是初中数学函数的基础知识，本文就例题详细讲解函数相关题型的解题思路，希望能给大家期末复习备考提供帮助。

例题1

双曲线在y=5/x第一象限的一支上有一点C(1，5)，过点C的直线y=kx＋b(k<0)与x轴交于点A(a，0)。

(1)求点A的横坐标a与k之间的函数关系式；

(2)当该直线与双曲线在第一象限内的另一交点D的横坐标是9时，求△COD的面积。

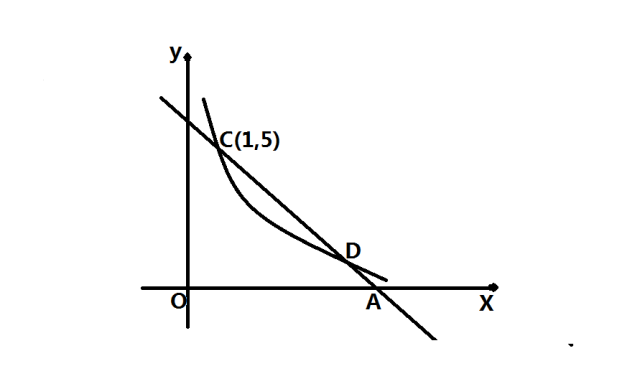
1、求a与k之间的函数关系式

根据题目中的条件：C(1，5)在直线y=kx＋b上，则C点坐标代入直线的解析式能使等式成立：5=k+b，即b=5-k。

根据题目中的条件：A(a，0)在直线y=kx＋b上，则A点坐标代入直线的解析式能使等式成立： ak+b=0。

根据结论：b=5-k，ak+b=0，则ak+5-k=0，即a=-5/k+1。

2、求△COA的面积

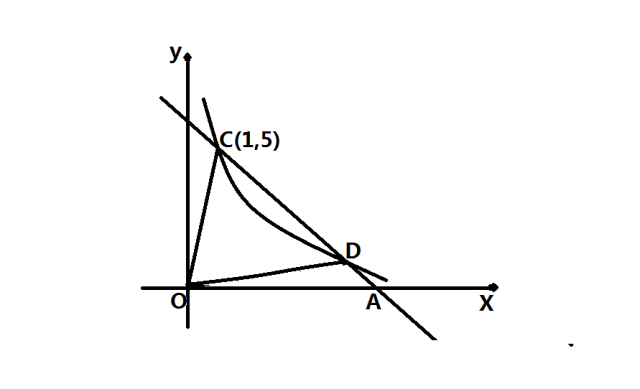
根据题目中的条件：点D在双曲线y=5/x上，点D的横坐标是9，则D点横坐标代入双曲线的解析式可以求解D点的纵坐标为5/9，即D点坐标为(9,5/9)。

根据题目中的条件：点D在直线y=kx＋b上，D点坐标为(9,5/9)，则D点坐标代入直线的解析式能使等式成立：5/9=9k+b。

根据结论：b=5-k，5/9=9k+b，则k=-5/9，b=50/9。

根据结论：a=-5/k+1，k=-5/9，则a=10，即A点坐标为(10,0)。

根据三角形面积的计算公式和结论：S△COA=OA*h/2，S△COA=OA*h’/2，h=5，h’=5/9，OA=10，则S△COA=25，S△DOA=25/9。

根据题目中的条件和结论：S△COD=S△COA-S△DOA，S△COA=25，S△DOA=25/9，则S△COD =200/9。

例题2

如图，△OAB、△ADC是等腰直角三角形，点B、C在函数y=4/x(x>0)的图象上,斜边OA、AD都在x轴上，求点D的坐标。

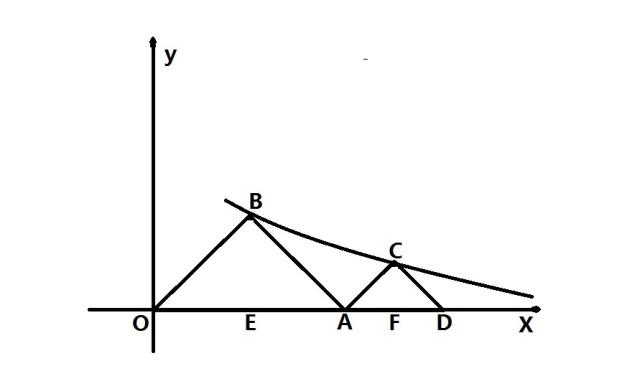
1、求B点坐标

设B点横坐标为x1，过B点作BE⊥OA，交OA于点E。

根据题目中的条件：点B在双曲线y=4/x上，B点横坐标为x1，则B点横坐标代入双曲线的解析式可以求解B点的纵坐标为4/x1，即B点坐标为(x1,4/x1)。

根据等腰直角三角形的性质和题目中的条件：等腰直角三角形斜边上的高等于斜边的一半，△OAB是等腰直角三角形，BE⊥OA，OE= x1，BE=4/x1，则OE=BE， 即x1=4/x1，解得：x1=2，所以B点坐标为(2,2)。

2、求C点坐标

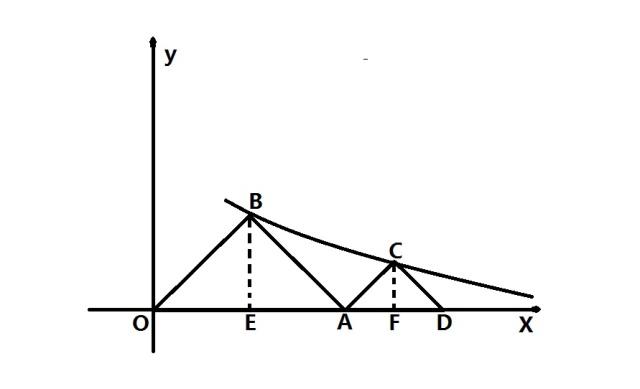
设C点横坐标为x2，过C点作CF⊥OD，交OD于点F。

根据等腰三角形三线合一的性质、题目中的条件和结论：△OAB是等腰三角形，BE⊥OA，OE=2，则OA=2OE=4。

参照第一题的做法：C点坐标为(x2,4/x2)。

根据题目中的条件和结论：OF=x2，OA=4，AF=OF-OA，则AF= x2-4。

根据等腰直角三角形的性质和题目中的条件和结论：等腰直角三角形斜边上的高等于斜边的一半，△CAD是等腰直角三角形，CF⊥OD，CF=4/x2，AF= x2-4，则CF=AF，即4/x2 = x2-4，则解得：x2=2+2√2或2-2√2。

根据题目中的条件：双曲线上的点的横坐标满足条件：x>0，则x2=2-2√2<0不符合条件，舍去，所以，x2=2+2√2。

所以C点坐标为(2+2√2，2√2-2)。

3、求D点坐标

根据等腰三角形三线合一的性质、题目中的条件和结论：△ACD是等腰三角形，CF⊥AD，OF=2+2√2，则FD=AF=2√2-2。

根据结论：OF=2+2√2，FD=2√2-2，OD= OF+ FD，则OD=4√2， 所以D点坐标为(4√2，0)。

结语

一次函数与反比例函数的解题步骤如下：

利用条件中函数图像上点的坐标，求解函数的解析式；

利用函数解析式，求解函数图像上其他点的坐标；

把点的坐标值与几何图形中的线段长度联系起来进行解题。

举报/反馈