周赛365（前后缀分解 + 枚举、滑动窗口、子数组最大和问题、内向基环树）

本文主要是介绍周赛365（前后缀分解 + 枚举、滑动窗口、子数组最大和问题、内向基环树），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

周赛365

2873. 有序三元组中的最大值 I

输入：nums = [12,6,1,2,7]
输出：77
解释：下标三元组 (0, 2, 4) 的值是 (nums[0] - nums[2]) * nums[4] = 77 。
可以证明不存在值大于 77 的有序下标三元组。

输入：nums = [1,10,3,4,19]
输出：133
解释：下标三元组 (1, 2, 4) 的值是 (nums[1] - nums[2]) * nums[4] = 133 。
可以证明不存在值大于 133 的有序下标三元组。 

输入：nums = [1,2,3]
输出：0
解释：唯一的下标三元组 (0, 1, 2) 的值是一个负数，(nums[0] - nums[1]) * nums[2] = -3 。因此，答案是 0 。

2874. 有序三元组中的最大值 II

输入：nums = [12,6,1,2,7]
输出：77
解释：下标三元组 (0, 2, 4) 的值是 (nums[0] - nums[2]) * nums[4] = 77 。
可以证明不存在值大于 77 的有序下标三元组。

输入：nums = [1,10,3,4,19]
输出：133
解释：下标三元组 (1, 2, 4) 的值是 (nums[1] - nums[2]) * nums[4] = 133 。
可以证明不存在值大于 133 的有序下标三元组。 

输入：nums = [1,2,3]
输出：0
解释：唯一的下标三元组 (0, 1, 2) 的值是一个负数，(nums[0] - nums[1]) * nums[2] = -3 。因此，答案是 0 。

前缀极值 + 枚举（枚举k）

class Solution {/* (nums[i] - nums[j]) * nums[k] 1. 记录 pre[i] 表示 i位置前缀 最大值2. 记录 pre2[i] 表示 i位置 nums[i] - nums[j] 的最大值3. 枚举 i */public long maximumTripletValue(int[] nums) {int n = nums.length;int[] pre = new int[n+1];for(int i = 0; i < n; i++){pre[i+1] = Math.max(pre[i], nums[i]);}// nums[i] - nums[j] : maxint[] pre2 = new int[n+1];for(int i = 1; i < n; i++){pre2[i+1] = Math.max(pre2[i], pre[i] - nums[i]);}long res = 0;for(int i = 0; i < n; i++){res = Math.max(res, (long)pre2[i] * (long)nums[i]);}return res;}
}

前后缀分解（枚举j）

class Solution {public long maximumTripletValue(int[] nums) {int n = nums.length;int[] sufmax = new int[n+1];for(int i = n-1; i >= 0; i--){sufmax[i] = Math.max(sufmax[i+1], nums[i]);}long ans = 0;int premax = nums[0];for(int j = 1; j < n-1; j++){ans = Math.max(ans, (long)(premax - nums[j]) * sufmax[j+1]);premax = Math.max(premax, nums[j]);}return ans;}
}

2875. 无限数组的最短子数组

输入：nums = [1,2,3], target = 5
输出：2
解释：在这个例子中 infinite_nums = [1,2,3,1,2,3,1,2,...] 。
区间 [1,2] 内的子数组的元素和等于 target = 5 ，且长度 length = 2 。
可以证明，当元素和等于目标值 target = 5 时，2 是子数组的最短长度。

输入：nums = [1,1,1,2,3], target = 4
输出：2
解释：在这个例子中 infinite_nums = [1,1,1,2,3,1,1,1,2,3,1,1,...].
区间 [4,5] 内的子数组的元素和等于 target = 4 ，且长度 length = 2 。
可以证明，当元素和等于目标值 target = 4 时，2 是子数组的最短长度。

输入：nums = [2,4,6,8], target = 3
输出：-1
解释：在这个例子中 infinite_nums = [2,4,6,8,2,4,6,8,...] 。
可以证明，不存在元素和等于目标值 target = 3 的子数组。

子数组问题（化为前缀和）

class Solution {/*1. 若 target > sum(nums) ，则需要target 减到 小于 sum(nums)2. **元素和** 等于 `target` 的 **最短** 子数组pre[r] - pre[l] = target==> 两数之和*/public int minSizeSubarray(int[] nums, int target) {int n = nums.length;int[] arrs = new int[n * 2];for(int i = 0; i < 2 * n; i++){arrs[i] = nums[i % n];}long sum = 0;int res = Integer.MAX_VALUE, diff = 0;for(int num : nums) sum += num;if(sum < target){diff += (target / sum) * n;target -= (target / sum) * sum;}if(target == 0) return diff;long[] pre = new long[n * 2 + 1];for(int i = 0; i < 2 * n; i++){pre[i+1] = pre[i] + arrs[i];}Map<Long, Integer> map = new HashMap<>();for(int i = 1; i <= 2 * n; i++){long arr = pre[i];if(map.containsKey(arr - target)){res = Math.min(res, i - map.get(arr - target));}// [left, right)map.put(arr, i);}return res == Integer.MAX_VALUE && target != 0 ? -1 : res + diff;}
}

滑动窗口

class Solution {/**滑动窗口从target中去掉若干个 sum(nums)剩余元素之和为 target % sum(nums)只需要再 nums + nums 中找一个最短子数组，作为剩余元素*/public int minSizeSubarray(int[] nums, int target) {long total = 0;for(int x : nums) total += x;int n = nums.length;int ans = Integer.MAX_VALUE;int left = 0;long sum = 0;for(int right = 0; right < n * 2; right++){sum += nums[right % n];while(sum > target % total){sum -= nums[left++ % n];}if(sum == target % total)ans = Math.min(ans, right - left + 1);}return ans == Integer.MAX_VALUE ? -1 : ans + (int)(target / total) * n;}
}

2876. 有向图访问计数

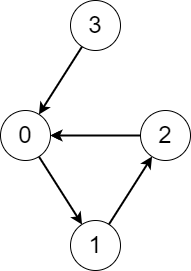
输入：edges = [1,2,0,0]
输出：[3,3,3,4]
解释：从每个节点开始执行该过程，记录如下：
- 从节点 0 开始，访问节点 0 -> 1 -> 2 -> 0 。访问的不同节点数是 3 。
- 从节点 1 开始，访问节点 1 -> 2 -> 0 -> 1 。访问的不同节点数是 3 。
- 从节点 2 开始，访问节点 2 -> 0 -> 1 -> 2 。访问的不同节点数是 3 。
- 从节点 3 开始，访问节点 3 -> 0 -> 1 -> 2 -> 0 。访问的不同节点数是 4 。

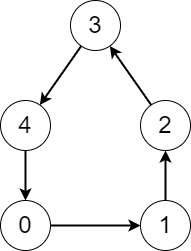
输入：edges = [1,2,3,4,0]
输出：[5,5,5,5,5]
解释：无论从哪个节点开始，在这个过程中，都可以访问到图中的每一个节点。

内向基环树

class Solution {/**对于在基环上的点，其可以访问到的节点数，就是基环的大小对于不在基环上的点x，其可以访问到的节点数，是基环大小 + x的深度（反图）*/public int[] countVisitedNodes(List<Integer> edges) {int[] g = edges.stream().mapToInt(i -> i).toArray();int n = g.length;List<Integer>[] rg = new ArrayList[n]; // rg 反图Arrays.setAll(rg, e -> new ArrayList<>());int[] deg = new int[n];for(int x = 0; x < n; x++){int y = g[x];rg[y].add(x);deg[y]++;}// 拓扑排序，剪掉 g 上的所有树枝// 拓扑排序后，deg 值为 1 的点必定在基环上，为 0 的点必定在树枝上Deque<Integer> dq = new ArrayDeque<>();for(int i = 0; i < n; i++){if(deg[i] == 0)dq.add(i);}while(!dq.isEmpty()){int x = dq.poll();int y = g[x];if(--deg[y] == 0)dq.add(y);}// 根据题目要求，收集答案// 如果要遍历基环，可以从拓扑排序后入度为 1 的节点出发，在图上搜索；// 如果要遍历树枝，可以以基环与树枝的连接处为起点，顺着反图来搜索树枝（搜索入度为 0 的节点），从而将问题转化成一个树形问题。int[] ans = new int[n];for(int i = 0; i < n; i++){if(deg[i] <= 0){continue;}// ring保存基环上的点List<Integer> ring = new ArrayList<>();for(int x = i; ; x = g[x]){deg[x] = -1; // 将基环上的点的入度标记为 -1，避免重复访问ring.add(x); // 收集在基环上的点if(g[x] == i)break;}// 遍历树枝,收集答案for(int r : ring){rdfs(r, ring.size(), rg, deg, ans); // 为方便计算，以 ring.size() 作为初始深度}}return ans;}private void rdfs(int x, int depth, List<Integer>[] rg, int[] deg, int[] ans){ans[x] = depth;for(int y : rg[x]){if(deg[y] == 0){ // 树枝上的点在拓扑排序后，入度均为 0rdfs(y, depth + 1, rg, deg, ans);}}}
}

这篇关于周赛365（前后缀分解 + 枚举、滑动窗口、子数组最大和问题、内向基环树）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！