Kotlin Monad的学习

本文主要是介绍Kotlin Monad的学习，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 前言

在学习函数式编程时，函子(Funtor)、单子(Monad) 是非常难啃的骨头，它们来自于数学范畴论，又在 Haskell 这种满是学术气息的语言上发展。

我阅读了多篇关于介绍 Monad 的文章，发现要了解它，一定要具备相关的抽象代数、范畴等知识，显然我没有这么多时间去学习这对我来说很“偏门”的知识。在浅浅的学习过程中，我发现它更接近于一种设计思想。

对我帮助最大的是 arrow-kt 框架中对于 monad 概念的阐述，而且是从 Kotlin 出发的， 文章链接：arrow对 Monad 的介绍， 本篇文章就是基于我对这位大佬所写精华的学习以及总结。

1. 一些数学概念（该小节可以跳过）

单子起源于数学，这里简单的将一些其数学概念列举出来，可以做了解，没有学习的必要性。

1.1 半群 与 幺半群

有这么一门门数学分支，叫 抽象代数，它里面有一个概念叫 半群（semi-group），半群是一个二元运算的代数系统，概念如下：

存在一个非空集合 S
存在两个 S 上的数 a, b。 定义一个二元运算 ○, 使得  a ○ b = c ， c 也在 S 集合中。对于任意 x 、 y 、z ∈ S，如果满足结合律 (x ○ y) ○ z = x ○ (y ○ z)
则称 (S, ○) 为半群  ，简称 S

半群有一个延展概念 ---- 幺半群（monoid），是一个存在单位元（幺元）的半群。 它除了满足半群的特性，还自带了另一个特性：

对于半群 (S, ○)
如果存在一个 e ∈ S， 使得 a ○ e = e ○ a = a
称三元组 (S, ○, e) 为幺半群

举个例子，比如(N+, * , 1) 就是一个幺半群， 范围是正整数，二元运算是
乘法操作满足结合律，而且任意正整数乘1都等于本身， 同理还有 (N, + , 0) 这些。

1.2 范畴、态射 与 同态

范畴可以用下面有向图表示：

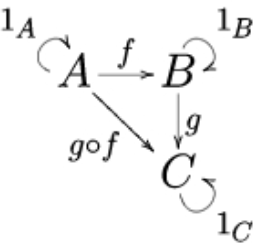
A、B、C分别是一个对象，它们通过箭头，组成了一个范畴。
范畴(category) 是一种包含了对象及对象之间箭头的代数结构， 范畴满足三个特性：

1. 对象之间的箭头可以复合
   例如有 f：A -> B 、g: B -> C，那么它们可以复合成： g ○ f: A -> C
2. 对象的箭头复合是满足结合律的
   例如有 f：A -> B 、g: B -> C、h: C -> D ，满足 ： (f ○ g) ○ h = f ○ (g ○ h)
3. 每个对象都有自己一个单位箭头
   就是每个对象都有一个单位元素，简单来说，在对象A中，存在单位元 idA 使得 A中任意元素a，有 a ○ idA = a

而 态射（morphism）的定义是两个数据结构的之间保持结构的一种过程抽象，简单来说，就是上图中的箭头。
态射听起来和映射差不多，如果你不是严格主义者，那么可以将它们理解成一个东西。在集合论中，态射就是函数！

我们定义一个态射 f: X -> Y ，如果态射满足 f(a * b) = f(a) * f(b)，那么称这个态射是一个同态。
什么意思，其实不难理解， 因为态射是两种对象间的映射，所以需要用同态来保证这个对象不会变成另外的对象，不然就把这个对象映射到其他范畴里面去了。
简单的来说，态射是一个广泛的、一般性的概念， 而同态则是一个具体的概念， 群结构上的态射都是同态的，因为我们最后还是会回到幺半群上研究问题，所以我们可以认为同态就是态射。

最后我们发现，范畴的特性和幺半群的特性存在相似之处，实际上： 幺半群实质上是只有单个对象的范畴

1.3 函子 与 自函子

函子（Funtor） 就是同态！！！

自函子则是一个能将范畴映射到自身的函子。
例如存在自函子 f 和 范畴 ob( C )， 满足 ：f : ob(C) -> ob(C)

1.4 Monad

最后再来理解 Monad 的官方定义

A Monad is just a monoid in the category of endofunctors.
Monad 不过是一个自函子范畴上的幺半群罢了

撇开定语， Monad 是一个 幺半群。

2. Monad 的一个模型

根据数学中的 Monad 特性： 结合律、 单位律，我们将 Monad 抽象成一个模型：一个盒子

1. 这个盒子里面可以装有对象
2. 这个盒子也可以是空的，但并不是什么都没有的空，而是有一个 unit 单位值 （单位律的体现）， 这种现象叫业务空值， 例如：乘法里的1， 加法里的0
3. 这个盒子可以输入一个函数进去， 它能作用到盒子里面的对象去， 函数的作用无非是 A -> B，所以盒子里面的对象会被作用，然后将结果输出出来
4. 这个盒子不仅可以输入一个函数， 还可以输入若干个函数进去，函数会复合（结合律的体现）然后应用到盒子里的对象上，最终输出一个结果

薛定谔的猫，大家应该是耳熟能详了，我们只知道这个盒子里面装了一个类型的对象，但是不知道这个对象具体是什么，我们对这个盒子施加了多个操作，最后它定能输出一个结果给我们。

3. Kotlin 中的 Monad

下面将用代码来解释 Monad 模型

3.1 一段代码

下面用 演讲者（Speak）、演讲（Conference）来举个例子

class Speaker {fun nextTalk(): Talk = TODO()
}class Talk {fun getConference(): Conference = TODO()
}class Conference {fun getCity(): City = TODO()
}class City 

我们的函数是输入一个 Speak，然后获取其演讲的 City

fun nextTalkCity(speaker: Speaker): City {val talk = speaker.nextTalk()val conf = talk.getConference()val city = conf.getCity()return city
}

这样的代码，上一行的输出是下一行的输入，所以可以优化成这样：

fun nextTalkCity(speaker: Speaker): City =speaker.nextTalk().getConference().getCity()

这段代码很美好，因为可读性高且简洁。

但是在实际开发环境中，我们不太可能写出这样的代码，因为可能会有异常情况。

3.2 考虑异常情况

考虑到属性为空的情况，如下情况：

class Speaker {fun nextTalk(): Talk? = null
}class Talk {fun getConference(): Conference? = null
}class Conference {fun getCity(): City? = null
}

那么代码就变成了：

fun nextTalkCity(speaker: Speaker?): City? =speaker?.nextTalk()?.getConference()?.getCity()

虽然能够达到目的，并且代码也足够简洁，但是多了三个额外的 ?， 怎么样才能去除这几个烦人的东西呢？

通常情况下，可以引入 Either，包装获取的数据：

object NotFoundclass Speaker {fun getTalk(): Either<NotFound, Talk> = Left(NotFound)
}class Talk {fun getConference(): Either<NotFound, Conference> = Left(NotFound)
}class Conference {fun getCity(): Either<NotFound, City> =Left(NotFound)
}

这样我们可以使用 flatmap 来处理：

fun cityToVisit(speaker: Speaker): Either<NotFound, City> =speaker.getTalk().flatMap { talk -> talk.getConference() }.flatMap { conf -> conf.getCity() }> 换个写法：
fun cityToVisit(speaker: Speaker): Either<NotFound, City> =speaker.getTalk()           .flatMap { x -> x.getConference()    }.flatMap { x -> x.getCity()         }

我们把右边蒙蔽起来，就是一开始的模样了。

解决了问题后，我们看下另外一种情况，即并行的情况

3.3 并行回调

如果我们的方法需要做一些网络请求或者读取数据库，该怎么办呢？幸运的是， Kotlin 提供了 suspend 挂起函数，可以解决嵌套的问题。

使用 suspend 来进行并行的操作，如下所示：

class Speaker {suspend fun nextTalk(): Talk = TODO()
}class Talk {suspend fun getConference(): Conference = TODO()
}class Conference {suspend fun getCity(): City = TODO()
}

调用：

suspend fun nextTalkCity(speaker: Speaker): City =speaker.nextTalk().getConference().getCity()

这样一来，挂起函数让我们又写出了简单、易读的代码。

3.4 抽象工作流

这几段代码，其实存在了一个模式。
我们在将 T? 、 Either<E, T> 、suspend () -> T 加入到工作流中，为了代码更加舒展。

我们可以把这一个工作流的过程抽象，比如 第一步是 nextTalk，第二步 getConference， 第三步 getCity，它们这些方法其实都是对一开始的数据 speaker 进行顺序处理， 然后输出一个数据，我们可以建模一个数据流处理类 WorkflowThatReturns<T>，

class WorkflowThatReturns<T> {fun addStep(step: (T) -> WorkflowThatReturns<U>): WorkflowThatReturns<U>
}

可以用下图概括：

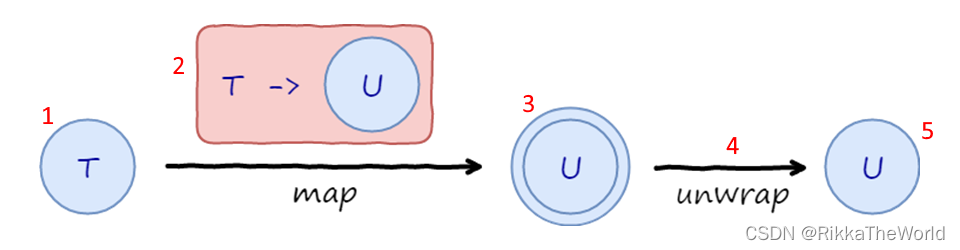
然后我们获取 city 的代码可以写成：

fun workflow(speaker: Speaker): WorkflowThatReturns<City> {returnspeaker.nextTalk().addStep { x -> x.getConference() }.addStep { x -> x.getCity() }
}

我们通过两次 addStep ，在 step 中一次调用了 getConference 和 getCity，最终获取 City 的包装类。

如下图所示：

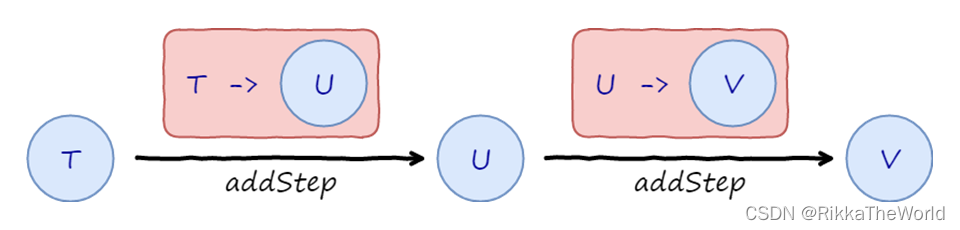
3.5 Monad

在 FP 工程环境中， 上面这种工作流模式就是 Monad！。这和我们第二节提到的盒子模型类似，最初它只是一个类型数据，然后通过一些函数操作，最终可以得到任意类型的结果数据。

4. Option、Either、Result

当我们解开了 Monad 的面纱，我们会发现它并不难理解，我们甚至能在代码中找到它的身影。

Option、Either、Result 都能体现出 Monad ！不了解的同学可以看下之前的文章：Kotlin 异常处理之 Option、Either、Result

对于 Option 来说，它封装了一个数据， 这个数据可能是 有值 或者 无值， Option 可以处理很多事情， 例如 map、 flatmap、filter， 它都体现了 Monad 的思想：

1. 封装数据到一个计算环境中， 外界能够输入函数，对“盒子”中的数据进行计算，最后得到结果
2. 它内部对异常进行处理， 在使用 Option 时，不会产生异常，所以它屏蔽了 Exception 这个副作用
3. 提供了 map、flatmap，进行数据态射

这么一看， Monad 是一个设计模式，它对数据进行封装。把 Option 是一个盒子， Result 是一个盒子， 是非常形象的。

5. Effect — 协程版本的 Either

我们可以使用 Option 、Result 来展现 Monad 思想，除此之外， arrow-kt 框架还定义了协程版本的 Either，那就是 Effect.kt， 它是一个专门用在 协程、挂起函数上的，因为上面关于 Speaker 的示例代码，我们了解了 suspend 的方式可以减小 flatmap 带来的理解负担，所以 suspend 是 Monad 发挥的极佳环境， arrow-kt 对协程上面做了很多的封装，致力帮助我们写出 FP 风格的代码。

Effect类型：

// 泛型<R> 用于表示异常， 泛型A 用于表示成功 。
public interface Effect<R, A> {public suspend fun <B> fold(recover: suspend (shifted: R) -> B,  // 失败情况下的回调transform: suspend (value: A) -> B   // 成功情况下的回调): B
...
}

并且定义了 effect 代码块，它继承 Effect，代码中将会更多的用到这个代码块：

public inline fun <R, A> effect(crossinline f: suspend EffectScope<R>.() -> A): Effect<R, A> =object : Effect<R, A> {override suspend fun <B> fold(recover: suspend (R) -> B, transform: suspend (A) -> B): B =suspendCoroutineUninterceptedOrReturn { cont ->val token = Token()val effectScope =object : EffectScope<R> {override suspend fun <B> shift(r: R): B = throw Suspend(token, r, recover as suspend (Any?) -> Any?)}try {suspend { transform(f(effectScope)) }.startCoroutineUninterceptedOrReturn(FoldContinuation(token, cont.context, cont))} catch (e: Suspend) {if (token == e.token) {val f: suspend () -> B = { e.recover(e.shifted) as B }f.startCoroutineUninterceptedOrReturn(cont)} else throw e}}}

5.1 简单示例

假设我们需要从目标路径的文件下读内容，我们首先要验证路径的正确性，这里仅做简单的判断内容，那么函数如下所示：

object EmptyPath
fun readFile(path: String): Effect<EmptyPath, Unit> = effect {  // 1、2if (path.isEmpty()) shift(EmptyPath)   // 3else Unit 
}

代码解析：

1. readFile 接收一个 String，返回一个 Effect 类型， 失败时是一个 EmptyPath 类型，成功则是 Unit
2. 使用 effect{...} 来构造，它是实现 Effect 的函数体，便于我们创建 Effect
3. shift(R) 用于快速生成一个 Suspend ，它继承自 Exception，这里用 EmptyPath 去包装。 如果传入路径是无内容的，则生成这个数据类型。 关于异常捕获，可以详看上面 effect的实现，这里不多做介绍了

if else 语句可能会产生嵌套，手动调用 shift 来创建一个Error数据可能会产生重复工作，所以Effect 还帮我们封装了一些 DSL，例如 ensureNotNull、ensure，我们来写第二个读取函数：

fun readFile2(path: String?): Effect<EmptyPath, Unit> = effect {ensureNotNull(path) { EmptyPath }     // 当 path 为空时，会调用代码块里面产生一个 Error 的数据ensure(path.isEmpty()) { EmptyPath }   // 当 path.isEmpty 为 true 时，会调用代码块里面产生一个 Error 的数据
}

最后，如果路径没有问题，我们可以把内容读取出来， Effect 的成功内容可以定义为一个 Content，并且对错误数据补充，函数如下所示：

@JvmInline
value class Content(val body: List<String>) // 文件内容sealed interface FileError  // 定义失败的情况
@JvmInline value class SecurityError(val msg: String?) : FileError
@JvmInline value class FileNotFound(val path: String) : FileError
object EmptyPath : FileError {override fun toString() = "EmptyPath"
}fun readFile(path: String?): Effect<FileError, Content> = effect {ensureNotNull(path) { EmptyPath }ensure(path.isNotEmpty()) { EmptyPath }try {val lines = File(path).readLines()Content(lines)} catch (e: FileNotFoundException) {shift(FileNotFound(path))} catch (e: SecurityException) {shift(SecurityError(e.message))}
}

验证：

   // 这里的 shoubleBe 使用到了 KotestreadFile("").toEither() shouldBe Either.Left(EmptyPath)readFile("knit.properties").toValidated() shouldBe  Validated.Invalid(FileNotFound("knit.properties"))readFile("gradle.properties").toIor() shouldBe Ior.Left(FileNotFound("gradle.properties"))readFile("README.MD").toOption { None } shouldBe None

像 toEither、 toValidataed 这些就是定义的一些扩展函数，比较简单的，你也可以自定义

5.2 处理异常

Effect 定义了协议异常处理，这和别的异常处理框架相似，都有像 handleError、 handleErrorWith、redeem 函数，如下

val failed: Effect<String, Int> =effect { shift("failed") }val resolved: Effect<Nothing, Int> =failed.handleError { it.length }val newError: Effect<List<Char>, Int> =failed.handleErrorWith { str ->effect { shift(str.reversed().toList()) }}val redeemed: Effect<Nothing, Int> =failed.redeem({ str -> str.length }, ::identity)val captured: Effect<String, Result<Int>> =effect<String, Int> { 1 }.attempt()suspend fun main() {failed.toEither() shouldBe Either.Left("failed")resolved.toEither() shouldBe Either.Right(6)newError.toEither() shouldBe Either.Left(listOf('d', 'e', 'l', 'i', 'a', 'f'))redeemed.toEither() shouldBe Either.Right(6)captured.toEither() shouldBe Either.Right(Result.success(1))
}

5.3 配合 withContext

有了 Effect 后，我们可以将其运用到各种使用到协程的场合了，例如

suspend fun main() {val exit = CompletableDeferred<ExitCase>()effect<FileError, Int> {withContext(Dispatchers.IO) {val job = launch { awaitExitCase(exit) }val content = readFile("failure").bind()  // 如果shift 被调用，会取消 withContextjob.join()content.body.size}}.fold({ e -> e shouldBe FileNotFound("failure") }, { fail("Int can never be the result") })exit.await().shouldBeInstanceOf<ExitCase>()
}

这里不再介绍 Effect，大家有兴趣可以去看官方文档。

总结

• Monad 来源于数学，发展于FP， 在实际工程中，它指的是一个工作流模型，能够对源数据进行操作，最终输出结果。
• Result、Either、Option 都能体现 Monad 的思想
• Effect 是 Arrow 框架对 Monad 的定义的接口，可以通过实现该接口来达到达到 Monad

参考

Kotlin 版图解 Functor、Applicative 与 Monad
函数式编程（四）：函数组合、函子
幺半群
详解函数式编程之Monad
范畴

这篇关于Kotlin Monad的学习的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---